UP DELED 1st Semester Math Question Paper 2025 आप यहां से प्राप्त कर सकते हैं। जिसका कोई भी शुल्क आपसे नही लिया जाएगा, आप आसानी से इसे हल कर सकेंगे । आइए विस्तार से सभी प्रश्नो को जानें –
प्रश्न-पुस्तिका
प्रथम सेमेस्टर-2025
चतुर्थ प्रश्न-पत्र
(गणित)
1. सभी प्रश्न अनिवार्य हैं। प्रत्येक प्रश्न के निर्धारित अंक प्रश्न के सम्मुख दिये गये हैं।
2. इस प्रश्न-पत्र में तीन प्रकार के (वस्तुनिष्ठ, अतिलघु उत्तरीय तथा लघु उत्तरीय) प्रश्न हैं। वस्तुनिष्ठ प्रश्नों के सही विकल्प छाँटकर अपनी उत्तर पुस्तिका में लिखें। अति लघु उत्तरीय प्रश्नों के उत्तर लगभग तीस (30) शब्दों में, लघु उत्तरीय प्रश्नों के उत्तर लगभग पचास (50) शब्दों में लिखिए।
वस्तुनिष्ठ प्रश्न
1. समद्विबाहु समकोण त्रिभुज में न्यूनकोणों का योग होता है-
(1) 45° (2) 90°
(3) 180° (4) 60°
Ans. (2) 90°
2. संख्या 2515 में अंक 5 के स्थानीय मानों का अन्तर है-
(1) 510 (2) 505
(3) 490 (4) 495
Ans. (4) 495
3. 3/5 को प्रतिशत में बदलने पर मान होगा-
(1) 30% (2) 50%
(3) 60% (4) 80%
Ans. (3) 60%
4. (3a + 2b + 5) – (2a – 3b + 2) को सरल करने पर प्राप्त मान होगा-
(1) a + 5b + 3 (2) 5a – b + 7
(3) a + b + 3 (4) a – b + 3
Ans. (1) a + 5b + 3
5. 36 और 42 का महत्तम समापवर्तक होगा –
(1) 12 (2) 6
(3) 252 (4) 2
Ans. (2) 6
अति लघु उत्तरीय प्रश्न
6. -7/25 + 4/5 + 2/5 को सरल कीजिए। –
Ans. 4/5+2/5 =6/5 = 30/25
⇒ −7/25+30/25 = 23/25
7. वृहत्कोण किसे कहते हैं?
Ans. वह कोण जो समकोण (90°) से बड़ा पर पूर्ण कोण (180°) से छोटा हो — अर्थात 90° < वृहत् कोण < 180° (अर्थात obtuse angle)।
8. दो संख्याओं का गुणनफल 1050 है। यदि उन संख्याओं का महत्तम समापवर्तक 5 है, तो ल.स. ज्ञात कीजिए।
Ans. दिया है:
दो संख्याओं का गुणनफल = 1050
दोनों संख्याओं का महत्तम समापवर्तक (HCF) = 5
हम जानते हैं कि—HCF×LCM=दो संख्याओं का गुणनफल
इसलिए,
⇒ अतः दोनों संख्याओं का ल.स. (LCM) = 210
9. एक आयताकार खेत का क्षेत्रफल 120 वर्ग मीटर है। यदि खेत की लम्बाई 40 मीटर हो, तो चौड़ाई ज्ञात कीजिए।
Ans. आयताकार खेत का क्षेत्रफल (Area) दिया है:
लम्बाई (Length) दी है:
हम जानते हैं—
इसलिए,
⇒ अतः खेत की चौड़ाई = 3 मीटर
10. एक गाँव की कुल जनसंख्या 2000 है। 15 वर्ष तक की आयु वाले बालकों तथा बालिकाओं की संख्या क्रमशः 30% एवं 25% है। बालक तथा बालिकाओं की संख्या ज्ञात कीजिए।
Ans. कुल जनसंख्या = 2000
बालकों की संख्या (30%)
बालिकाओं की संख्या (25%)
⇒ बालकों की संख्या = 600
⇒ बालिकाओं की संख्या = 500
11. यदि किसी वर्गाकार मैदान की प्रत्येक भुजा 25 मीटर है, तो इसके चारों ओर दो बार तार लगाने के लिए कितने मीटर तार की आवश्यकता होगी?
Ans. वर्गाकार मैदान की एक भुजा = 25 मीटर
1. मैदान की परिमाप (Perimeter)
वर्ग की परिमाप =
2. दो बार तार लगाने के लिए कुल तार
⇒ आवश्यक कुल तार = 200 मीटर
लघु उत्तरीय प्रश्न
12. यदि a = 2, b = 1 तथा c = 3 हो, तो (2a + 4b – c) 3 का मान ज्ञात कीजिए ?
Ans. दिया है:
व्यंजक:
पहले कोष्ठक के अंदर का मान निकालते हैं —
अब जोड़-घटाव करें —
अब पूरे मान का घन करें —
⇒ अन्तिम उत्तर = 125
13. पटरी और परकार की सहायता से 120° का कोण बनाइए।
Ans.
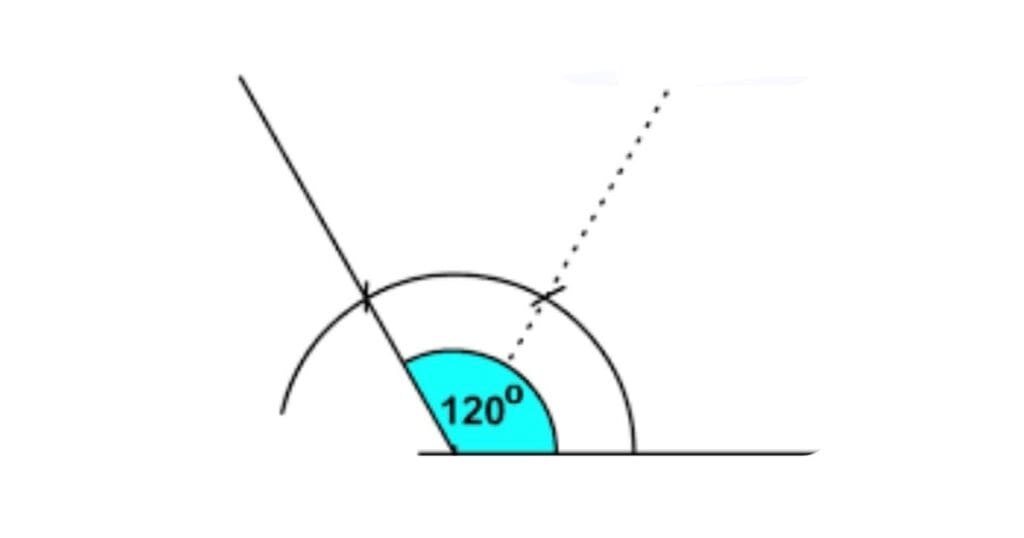
14. नीचे दिए गए त्रिभुज के तीनों अन्तः कोणों का मान अलग-अलग ज्ञात कीजिए।
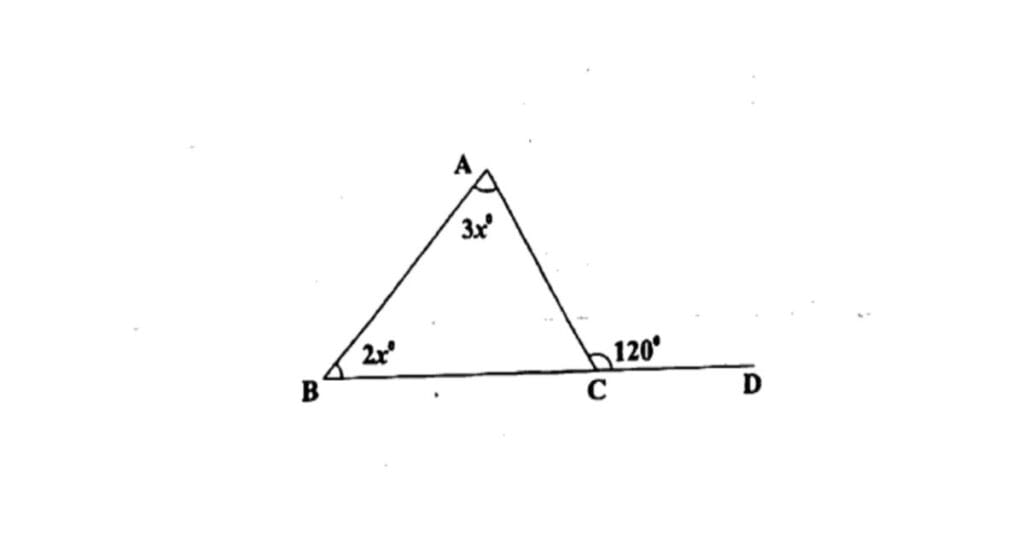
Ans. चित्र में त्रिभुज ABC दिया है।
बिन्दु C पर त्रिभुज के बाहरी कोण का मान 120° दिया है।
हम जानते हैं:
बाहरी कोण = उससे सटे हुए दो अन्तः कोणों का योग
अर्थात्
चित्र से:
इसलिए
अब तीनों कोण निकालते हैं—
1. कोण A
2. कोण B
3. कोण C (अन्तः कोण)
बाहरी कोण = 120°
बाहरी + आन्तरिक = 180° (सीधी रेखा)
इसलिए
15. बगल में दिया गया दण्ड आरेख किसी आवासीय विद्यालय के विद्यार्थियों की संख्या दर्शाता है।
दण्ड आरेख के आधार पर निम्नलिखित प्रश्नों के उत्तर दीजिए:
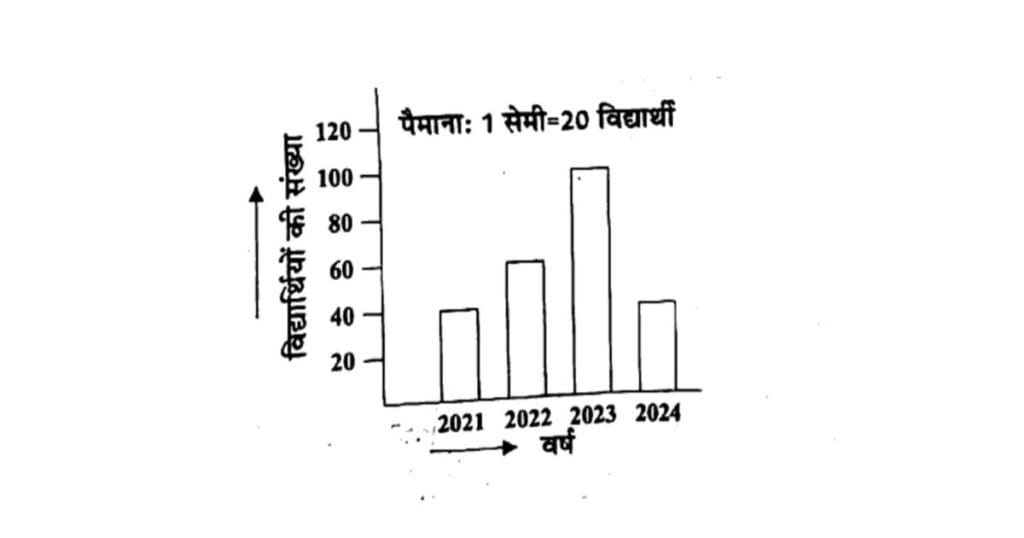
(1) 2022 में विद्यार्थियों की संख्या कितनी है?
Ans. 2022 का स्तम्भ 60 के स्तर तक जाता है।
पैमाना: 1 सेमी = 20 विद्यार्थी
तो
अर्थात् विद्यार्थियों की कुल संख्या 60 है।
✔ 2022 में विद्यार्थियों की संख्या = 60
(2) अधिकतम विद्यार्थियों की संख्या किस वर्ष में है?
Ans. दण्ड आरेख में सबसे ऊँचा स्तम्भ 2023 का है, जो लगभग 100 विद्यार्थियों तक जाता है।
16. सरल कीजिए: -12+(-6)+2-[(-5)*(-4)-{2 – (3 – 5)}]
Ans. स्टेप–1: अंदर से हल करें
(3 – 5) = -2
अब
स्टेप–2: गुणा हल करें
अब कोष्ठक बनेगा:
स्टेप–3: कोष्ठक हल करें
अब मुख्य अभिव्यक्ति:
स्टेप–4: सभी को जोड़-घटाएँ
पहले जोड़ते हैं:
✔ अंतिम उत्तर : -32
17. एक व्यक्ति अपनी आय का 1/4भाग मकान बनवाने में, 1/5 भाग बच्चों की शिक्षा में तथा भाग अन्य मदों में खर्च करता है। आय का कौन सा भाग व्यक्ति के पास बचता है? प्रतिशत में भी बचा भाग ज्ञात कीजिए।
Ans. दिया हुआ :
एक व्यक्ति अपनी आय का
- भाग मकान पर,
- भाग बच्चों की शिक्षा पर,
- भाग अन्य मदों पर खर्च करता है।
(1) कुल खर्च = ?
सभी खर्चों को जोड़ते हैं :41+51+61
इनका LCM = 60
अब भिन्नों को 60 के हर में बदलते हैं—41=6015,51=6012,61=6010
अब जोड़ते हैं—
(2) व्यक्ति के पास बचा हुआ भाग = ?
✔ बचा हुआ आय का भाग =
(3) प्रतिशत में बचा भाग = ?
✔ बचा प्रतिशत = 38.33%
18. एक शहर की जनसंख्या 2001 में 5,17,524 थी। सन् 2011 में जनसंख्या 6,46,905 हो गयी। जनसंख्या में कितने प्रतिशत की वृद्धि हुई?
Ans. 2001 की जनसंख्या = 5,17,524
2011 की जनसंख्या = 6,46,905
वृद्धि = 6,46,905 − 5,17,524 = 1,29,381
अब प्रतिशत वृद्धि:
⇒ जनसंख्या में 25% की वृद्धि हुई।
