बल आघूर्ण (Moment of Force or Torque)

यदि किसी पिण्ड को किसी एक बिन्दु या अक्ष पर स्थिर कर दिया जाए और उस पिण्ड पर ऐसा बल लगाया जाए जिसकी क्रिया-रेखा उस स्थिर बिन्दु या अक्ष से होकर न गुज़रे, तो पिण्ड उस बिन्दु या अक्ष के परितः घूमने लगता है।
बल द्वारा किसी पिण्ड को किसी बिन्दु अथवा अक्ष के परितः घुमाने की प्रवृत्ति को बल-आघूर्ण कहते हैं।

बल-आघूर्ण का मान लगाए गए बल के परिमाण पर तथा घूर्णन अक्ष से बल की क्रिया-रेखा की लंबवत दूरी पर निर्भर करता है।

$$\text{बल-आघूर्ण} = बल \times लंबवत दूरी$$

या$$\tau = F \times r$$

जहाँ,
$F$= लगाया गया बल
$r$ = अक्ष से बल की क्रिया-रेखा की लंबवत दूरी

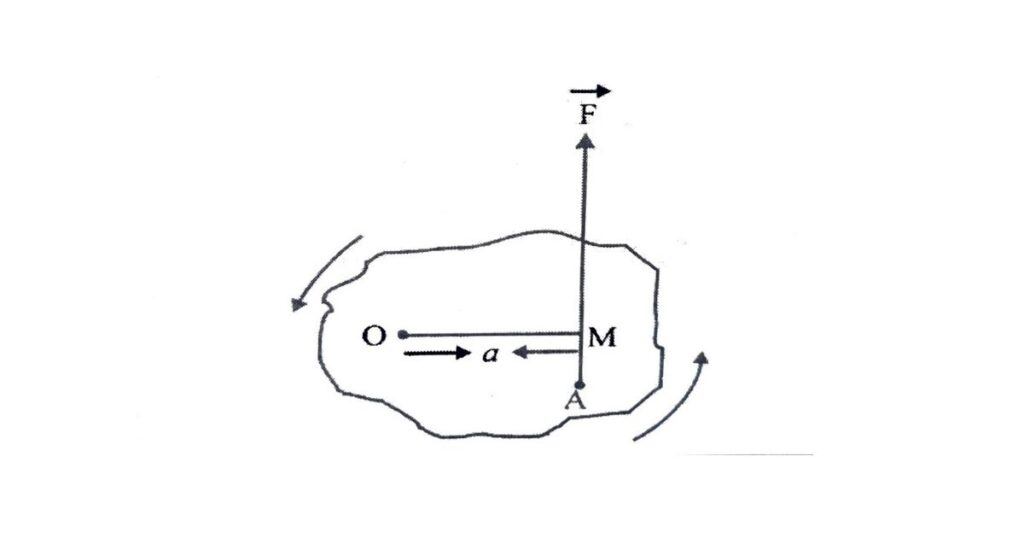
बल आघूर्ण की माप (Measurement of Torque)

किसी अक्ष या बिन्दु के परितः किसी बल का बल-आघूर्ण, उस बल के परिमाण तथा अक्ष से बल की क्रिया-रेखा के बीच की लंबवत दूरी के गुणनफल के बराबर होता है।

$$\tau = F \times d$$

जहाँ,
$\tau$ = बल-आघूर्ण
$F$ = लगाया गया बल
$d$ = बल-बाहु (अक्ष से बल की क्रिया-रेखा की लंबवत दूरी)

प्रकृति :

⦿ बल-आघूर्ण एक सदिश राशि होती है।
⦿ (विशेष रूप से इसे अक्षीय सदिश / Axial Vector कहा जाता है।)

मात्रक : बल-आघूर्ण का SI मात्रक न्यूटन-मीटर (N m) होता है।

बल आघूर्ण का लाभ (Benefit of Torque)

बल-आघूर्ण के सिद्धान्त के अनुसार, यदि आघूर्ण भुजा (बल-बाहु) की लंबाई बढ़ा दी जाए, तो वही कार्य कम बल लगाकर किया जा सकता है।
अर्थात्,$$\tau = F \times d$$

यदि $d$ अधिक होगा तो आवश्यक $F$ कम होगा।

उदाहरण :
घर में गेहूँ पीसने के लिए उपयोग किए जाने वाले जाँते (Quern) का हत्था कील (अक्ष) से काफी दूर लगाया जाता है, ताकि जाँते को घुमाने के लिए कम बल लगाना पड़े।
इसी प्रकार, पानी निकालने वाले हैंड-पम्प का हत्था लंबा बनाया जाता है जिससे कम प्रयास में अधिक कार्य किया जा सके।

सरल एवं जटिल मशीनों में उपयोग

इसी सिद्धान्त के आधार पर अनेक सरल मशीनों तथा जटिल मशीनों का निर्माण किया गया है, जैसे—

1. उत्तोलक (Lever)
2. घिरनी (Pulley)
3. आनत तल (Inclined Plane)
4. स्क्रू जैक (Screw Jack)

आघूर्णों का सिद्धान्त (Principle of Moments)

यदि किसी पिण्ड पर कई बल आरोपित हों जो उसे किसी स्थिर बिन्दु या अक्ष के परितः घुमाने की प्रवृत्ति रखते हों और इसके बावजूद वह पिण्ड स्थिर अवस्था में रहे, तो पिण्ड घूर्णन संतुलन की अवस्था में होता है।

इस स्थिति में उस अक्ष के परितः सभी बलों के आघूर्णों का बीजीय योग शून्य होता है।

अर्थात्,

वामावर्ती (Anticlockwise) आघूर्णों का योग = दक्षिणावर्ती (Clockwise) आघूर्णों का योग

$$\sum \tau = 0$$

मान लीजिए XY एक समान मोटाई की छड़ है जो O बिन्दु पर आलम्ब (Fulcrum) पर टिकी हुई है।
छड़ के विभिन्न बिन्दुओं A, B, C तथा D पर क्रमशः
$\vec{F}_1, \vec{F}_2, \vec{F}_3$​ तथा $\vec{F}_4$​ बल (या भार) लगाए गए हैं।

यदि छड़ संतुलन में है, तो—$$(+F_1 \times d_1) + ( +F_2 \times d_2) + ( -F_3 \times d_3) + ( -F_4 \times d_4) = 0$$

या,$$F_1 d_1 + F_2 d_2 = F_3 d_3 + F_4 d_4$$​

जहाँ,
$d_1, d_2, d_3, d_4$​ = अक्ष O से संबंधित बलों की आघूर्ण भुजाएँ हैं।

बलयुग्म (Couple Force)

यदि किसी वस्तु पर दो बराबर, समानांतर तथा विपरीत दिशा में कार्य करने वाले बल लगाए जाएँ, जिनकी क्रिया-रेखाएँ भिन्न हों, तो वे वस्तु को घुमाने का प्रयत्न करते हैं, परंतु उसका स्थानांतरण (Translation) नहीं करते।
इस प्रकार के बलों के जोड़े को बल-युग्म (Couple) कहते हैं।

विशेषताएँ

1. दोनों बल परिमाण में बराबर होते हैं।
2. दोनों बल दिशा में विपरीत होते हैं।
3. दोनों बल समानांतर होते हैं।
4. बलों की क्रिया-रेखाएँ अलग-अलग होती हैं।
5. बल-युग्म केवल घूर्णन प्रभाव उत्पन्न करता है, स्थानांतरण नहीं।

प्रभाव (Effect)

बल-युग्म का सम्मिलित प्रभाव यह होता है कि पिण्ड को एक ही दिशा में घुमाने की प्रवृत्ति उत्पन्न होती है।
बल-युग्म का आघूर्ण शून्य नहीं होता।

दैनिक जीवन के उदाहरण

1. 🚗 गाड़ी का स्टियरिंग व्हील घुमाना
2. 🚰 पानी का नल खोलना या बंद करना
3. ⏰ घड़ी में चाबी भरना
4. 🔩 पेचकस से पेंच कसना या खोलना
5. 🫙 बोतल का ढक्कन घुमाकर खोलना

सरल मशीन (Simple Machine)

सरल मशीन वह युक्ति है जो बल-आघूर्ण के सिद्धान्त पर कार्य करती है और जिसमें किसी उपयुक्त (सुविधाजनक) बिन्दु पर थोड़ा-सा बल लगाकर किसी कार्य को अपेक्षाकृत आसानी से किया जा सकता है।

सरल मशीनें या तो

• बल की दिशा बदलती हैं,
• बल के परिमाण को बढ़ाती हैं, अथवा
• कार्य को सुविधाजनक बनाती हैं।

दैनिक जीवन के उदाहरण

1. 🪵 लट्ठे (लीवर) की सहायता से भारी लकड़ी के बोटे या पत्थर को खिसकाना।
2. 🚚 आनत तल (Inclined Plane) की सहायता से भारी वस्तुओं को ट्रक पर चढ़ाना।
3. 🔧 सरौता (Plier) की सहायता से अत्यंत कठोर सुपारी (नट) को काटना।
4. ⚖️ तराजू द्वारा वस्तुओं का भार मापना।
5. 🔩 स्क्रू जैक से भारी वाहन को ऊपर उठाना।

मशीन की दक्षता (Efficiency of Machine)

किसी मशीन को दी गई निवेशित ऊर्जा (Input Energy) और मशीन द्वारा किए गए उपयोगी कार्य या निर्गत ऊर्जा (Output Energy) के अनुपात को मशीन की दक्षता कहते हैं।

कारण (Why efficiency < 100%)

यद्यपि मशीन की सहायता से कम बल लगाकर अधिक भार उठाया जा सकता है, फिर भी मशीन को दी गई कुल ऊर्जा का कुछ भाग

• घर्षण बलों,
• ऊष्मा,
• ध्वनि आदि के रूप में व्यर्थ हो जाता है।

इसलिए—

निवेशित ऊर्जा > निर्गत ऊर्जा

इसी कारण किसी वास्तविक मशीन की दक्षता सदैव 100% से कम होती है।

पूर्ण दक्ष (आदर्श) मशीन

यदि किसी मशीन की दक्षता 100% हो, अर्थात्
निवेशित ऊर्जा = निर्गत ऊर्जा
तो ऐसी मशीन को पूर्ण दक्ष (Perfectly Efficient) या आदर्श (Ideal) मशीन कहते हैं।
(व्यवहार में ऐसी मशीन संभव नहीं है।)

(1) सामान्य सूत्र :

$$\text{दक्षता} = \frac{\text{मशीन द्वारा किया गया कार्य}}{\text{मशीन को दी गई ऊर्जा}} \times 100$$

(2) यांत्रिक राशियों के रूप में :

$$\text{दक्षता (प्रतिशत में)} = \frac{\text{यांत्रिक लाभ (Mechanical Advantage)}}{\text{वेग अनुपात (Velocity Ratio)}} \times 100$$

Note : किसी भी वास्तविक मशीन की दक्षता 100% नहीं हो सकती।

यह भी पढ़ें : संवेग (Momentum)