द्रव स्थैतिकी (Hydrostatics)

भौतिक विज्ञान की वह शाखा है, जिसके अंतर्गत स्थिर अवस्था में स्थित द्रवों के सामान्य गुण-धर्मों तथा द्रवों के भीतर उत्पन्न बल, दाब और तरल पदार्थों पर कार्य करने वाले बलों के कारण होने वाली संतुलन अवस्था का अध्ययन किया जाता है।

➤ पदार्थ (Matter)

प्रत्येक वह वस्तु जिसमें द्रव्यमान होता है, जो स्थान घेरती है तथा जिसका अनुभव हम अपनी ज्ञानेंद्रियों द्वारा कर सकते हैं, द्रव्य कहलाती है।
जैसे—लोहा, हवा, पानी, लकड़ी, दूध आदि।

द्रव्य की मुख्यतः तीन अवस्थाएँ पाई जाती हैं—

1. ठोस (Solid)
2. द्रव (Liquid)
3. गैस (Gas)

इसके अतिरिक्त द्रव्य की एक और अवस्था पाई जाती है जिसे प्लाज्मा (Plasma) कहते हैं। यह द्रव्य की सामान्य अवस्था नहीं है तथा यह केवल अत्यधिक उच्च ताप एवं दाब पर ही प्राप्त होती है। यह अवस्था प्रायः सूर्य तथा पृथ्वी के केंद्रीय भाग में पाई जाती है।

➤ पदार्थों के सामान्य गुण (General Properties of Matter)

पदार्थों के प्रमुख सामान्य गुण निम्नलिखित हैं—

1. अवस्था परिवर्तन (Change of State)
2. प्रत्यास्थता (Elasticity)
3. दाब (Pressure)
4. प्लवन (Floating)
5. पृष्ठ तनाव (Surface Tension)
6. केशिकत्व (Capillarity)
7. श्यानता (Viscosity)

यहाँ हम द्रव्य के उपर्युक्त गुणों का अध्ययन ठोस (Solids), द्रव (Liquids) एवं गैसों (Gases) में अलग-अलग करेंगे।

➤ ठोस (Solid)

ठोस पदार्थ की वह अवस्था है जिसमें सामान्य परिस्थितियों में पदार्थ का आकार एवं आयतन दोनों निश्चित होते हैं। ठोस पदार्थ आकार तथा आयतन में होने वाले परिवर्तनों का विरोध करता है।

➤ द्रव (Liquid)

द्रव पदार्थ की वह अवस्था है जिसमें पदार्थ आकार में परिवर्तन का विरोध नहीं करता तथा जिस पात्र में रखा जाता है, उसी का आकार ग्रहण कर लेता है, परंतु उसका आयतन निश्चित रहता है।

➤ गैस (Gas)

गैस पदार्थ की वह अवस्था है जिसमें पदार्थ का आकार एवं आयतन दोनों अनिश्चित होते हैं। गैस को जिस पात्र में रखा जाता है, वह उसी का आकार एवं आयतन ग्रहण कर लेती है।

दाब (Pressure)

यदि किसी सतह पर उसके लम्बवत् कोई बल लगाया जाए, तो कहा जाता है कि उस सतह पर दाब लग रहा है। किसी पृष्ठ (सतह) पर लगने वाला दाब, उस पर आरोपित बल तथा पृष्ठ के क्षेत्रफल के अनुपात के बराबर होता है।
अतः एकांक क्षेत्रफल पर कार्यरत बल को दाब कहते हैं।

दाब एक अदिश राशि (Scalar Quantity) है।

गणितीय सूत्र

$$\text{दाब (P)} = \frac{\text{पृष्ठ के लम्बवत् बल (F)}}{\text{पृष्ठ का क्षेत्रफल (A)}}$$

दाब के मात्रक (Units of Pressure)

(a) न्यूटन प्रति वर्ग मीटर (N/m²) या पास्कल (Pa)
SI पद्धति में दाब का मात्रक पास्कल (Pa) है।$$1 \, \text{Pa} = 1 \, \text{N/m}^2$$

(b) पारे का सेंटीमीटर (cm of Hg)
यह वह दाब है जो किसी तल पर स्थित 1 सेमी ऊँचे पारे के स्तम्भ द्वारा आरोपित किया जाता है। इसका प्रयोग द्रवों एवं गैसों के दाब को व्यक्त करने में किया जाता है।$$1 \, \text{सेमी पारा} = 1.33 \times 10^3 \, \text{N/m}^2$$$$76 \, \text{सेमी पारा} = 1.013 \times 10^5 \, \text{N/m}^2$$

इसे 1 वायुमण्डलीय दाब (1 atm) कहते हैं।

सामान्यतः दाब को केवल सेमी या मिमी में लिखा जाता है, परंतु उसका अर्थ सेमी पारा या मिमी पारा ही होता है।
जब वायुदाब को 76 सेमी या 760 मिमी कहा जाता है, तो इसका अर्थ है कि वायुमण्डल का दाब सतह पर 76 सेमी ऊँचे पारे के स्तम्भ के बराबर है।

(c) बार (Bar) एवं मिलीबार (Millibar)
मौसम विज्ञान (Meteorology) में वायुमण्डलीय दाब को प्रायः बार या मिलीबार में व्यक्त किया जाता है।$$1 \, \text{बार} = 10^5 \, \text{N/m}^2 = 10^5 \, \text{Pa}$$ $$1 \, \text{मिलीबार} = 10^2 \, \text{N/m}^2 = 10^2 \, \text{Pa}$$

वायुमण्डलीय दाब:$$1 \, \text{atm} = 1.013 \, \text{बार} = 1013 \, \text{मिलीबार}$$

(d) टॉर (Torr)$$1 \, \text{टॉर} = 1 \, \text{मिमी पारा} = 133.8 \, \text{Pa}$$

यदि चाहें तो मैं इसे अति संक्षेप नोट्स, तालिका के रूप में मात्रकों की तुलना, या कक्षा 9/10 की परीक्षा हेतु आदर्श उत्तर के रूप में भी तैयार कर सकता हूँ।

➤ द्रवदाब (Pressure In Liquids)

द्रवों के अणु (molecules of liquids) इतने स्वतंत्र होते हैं कि वे द्रव की सीमा के भीतर विभिन्न दिशाओं में निरंतर अनियमित गति (Random Motion) करते रहते हैं। इस कारण वे आपस में तथा पात्र की दीवारों से लगातार टकराते रहते हैं। परिणामस्वरूप द्रव के भीतर सभी दिशाओं में बल आरोपित होता है।
द्रव द्वारा प्रति इकाई क्षेत्रफल पर लगाए गए इसी बल को द्रव का दाब कहते हैं।

चूँकि द्रव के अणु सभी दिशाओं में समान रूप से गति करते हैं, अतः द्रव के किसी भी बिंदु पर दाब सभी दिशाओं में समान रूप से कार्य करता है।

द्रव दाब का सूत्र

द्रव के भीतर किसी बिंदु पर दाब की गणना निम्न सूत्र से की जाती है—$$P = h \times d \times g$$

जहाँ—

• $h$ = द्रव की सतह से उस बिंदु की गहराई
• $d$ = द्रव का घनत्व (Density)
• $g$ = गुरुत्वीय त्वरण

द्रव दाब पर निर्भरता

द्रव का दाब निर्भर करता है—

1. द्रव के घनत्व पर
2. द्रव की सतह से गहराई पर
3. गुरुत्वीय त्वरण पर

परंतु द्रव का दाब द्रव की आकृति या पात्र की आकृति पर निर्भर नहीं करता।

कुल द्रव दाब

यदि द्रव के स्वतंत्र तल पर लगने वाले वायुमण्डलीय दाब को भी सम्मिलित कर लिया जाए, तो द्रव में किसी बिंदु पर कुल दाब—$$\text{कुल दाब} = \text{वायुमण्डलीय दाब} + h d g$$

➤ द्रव दाब के नियम (Laws of Liquid Pressure)

(1) द्रव के भीतर किसी बिन्दु पर द्रव का दाब द्रव के स्वतंत्र तल से बिंदु की गहराई पर निर्भर करता है। जैसे-जैसे गहराई बढ़ती है, द्रव का दाब भी बढ़ता है।

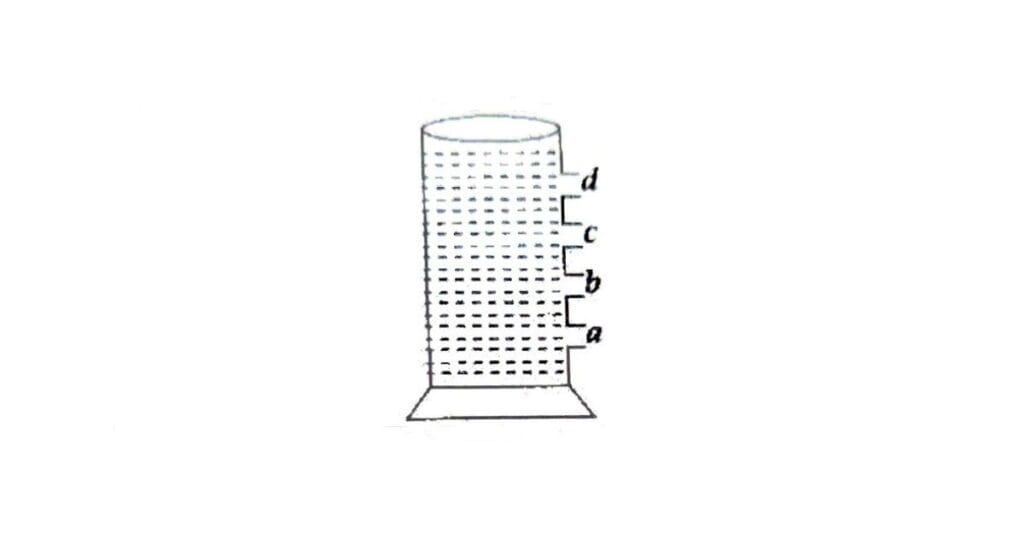
चित्रानुसार जैसे-जैसे गहराई बढ़ रही है पात्र के छिद्र से निकलने वाली धारा अधिक दूर (a के द्वारा) जाकर गिर रही है अर्थात् गहराई बढ़ने पर दाब बढ़ रहा है।

(2) एक ही गहराई पर द्रव का दाब चारों ओर समान होता है।*

चित्रानुसार, यदि किसी बर्तन में चारों तरफ छेद कर दिया जाय तो चारों ओर पानी समान दाब से निकलता प्रतीत होता है क्योंकि पानी की धारा पृथ्वी पर बराबर दूरी पर जाकर गिरती है।

(3) किसी द्रव के एक ही क्षैतिज तल में स्थित सभी बिंदुओं पर दाब समान होता है।*

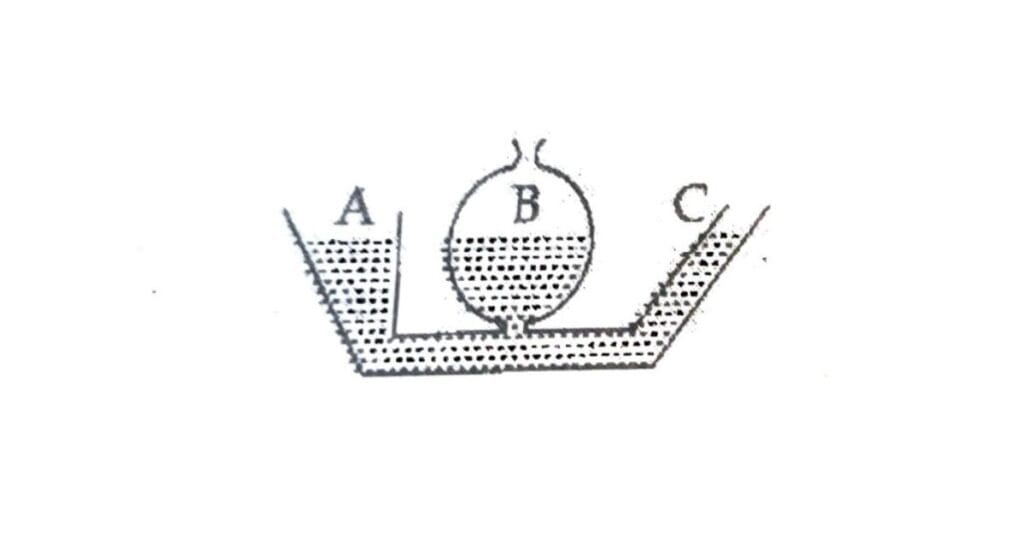
चित्र – बिंदु A, B, C व D पर दाब समान है अर्थात् द्रव पात्र में द्रव का दाब सिर्फ उसकी ऊर्ध्वाधर गहराई (h) पर निर्भर करता है यह नली के आकार या चौड़ाई पर निर्भर नहीं करता।

(4) समान गहराई पर द्रव का दाब द्रव के घनत्व पर निर्भर करता है। यदि अनेक बर्तनों में समान गहराई तक भिन्न-भिन्न द्रव भरे जायें तो जिस बर्तन में भरे द्रव का घनत्व अधिक होगा उसकी पेंदी पर द्रव का दाब भी अधिक होगा।

➤ पास्कल का नियम (Pascal’s Law)

(a) यदि गुरुत्वीय प्रभाव को शून्य मान लिया जाए, तो संतुलन की अवस्था में द्रव के भीतर प्रत्येक बिंदु पर दाब समान होता है। जब गुरुत्व बल प्रभावी होता है, तब गहराई के साथ द्रव दाब बढ़ता जाता है, परंतु समान गहराई पर स्थित सभी बिंदुओं पर द्रव दाब समान रहता है।

(b) किसी बर्तन में बन्द द्रव के किसी भाग पर आरोपित बल, द्रव द्वारा सभी दिशाओं में समान रूप से एवं बिना किसी कमी के प्रसारित कर दिया जाता है।

(c) द्रव पर लगने वाला दाब बर्तन के आकार या आकृति पर निर्भर नहीं करता, बल्कि केवल द्रव के घनत्व, गहराई तथा गुरुत्वीय त्वरण पर निर्भर करता है।

➤ गलनांक तथा क्वथनांक पर दाब का प्रभाव (Effect of Pressure on Melting and Boiling Point)

(1) गलनांक पर प्रभाव (Effect on Melting Point): जिन पदार्थों को गर्म करने पर आयतन में वृद्धि होती है, उन पर यदि दाब बढ़ाया जाए, तो उनका गलनांक बढ़ जाता है।
उदाहरण— मोम, घी आदि।

इसके विपरीत, जिन पदार्थों को गर्म करने पर आयतन में कमी आती है, उन पर दाब बढ़ाने से उनका गलनांक घट जाता है।
उदाहरण— बर्फ, बिस्मथ तथा ढलवा लोहा आदि।

(2) क्वथनांक पर प्रभाव (Effect on Boiling Point): दाब बढ़ने पर सभी द्रवों का क्वथनांक बढ़ जाता है।

उदाहरण के लिए—
साधारण जल 1 वायुमण्डलीय दाब पर 100°C पर उबलता है,
परंतु जब दाब बढ़ाकर 2 वायुमण्डलीय दाब के बराबर कर दिया जाता है, तो जल लगभग 125°C पर उबलता है।

प्लवन (Floatation)

किसी वस्तु के किसी द्रव में तैरने की घटना को प्लवन कहते हैं। प्लवन वस्तु के भार तथा द्रव द्वारा वस्तु पर लगाए गए उत्क्षेप (Upthrust) पर निर्भर करता है।

जब किसी वस्तु को किसी द्रव में डुबाया जाता है या डुबाने का प्रयास किया जाता है, तो द्रव उस वस्तु पर ऊपर की दिशा में एक बल लगाता है। इस बल का अनुभव हमें वस्तु के भार में प्रतीत होने वाली कमी के रूप में अथवा वस्तु को छोड़ देने पर उसके स्वतः ऊपर उठ आने से होता है। इस ऊपर की ओर लगने वाले बल को उत्प्लावन बल (Buoyant Force) कहते हैं।

द्रव का वह गुण, जिसके कारण वह किसी वस्तु पर ऊपर की ओर बल लगाता है, उत्क्षेप (Upthrust) कहलाता है।

जल में उत्क्षेप का अध्ययन सर्वप्रथम आर्किमिडीज (Archimedes) ने किया तथा इसके आधार पर उन्होंने एक सिद्धान्त प्रतिपादित किया, जिसे आर्किमिडीज का सिद्धान्त (Archimedes’ Principle) कहा जाता है।

➤ आर्किमिडीज का सिद्धान्त (Archimede’s Principle)

जब किसी ठोस वस्तु को किसी द्रव में पूर्णतः या अंशतः डुबाया जाता है, तो ठोस के भार में कमी प्रतीत होती है। ठोस के भार में यह कमी (जिसे आभासी कमी कहते हैं) उस ठोस द्वारा विस्थापित (हटाए गए) द्रव के भार के बराबर होती है।

अतः$$\text{उत्प्लावन बल} = \text{भार में आभासी कमी} = \text{हटाए गए द्रव का भार}$$

परिणामी बल की स्थिति

मान लें—

• ठोस का वास्तविक भार = $W$
• हटाए गए द्रव का भार = $W_1$​
  (यही उत्प्लावन बल है)

तो द्रव में ठोस पर कार्यरत परिणामी बल—$$= W – W_1$$

इस स्थिति में निम्न तीन अवस्थाएँ संभव हैं—

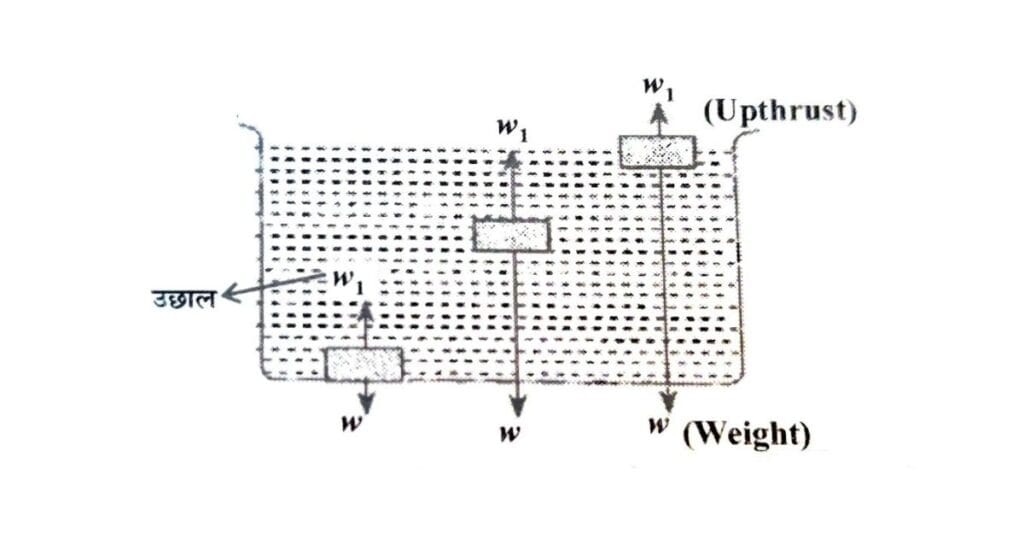
(1) जब $W > W_1$

अर्थात् वस्तु का भार उत्प्लावन बल से अधिक है,
तो परिणामी बल नीचे की ओर होगा और वस्तु डूब जाएगी।

यह स्थिति तब होती है जब—$$\text{वस्तु का घनत्व} > \text{द्रव का घनत्व}$$

(2) जब $W = W_1$

इस दशा में परिणामी बल शून्य होगा।
वस्तु पूरी तरह द्रव में डूबी हुई तैरती रहेगी।

यह तब होता है जब—$$\text{वस्तु का घनत्व} = \text{द्रव का घनत्व}$$

(3) जब $W < W_1$

अर्थात् महत्तम उत्प्लावन बल वस्तु के भार से अधिक है,
तो वस्तु को पूरी तरह डुबाकर छोड़ने पर वह ऊपर की ओर उठने लगेगी।

धीरे-धीरे वस्तु का कुछ भाग द्रव के बाहर आ जाएगा, जिससे विस्थापित द्रव का भार घटेगा और अंततः—$$W = W_1$$

इस अवस्था में वस्तु का कुछ भाग द्रव के भीतर तथा कुछ भाग द्रव की सतह के ऊपर रहेगा और वस्तु तैरेगी।

प्लवन का नियम (Law of Floatation)

तैरने की संतुलित अवस्था में वस्तु अपने भार के बराबर द्रव विस्थापित करती है।

अर्थात्—$$\text{विस्थापित द्रव का भार} = \text{वस्तु का भार}$$

आंशिक रूप से डूबी हुई तैरती वस्तु के लिए

$$\frac{\text{वस्तु का घनत्व } (d_s)}{\text{द्रव का घनत्व } (d_L)} = \frac{\text{वस्तु का डूबा हुआ आयतन } (v_1)}{\text{वस्तु का कुल आयतन } (v)}$$

यही द्रव के सापेक्ष ठोस का आपेक्षिक घनत्व (Relative Density) है।

आपेक्षिक घनत्व से प्राप्त निष्कर्ष

(a) किसी ठोस का आपेक्षिक घनत्व

$$= \frac{\text{ठोस का वायु में भार}}{\text{जल में ठोस के भार में कमी}}$$

(b) किसी द्रव का आपेक्षिक घनत्व

$$= \frac{\text{द्रव में ठोस के भार में कमी}}{\text{जल में ठोस के भार में कमी}}$$

➤ द्रव दाब व आर्किमिडीज सिद्धान्त पर आधारित विभिन्न उपकरण (Equipments based on the principle of Archimedes and Pressure of Liquid)

(1) मैनोमीटर (Manometer): मैनोमीटर को दाबांतर मापी कहते हैं। इसका उपयोग किसी बर्तन में भरी गैस के दाब को मापने के लिए किया जाता है।

यह काँच की बनी एक ‘U’ आकार की नली होती है, जिसके दोनों सिरे खुले रहते हैं। नली के निचले भाग में पारा (Hg) अथवा कोई अन्य उपयुक्त द्रव भरा जाता है। प्रारम्भ में, चूँकि दोनों नलियों पर समान वायुमण्डलीय दाब कार्य करता है, इसलिए दोनों भुजाओं में द्रव का तल समान ऊँचाई पर रहता है।

जिस बर्तन में भरी गैस का दाब ज्ञात करना होता है, उसे नली के एक सिरे से जोड़ दिया जाता है, जबकि दूसरा सिरा वायुमण्डल के लिए खुला रहता है। यदि गैस का दाब वायुमण्डलीय दाब से अधिक होता है, तो गैस की ओर वाली नली में द्रव का तल नीचे चला जाता है तथा दूसरी ओर ऊपर उठ जाता है। इसके विपरीत, यदि गैस का दाब वायुमण्डलीय दाब से कम हो, तो गैस की ओर वाली नली में द्रव का तल ऊपर उठ जाता है।

दोनों नलियों में द्रव स्तरों के बीच ऊँचाई का अंतर ही गैस के दाबांतर का माप प्रदान करता है।

(2) सरल वायुदाबमापी (Simple Barometer): यदि एक छोर से बन्द तथा दूसरे छोर से खुली, लगभग 1 मीटर लंबी और मोटी दीवार वाली काँच की नली में पारा भरकर उसे पारे से भरे एक टब में उल्टा करके ऊर्ध्वाधर स्थिति में खड़ा किया जाए, तो नली में भरा पारा कुछ नीचे उतरकर एक निश्चित ऊँचाई पर स्थिर हो जाता है।

नली में बने पारे के स्तम्भ की ऊँचाई वायुमण्डलीय दाब के अनुक्रमानुपाती होती है। अर्थात्—

• वायुमण्डलीय दाब अधिक होने पर नली में पारा ऊँचा उठता है (कम गिरता है),
• वायुमण्डलीय दाब कम होने पर पारे के स्तम्भ की ऊँचाई कम हो जाती है।

मानक स्थिति

सामान्यतः समुद्र तल पर पारे के स्तम्भ की ऊँचाई लगभग 76 सेमी होती है। जैसे-जैसे ऊँचाई (समुद्र तल से ऊपर) बढ़ती जाती है, वायुमण्डलीय दाब घटता जाता है और परिणामस्वरूप पारे के स्तम्भ की ऊँचाई भी कम होती जाती है।

इसी युक्ति को सरल वायुदाबमापी (Simple Barometer) कहते हैं।
अतः कहा जाता है कि वायुमण्डलीय दाब पारे के 76 सेमी ऊँचे स्तम्भ के दाब के बराबर होता है।

संख्यात्मक मान

$$76 \, \text{सेमी पारा} = 1.013 \times 10^5 \, \text{न्यूटन/मी}^2 = 1.013 \, \text{बार}$$

अन्य द्रवों का प्रयोग

सैद्धान्तिक रूप से पारे के स्थान पर अन्य द्रवों का भी प्रयोग किया जा सकता है, परंतु द्रव का घनत्व कम होने पर नली की लंबाई अधिक रखनी पड़ती है।

उदाहरण के लिए—
यदि पारे के स्थान पर जल का प्रयोग किया जाए, तो वायुमण्डलीय दाब को संतुलित करने के लिए नली की लंबाई लगभग 10.33 मीटर रखनी होगी।

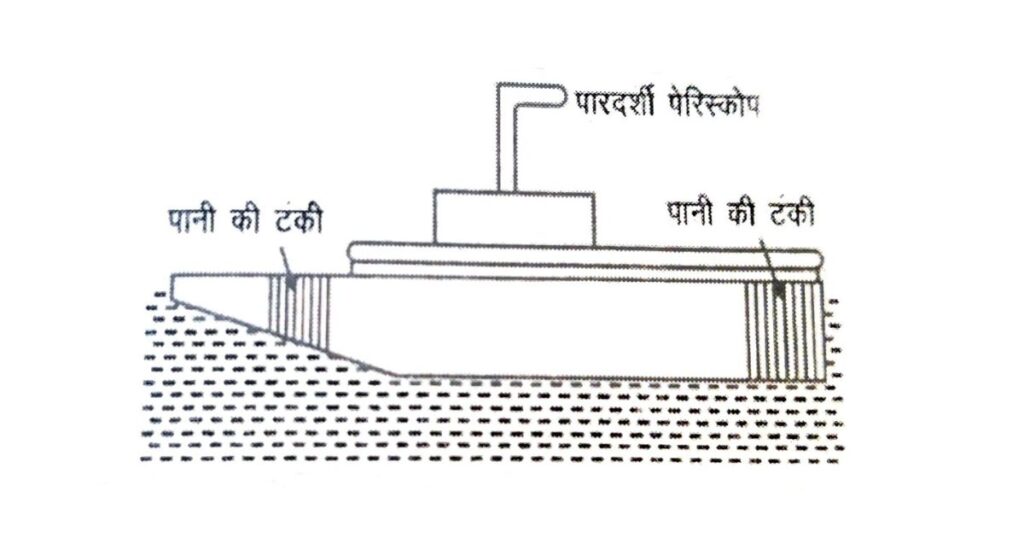
➤ पनडुब्बी (Submarine)

जल के भीतर डूबकर तथा तैरकर चल सकने वाले जलयान को पनडुब्बी (Submarine) कहते हैं। पनडुब्बी का कार्य सिद्धान्त प्लवन के नियम तथा आर्किमिडीज के सिद्धान्त पर आधारित होता है।

पनडुब्बी के आगे एवं पीछे दो बड़ी जल-टंकियाँ (Ballast Tanks) होती हैं, जिनमें पम्पों की सहायता से समुद्री जल भरा या निकाला जा सकता है। आवश्यकता के अनुसार इन टंकियों में जल की मात्रा नियंत्रित की जाती है, जिससे पनडुब्बी जल के भीतर डूबकर संतुलित अवस्था में तैर सके।

जब पनडुब्बी संतुलित अवस्था में होती है, तब उसके द्वारा विस्थापित जल का भार पनडुब्बी के भार के बराबर होता है।
यदि विस्थापित जल का भार पनडुब्बी के भार से कम हो जाता है, तो पनडुब्बी नीचे की ओर डूबने लगती है।
इसके विपरीत, यदि विस्थापित जल का भार पनडुब्बी के भार से अधिक हो जाए, तो पनडुब्बी ऊपर की ओर उठने लगती है।

इस प्रकार प्लवन के नियम के प्रयोग द्वारा पनडुब्बी को इच्छानुसार जल के भीतर अथवा जल की सतह पर संचालित किया जा सकता है।

➤ द्रव घनत्वमापी (Hydrometer)

हाइड्रोमीटर एक ऐसा यंत्र है जो आर्किमिडीज के सिद्धान्त पर कार्य करता है। इसका उपयोग द्रवों का विशिष्ट गुरुत्व (Specific Gravity / Relative Density) ज्ञात करने तथा उनकी शुद्धता (Purity) की जाँच करने के लिए किया जाता है।

जब किसी वस्तु को किसी द्रव में डाला जाता है, तो वह अपने भार के बराबर द्रव विस्थापित करती है। अधिक घनत्व वाले द्रव में वस्तु कम डूबती है, जबकि कम घनत्व वाले द्रव में वह अधिक डूबती है। इसी सिद्धान्त के आधार पर हाइड्रोमीटर द्वारा विभिन्न द्रवों के घनत्व की गणना की जाती है।

आपेक्षिक घनत्व का सूत्र

$$\text{किसी वस्तु का आपेक्षिक घनत्व} = \frac{\text{वस्तु का वायु में भार}}{\text{पानी में वस्तु के भार में कमी}}$$

यदि किसी वस्तु का आपेक्षिक घनत्व 1 होता है, तो उसका घनत्व पानी के घनत्व के बराबर होता है, अर्थात्—$$\text{पानी का घनत्व} = 1 \, \text{g/cm}^3 = 1.0 \times 10^3 \, \text{kg/m}^3$$

दुग्ध घनत्वमापी (Lactometer)

लैक्टोमीटर (Lactometer) भी हाइड्रोमीटर का ही एक प्रकार है। इसका उपयोग दूध का घनत्व मापने तथा उसमें पानी की मिलावट का पता लगाने के लिए किया जाता है।

द्रव गतिकी (Hydrodynamics)

द्रव गतिकी भौतिक विज्ञान की वह शाखा है जिसमें गतिशील द्रव पर कार्य करने वाले बल, दाब और उसकी ऊर्जा का अध्ययन किया जाता है।

ससंजक और आसंजक बल (Cohesive and Adhesive Forces)

प्रत्येक पदार्थ अणुओं (molecules) से मिलकर बना होता है, जो आपस में एक-दूसरे को आकर्षित करते हैं।

1. ससंजक बल (Cohesive Force)
   • यह बल एक ही पदार्थ के अणुओं के बीच कार्य करता है।
   • उदाहरण—पानी के अणुओं के बीच का बल।
2. आसंजक बल (Adhesive Force)
   • यह बल भिन्न-भिन्न पदार्थों के अणुओं के बीच कार्य करता है।
   • उदाहरण—पानी और काँच के अणुओं के बीच का बल।

ध्यान दें कि ये बल गुरुत्वाकर्षण बलों से भिन्न होते हैं और व्युत्क्रम वर्ग नियम (F ∝ 1/r²) का पालन नहीं करते।

ससंजक और आसंजक बल का प्रभाव

• ठोस (Solids)
  • ससंजक बल बहुत अधिक होता है।
  • अणु दृढ़ता से बंधे रहते हैं।
  • परिणाम—आकार और आयतन नियत रहते हैं।
• गैस (Gases)
  • ससंजक बल नगण्य होता है।
  • अणु स्वतंत्र रूप से गतिशील रहते हैं।
  • परिणाम—आकार और आयतन अनिश्चित होते हैं; विसरण (Diffusion) संभव है।
• द्रव (Liquids)
  • ससंजक बल ठोस से कम, गैस से अधिक होता है।
  • आयतन निश्चित रहता है, पर आकार नियत नहीं होता।
  • परिणाम—द्रव बहनीय (Flowing) होते हैं।

यह भी पढ़ें – कार्य, सामर्थ्य और ऊर्जा