द्रव का स्वतंत्र पृष्ठ सदैव तनाव की अवस्था में रहता है तथा वह न्यूनतम क्षेत्रफल प्राप्त करने की प्रवृत्ति रखता है। द्रव के पृष्ठ में उत्पन्न यही तनाव पृष्ठ तनाव कहलाता है।
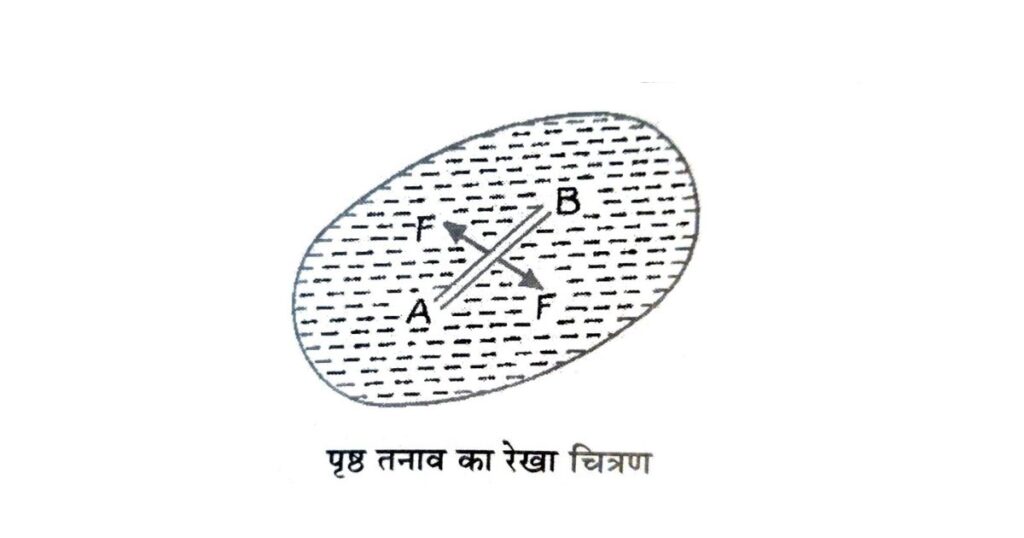
यदि किसी द्रव के पृष्ठ पर एक काल्पनिक रेखा AB खींची जाए, तो इस रेखा के दोनों ओर स्थित द्रव-पृष्ठ एक-दूसरे पर एक आकर्षण बल (Pulling Force) लगाते हैं। यह बल—
- रेखा AB के लम्बवत्
- तथा द्रव-पृष्ठ के तल के समांतर होता है।
रेखा AB की प्रति इकाई लम्बाई पर कार्य करने वाले इस बल का परिणाम ही द्रव का पृष्ठ तनाव कहलाता है।
यदि रेखा AB की लम्बाई = l
और इसके एक ओर कार्य करने वाला कुल बल = F हो,
तो पृष्ठ तनाव,
मात्रक एवं विमीय सूत्र
- SI मात्रक : न्यूटन/मीटर (N/m)
- विमीय सूत्र :
कार्य के रूप में पृष्ठ तनाव
यदि किसी द्रव के पृष्ठ के क्षेत्रफल में की वृद्धि करने के लिए W कार्य करना पड़े, तो द्रव का पृष्ठ तनाव—
यदि ,
तो
अर्थात् द्रव के पृष्ठ के क्षेत्रफल में प्रति इकाई वृद्धि करने के लिए किया गया कार्य ही पृष्ठ तनाव के बराबर होता है।
वैकल्पिक मात्रक
इस परिभाषा के कारण पृष्ठ तनाव का मात्रक—
- जूल/मीटर² (J/m²) भी होता है।
➤ पृष्ठतनाव का कारण (Reason of Surface Tension)
द्रव के सभी अणु ससंजक बल (Cohesive Force) के कारण एक-दूसरे को आकर्षित करते हैं। द्रव के भीतर स्थित किसी अणु पर चारों दिशाओं से समान आकर्षण बल कार्य करते हैं, अतः इन बलों का परिणामी बल शून्य होता है और वह अणु संतुलन की अवस्था में रहता है।
परंतु द्रव के मुक्त पृष्ठ (Free Surface) पर स्थित अणुओं की स्थिति भिन्न होती है। इन अणुओं पर—
- अगल-बगल के अणुओं द्वारा लगाए गए बल परस्पर निष्प्रभावी हो जाते हैं,
- नीचे स्थित अणुओं द्वारा लगाया गया आकर्षण बल प्रभावी रहता है,
- जबकि ऊपर की ओर कोई अणु न होने के कारण कोई बल कार्य नहीं करता।
फलस्वरूप मुक्त पृष्ठ पर स्थित सभी अणु नीचे की ओर खिंचाव अनुभव करते हैं। इसी कारण द्रव का पृष्ठ ऐसी अवस्था में रहता है मानो वह एक तनी हुई इलास्टिक झिल्ली हो, जो अपने क्षेत्रफल को न्यूनतम करने का प्रयास करती है।
इसी घटना के परिणामस्वरूप द्रव के पृष्ठ पर पृष्ठ तनाव (Surface Tension) उत्पन्न हो जाता है।
➤ पृष्ठ तनाव पर ताप तथा अशुद्धियों का प्रभाव (Effect of Temperature and Impurities on Surface Tenstion)
(1) ताप का प्रभाव
सामान्यतः ताप बढ़ाने पर द्रव के अणुओं की गतिज ऊर्जा बढ़ जाती है, जिससे उनके बीच का ससंजक बल कमजोर हो जाता है। परिणामस्वरूप द्रव का पृष्ठ तनाव कम होता जाता है।
एक निश्चित ताप जिसे क्रांतिक ताप (Critical Temperature) कहते हैं, पर द्रव का पृष्ठ तनाव शून्य हो जाता है। इस ताप पर द्रव एवं वाष्प के बीच का भेद समाप्त हो जाता है तथा द्रव को द्रवीभूत नहीं किया जा सकता।
(2) अशुद्धियों का प्रभाव
(i) घुलनशील अशुद्धियाँ
यदि किसी द्रव में मिलाई गई अशुद्धि अत्यधिक घुलनशील हो, तो द्रव का पृष्ठ तनाव बढ़ जाता है।
उदाहरण — जल में नमक मिलाने पर पृष्ठ तनाव बढ़ जाता है।
(ii) अघुलनशील या सतह-सक्रिय अशुद्धियाँ
यदि मिलाई गई अशुद्धि अघुलनशील हो, तो वह द्रव के पृष्ठ पर एकत्रित होकर उसे संदूषित (Contaminated) कर देती है। इससे द्रव के अणुओं के बीच का ससंजक बल घट जाता है और परिणामस्वरूप पृष्ठ तनाव कम हो जाता है।
उदाहरण — जल में ऐल्कोहल मिलाने पर जल का पृष्ठ तनाव कम हो जाता है।
➤ स्पर्श-कोण (Tangent Angle)
जब कोई द्रव किसी ठोस तल के संपर्क में आता है, तो द्रव का मुक्त पृष्ठ सामान्यतः क्षैतिज न होकर वक्राकार (Curved) हो जाता है। यह वक्रता द्रव तथा ठोस के बीच लगने वाले आसंजन बल और द्रव के अणुओं के बीच के ससंजक बल के कारण उत्पन्न होती है।
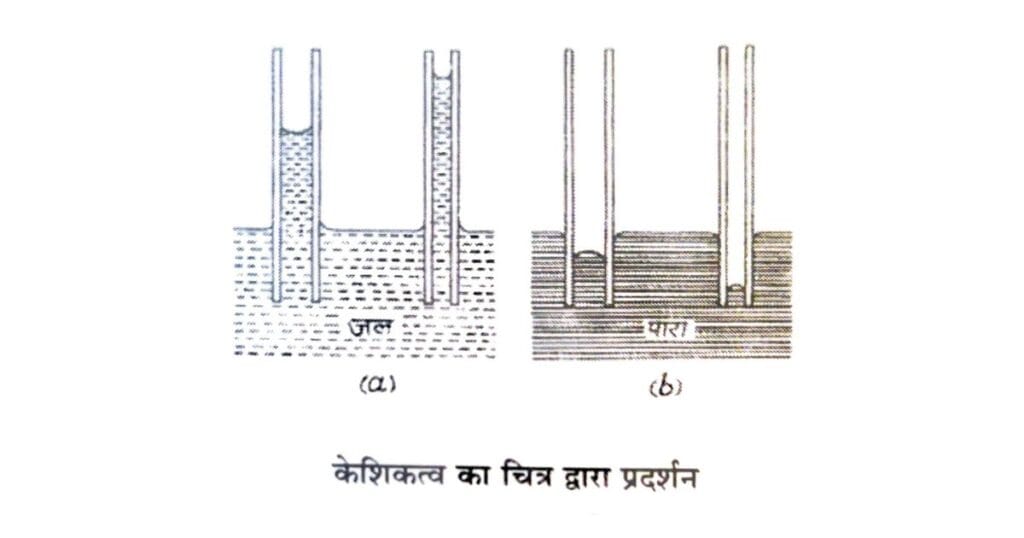
यदि दो केशनली नलिकाओं में क्रमशः जल और पारा भरा जाए, तो पाया जाता है कि—
- जल का तल अवतल (Concave) होता है,
- पारे का तल उत्तल (Convex) होता है।
द्रव के मुक्त पृष्ठ पर खींची गई स्पर्श रेखा तथा ठोस तल पर द्रव के भीतर की ओर खींची गई स्पर्श रेखा के बीच बने कोण को उस द्रव और ठोस के लिए स्पर्श कोण (Angle of Contact) कहते हैं।
स्पर्श कोण का वर्गीकरण
- भिगोने वाले द्रव (Wetting Liquids)
जो द्रव किसी ठोस को भिगोते हैं, उनका स्पर्श कोण न्यून कोण (90° से कम) होता है।
उदाहरण — जल और काँच (θ < 90°) - न भिगोने वाले द्रव (Non-wetting Liquids)
जो द्रव किसी ठोस को नहीं भिगोते, उनका स्पर्श कोण अधिक कोण (90° से अधिक) होता है।
उदाहरण — पारा और काँच (θ ≈ 135°)
विशेष उदाहरण
- काँच और पारे के लिए स्पर्श कोण का मान लगभग 135° होता है।
- जल और चाँदी के लिए स्पर्श कोण का मान 90° होता है।
इसी कारण चाँदी के बर्तन में जल का तल किनारों पर भी क्षैतिज रहता है।
केशिकत्व (Capillarity)
यदि काँच के दोनों सिरों से खुली एक केश नली (Capillary Tube) को ऐसे द्रव में खड़ा किया जाए जो काँच को भिगोता हो (जैसे— जल), तो द्रव केश नली में ऊपर चढ़ जाता है।
इसके विपरीत, यदि केश नली को ऐसे द्रव में खड़ा किया जाए जो काँच की दीवारों से न चिपकता हो (जैसे— पारा), तो नली के भीतर द्रव का तल बाहरी तल की अपेक्षा नीचे उतर जाता है।
केश नली में द्रव के ऊपर चढ़ने या नीचे उतरने की इस घटना को केशिकत्व (Capillarity) कहते हैं।
केश नली (Capillary Tube)
केश नली एक अत्यंत कम तथा समान त्रिज्या वाली खोखली काँच की नली होती है।
केश नली में द्रव का चढ़ाव या उतार—
- नली की त्रिज्या (या व्यास),
- द्रव के पृष्ठ तनाव,
- द्रव के घनत्व,
- तथा स्पर्श कोण पर निर्भर करता है।
केशिकत्व का सूत्र
यदि
- केश नली की त्रिज्या =
- द्रव का पृष्ठ तनाव =
- द्रव का घनत्व =
- गुरुत्वीय त्वरण =
- स्पर्श कोण =
तो केश नली में द्रव के चढ़ने (या उतरने) की ऊँचाई (या गहराई)—
निष्कर्ष
- जितनी कम होगी (नली जितनी पतली होगी),
→ उतना ही अधिक होगा। - जल (θ < 90°) → चढ़ाव
- पारा (θ > 90°) → उतार
कारण
केश नली में द्रव के चढ़ने या उतरने का मुख्य कारण पृष्ठ तनाव है, जो आसंजन बल और ससंजक बल के संयुक्त प्रभाव से उत्पन्न होता है।
श्यानता (Viscosity)
द्रवों का वह गुण जिसके कारण वे अपनी विभिन्न पर्तों (Layers) के बीच होने वाली आपेक्षिक गति का विरोध करते हैं, श्यानता या गाढ़ापन (Viscosity) कहलाता है।
यह द्रव की पर्तों के बीच कार्य करने वाला एक प्रकार का आंतरिक घर्षण बल है।
जिस द्रव में श्यानता का मान जितना अधिक होता है—
- उसे हिलाने या बहाने में उतना ही अधिक बल लगाना पड़ता है,
- तथा गति में लाने के बाद छोड़ देने पर वह द्रव उतनी ही शीघ्र विरामावस्था में आ जाता है।
उदाहरण:
- किसी बर्तन में रखे द्रव को बिलोकर छोड़ देने पर वह थोड़ी देर बाद स्वयं रुक जाता है। यह द्रव की श्यानता के कारण होता है।
- हम वायु में जितनी तेजी से चल सकते हैं, उतनी तेजी से जल में नहीं चल सकते, क्योंकि जल की श्यानता वायु की अपेक्षा अधिक होती है।
- बादलों के सूक्ष्म जलकण वायु की श्यानता के कारण बहुत धीरे-धीरे नीचे आते हैं, जिससे वे आकाश में तैरते हुए प्रतीत होते हैं।
श्यानता का कारण
श्यानता का गुण तरल पदार्थों (द्रव एवं गैसों) में उपस्थित ससंजक बल (Cohesive Force) के कारण उत्पन्न होता है, जो द्रव की विभिन्न पर्तों को एक-दूसरे से बाँधकर रखता है।
श्यान बल का सूत्र
किसी तरल की दो समांतर पर्तों के बीच लगने वाला श्यान बल—
जहाँ—
- = श्यान बल
- = पर्तों का संपर्क क्षेत्रफल
- = वेग प्रवणता (दूरी के साथ वेग में परिवर्तन की दर)
- = श्यानता गुणांक (Coefficient of Viscosity)
ऋणात्मक चिन्ह का अर्थ: सूत्र में उपस्थित ऋण (-) चिन्ह यह दर्शाता है कि श्यान बल सदैव द्रव के प्रवाह की दिशा के विपरीत कार्य करता है।
➤ स्टोक का नियम (Sotck’s Law)
स्टोक्स ने सिद्ध किया कि यदि r त्रिज्या की एक छोटी गोलाकार गोली किसी पूर्णतः समांग (Homogeneous) तथा अनन्त विस्तार वाले तरल माध्यम में अंतिम वेग vvv से गति करती है, तो गोली पर तरल द्वारा लगाया गया श्यान बल (Viscous Force)
होता है।
यह श्यान बल सदैव गोली की गति की दिशा के विपरीत कार्य करता है।
जहाँ—
- = गोली पर लगने वाला श्यान बल
- = गोली की त्रिज्या
- = गोली का अंतिम वेग
- = तरल का श्यानता गुणांक
➤ आदर्श द्रव (Ideal Liquid)
वह द्रव जिसके लिए संपीड्यता (Compressibility) तथा श्यानता (Viscosity) दोनों ही शून्य हों, आदर्श द्रव कहलाता है।
(1) असंपीड्य द्रव: असंपीड्य होने का अर्थ है कि द्रव पर कितना ही दाब क्यों न लगाया जाए, उसके आयतन तथा घनत्व में कोई परिवर्तन नहीं होता।
(2) अश्यान द्रव: अश्यान होने का अर्थ है कि जब द्रव की विभिन्न पर्तों के बीच आपेक्षिक गति होती है, तब पर्तों के बीच कोई स्पर्शरेखीय घर्षण बल (Shearing Friction) कार्य नहीं करता।
➤ धारा रेखीय प्रवाह (Streamline Flow)
जब कोई द्रव इस प्रकार प्रवाहित होता है कि द्रव का कोई भी कण जिस बिंदु से गुजरता है, उसी बिंदु से गुजरने वाला प्रत्येक अगला कण ठीक उसी मार्ग का अनुसरण करता है जिस मार्ग से उससे पहले वाला कण गुजर चुका होता है, तब द्रव के इस प्रकार के प्रवाह को धारारेखीय प्रवाह (Streamline या Laminar Flow) कहते हैं।
द्रव के कण के चलने के जिस निश्चित मार्ग का अनुसरण किया जाता है, उसे धारारेखा (Streamline) कहते हैं।
मुख्य विशेषताएँ (Exam Point)
- प्रवाह सुव्यवस्थित एवं नियमित होता है
- द्रव की विभिन्न पर्तें एक-दूसरे के समानांतर बहती हैं
- धारारेखाएँ कभी एक-दूसरे को नहीं काटतीं
- यह प्रवाह सामान्यतः कम वेग पर पाया जाता है
➤ द्रवों के बहने की अविरलता का सिद्धान्त (Principle of Continuity of Liquids Flowing)
यदि कोई असंपीड्य एवं अश्यान द्रव (आदर्श द्रव) किसी असमान अनुप्रस्थ काट वाली नली में धारारेखीय प्रवाह में बह रहा हो, तो नली के प्रत्येक बिंदु पर द्रव के अनुप्रस्थ काट के क्षेत्रफल और वेग का गुणनफल सदैव समान रहता है।
इसी नियम को अविरलता का सिद्धान्त कहते हैं।
यदि नली के दो विभिन्न बिंदुओं पर
- अनुप्रस्थ काट के क्षेत्रफल =
- द्रव के वेग =
तो,
प्रवाह की दर (Rate of Flow)
द्रव के प्रवाह की दर—
अर्थात् आदर्श द्रव के धारारेखीय प्रवाह में प्रवाह की दर स्थिर रहती है।
निष्कर्ष
- वेग
- चौड़ी नली → वेग कम
- पतली नली → वेग अधिक
➤ क्रांतिक वेग (Critical Velocity)
यदि किसी द्रव के प्रवाह का वेग एक निश्चित मान से कम हो, तो द्रव का प्रवाह धारारेखीय (Streamline या Laminar) प्रवाह होता है। द्रव के इस निश्चित अधिकतम वेग को क्रांतिक वेग (Critical Velocity) कहते हैं।
इस वेग पर द्रव का प्रवाह नियमित होता है, अर्थात् किसी भी निश्चित बिंदु पर द्रव की चाल तथा दिशा समय के साथ अपरिवर्तित रहती है।
विक्षुब्ध प्रवाह (Turbulent Flow)
यदि द्रव का वेग क्रांतिक वेग से अधिक हो जाता है, तो द्रव का प्रवाह अनियमित हो जाता है, जिसे विक्षुब्ध प्रवाह (Turbulent Flow) कहते हैं।
इस प्रवाह में—
- द्रव के कणों का मार्ग टेढ़ा-मेढ़ा (Zig-zag) हो जाता है,
- द्रव में भंवर (Eddies/Whirls) उत्पन्न हो जाते हैं,
- चाल और दिशा लगातार बदलती रहती है।
उदाहरण:
- बरसात के समय नदी-नालों का तीव्र प्रवाह
- तेज वेग से बहता जल
संक्षिप्त निष्कर्ष (Exam Point)
- → धारारेखीय प्रवाह
- → विक्षुब्ध प्रवाह
- = क्रांतिक वेग
क्रांतिक वेग से कम वेग होने पर द्रव के बहने पर उसकी श्यानता महत्वपूर्ण भूमिका निभाती है और क्रांतिक वेग से अधिक होने पर उसका वेग उसके घनत्व (density) पर निर्भर करता है।
➤ वेग प्रवणता (Velocity Gradient)
द्रव की दो समांतर पर्तों के बीच, जो प्रवाह की दिशा के लम्बवत् स्थित हों, एकांक दूरी पर होने वाले वेग परिवर्तन को वेग प्रवणता कहते हैं।
यदि दूरी पर स्थित दो पर्तों के बीच वेग में परिवर्तन हो, तो वेग प्रवणता—
इसे दूरी के साथ वेग में परिवर्तन की दर कहा जाता है।
मात्रक
- SI मात्रक : प्रति सेकंड
➤ बरनौली प्रमेय (Bernaulli’s Theorem)
जब कोई असंपीड्य तथा अश्यान द्रव (या गैस) एक स्थान से दूसरे स्थान तक धारारेखीय प्रवाह में प्रवाहित होता है, तब उसके प्रवाह-पथ के प्रत्येक बिंदु पर प्रति एकांक आयतन द्रव की कुल ऊर्जा—
दाब ऊर्जा, गतिज ऊर्जा तथा स्थितिज ऊर्जा—का योग नियतांक रहता है।
जहाँ—
- = दाब ऊर्जा (प्रति एकांक आयतन)
- = द्रव का घनत्व
- = द्रव का वेग
- = गुरुत्वीय त्वरण
- = संदर्भ तल से ऊँचाई
अर्थ एवं निष्कर्ष
- यह समीकरण दर्शाता है कि प्रवाहित द्रव के लिए ऊर्जा संरक्षण का सिद्धान्त लागू होता है।
- जिस स्थान पर द्रव का वेग कम होता है, वहाँ उसका दाब अधिक होता है।
- जिस स्थान पर द्रव का वेग अधिक होता है, वहाँ उसका दाब कम हो जाता है।
संकीर्ण नली का उदाहरण
यदि द्रव को ऐसी नली में प्रवाहित किया जाए जिसका मध्य भाग संकीर्ण हो, तो—
- संकीर्ण भाग में द्रव का वेग अधिकतम होगा,
- तथा उसी भाग में द्रव का दाब न्यूनतम होगा।
प्रमेय की शर्तें (Exam Point)
- द्रव असंपीड्य हो
- द्रव अश्यान हो
- प्रवाह धारारेखीय हो
- कोई ऊर्जा हानि न हो
➤ बरनौली प्रमेय के अनुप्रयोग (Applications of Bernaulli’s Theorem)
(i) वेन्चुरी मीटर (Venturimeter)- वेन्चुरी मीटर बरनौली के प्रमेय पर आधारित एक यंत्र है, जिसकी सहायता से किसी नली में बहने वाले द्रव की प्रवाह-दर (Rate of Flow) ज्ञात की जाती है।
इसमें एक नली XY होती है, जिसका मध्य भाग संकीर्ण (Throat) होता है। नली के दो बिंदुओं—
- X (चौड़ा भाग)
- Z (संकीर्ण भाग)
पर दो ऊर्ध्वाधर नलियाँ जुड़ी रहती हैं। इस यंत्र को उस नली के साथ जोड़ दिया जाता है जिसमें द्रव की प्रवाह-दर ज्ञात करनी हो।
कार्यविधि
जब नली XY में जल प्रवाहित होता है, तब—
- संकीर्ण भाग Z पर द्रव का वेग अधिक होता है,
- अतः Z पर दाब कम हो जाता है,
- जबकि चौड़े भाग X पर दाब अधिक रहता है।
इन दोनों बिंदुओं के दाबांतर को ऊर्ध्वाधर नलियों में जल-स्तर के अंतर द्वारा मापा जाता है। इसी दाबांतर की सहायता से द्रव की प्रवाह-दर ज्ञात की जाती है।
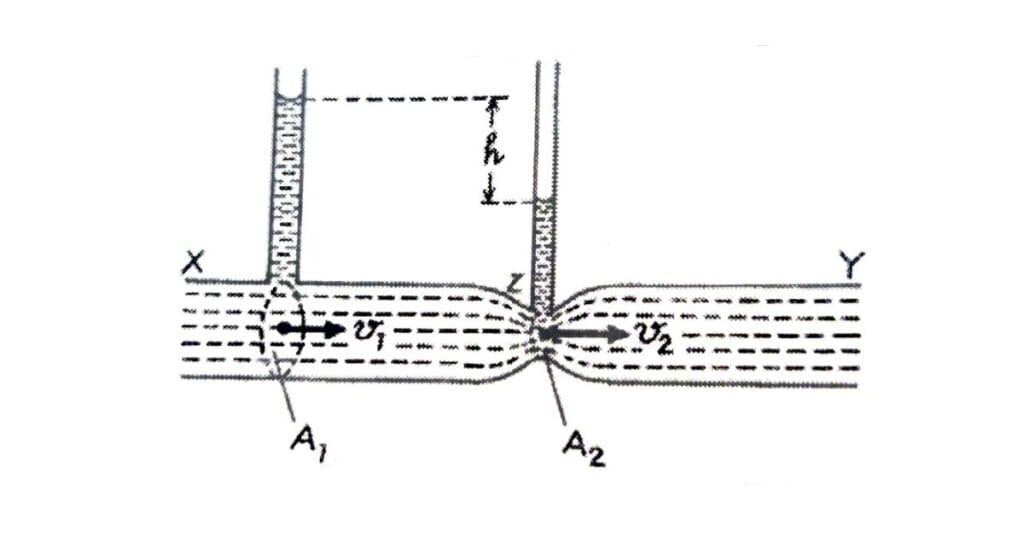
यदि
- = चौड़े भाग का अनुप्रस्थ काट क्षेत्रफल
- = संकीर्ण भाग का अनुप्रस्थ काट क्षेत्रफल
- = दोनों बिंदुओं के बीच दाबांतर (द्रव-स्तर का अंतर)
तो प्रवाह-दर—
(ii) कणित्र (Atomizer)- एटोमाइज़र बरनौली के प्रमेय पर आधारित एक ऐसी युक्ति है, जिसकी सहायता से किसी द्रव की धारा को छोटी-छोटी बूँदों (Spray या फुहारा) के रूप में परिवर्तित किया जाता है।
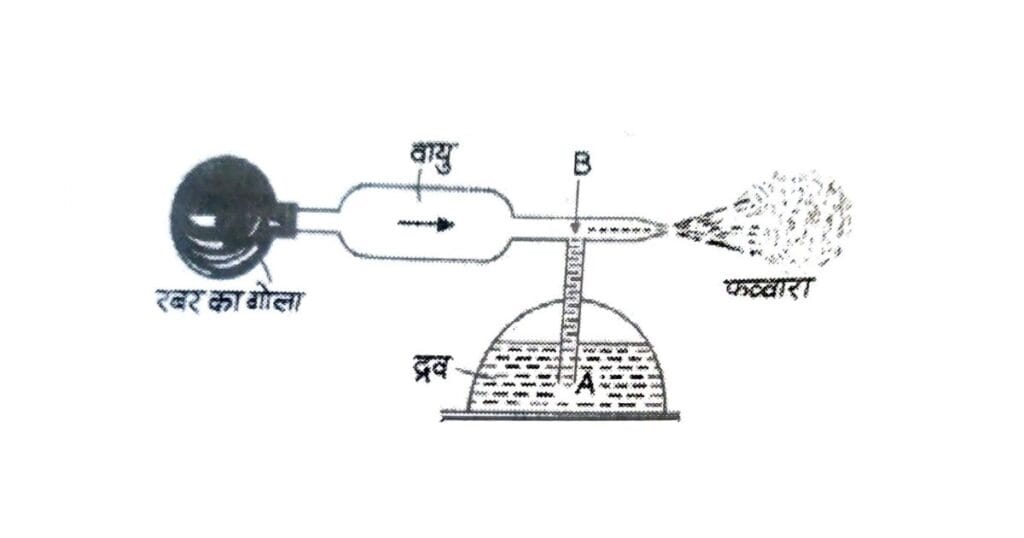
संरचना:
इसमें दो नलियाँ होती हैं—
- एक क्षैतिज नली,
- तथा दूसरी ऊर्ध्वाधर नली,
जो आपस में एक-दूसरे के लम्बवत् जुड़ी होती हैं। ऊर्ध्वाधर नली का निचला सिरा द्रव (जैसे— पानी, इत्र) में डुबोया जाता है।
कार्यविधि:
जब क्षैतिज नली में पीछे की ओर से वायु को अधिक वेग से प्रवाहित किया जाता है, तब—
- क्षैतिज नली के संकीर्ण भाग में वायु का वेग बहुत अधिक हो जाता है,
- परिणामस्वरूप वहाँ दाब कम हो जाता है,
- दाबांतर के कारण द्रव पात्र से ऊर्ध्वाधर नली द्वारा ऊपर चढ़ने लगता है,
- और तेज वेग वाली वायु के साथ मिलकर द्रव फुहारे (Spray) के रूप में बाहर निकलता है।
यह प्रक्रिया बरनौली के प्रमेय के अनुसार होती है, क्योंकि अधिक वेग वाले स्थान पर दाब कम होता है।
उपयोग
- चित्रकारी एवं रंगाई में
- इत्र एवं कीटनाशक छिड़कने में
- चिकित्सकों द्वारा नाक, कान आदि धोने में
निष्कर्ष (Exam Point)
- वेग अधिक → दाब कम
- दाबांतर → द्रव ऊपर उठता है
- एटोमाइज़र → बरनौली प्रमेय का अनुप्रयोग
➤ निर्वात उत्पन्न करने वाला यंत्र (Vaccume Creator)
फिल्टर पम्प का उपयोग किसी पात्र में निर्वात (Partial Vacuum) उत्पन्न करने के लिए किया जाता है।
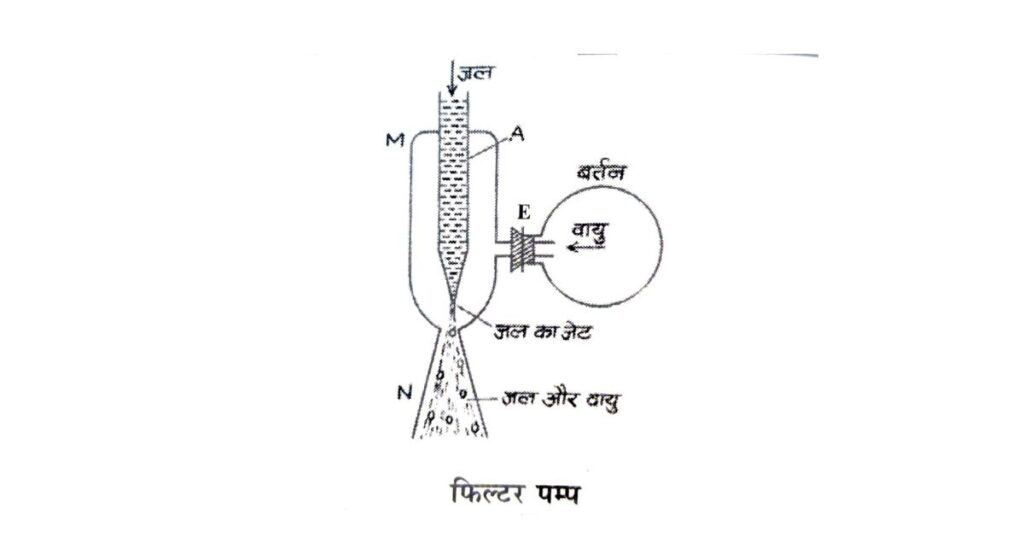
संरचना:
- इसमें एक चौड़ी नली MN होती है।
- इसके ऊपरी भाग में एक अन्य नली A जुड़ी होती है।
- A का ऊपरी सिरा जल की टंकी से जुड़ा होता है।
- A का निचला सिरा बारीक होता है जिससे जल जेट के रूप में बाहर निकलता है।
- जिस पात्र की वायु निकालनी हो, उसे नली MN से जोड़ा जाता है।
कार्यविधि:
- जब नली A के बारीक छेद से जल उच्च वेग से जेट के रूप में बाहर निकलता है,
- जल जेट के समीप वायु का दाब कम हो जाता है।
- इस दाबांतर के कारण पात्र की वायु नली MN के माध्यम से जेट के पास प्रवेश करने लगती है।
- इस प्रक्रिया से पात्र में आंशिक निर्वात (Partial Vacuum) उत्पन्न हो जाता है।
सिद्धान्त
- यह कार्य बरनौली प्रमेय पर आधारित है।
- उच्च वेग वाले जेट के पास दाब घटने के कारण निचले दाब की जगह हवा/वायु खिंचती है।
प्रयोग (Applications)
- लैब में वैक्यूम बनाने के लिए
- तरल को संस्रावित (Suction) करने में
➤ टारसौली का प्रमेय (Tarsauli’s Theorem)
यदि कोई वस्तु h ऊँचाई से स्वतंत्रतापूर्वक गिरती है, तो गति के तृतीय समीकरण—
के अनुसार उसका वेग,
होता है।
यदि किसी द्रव को स्वतंत्रतापूर्वक छोड़ा जाए (अर्थात् उसका प्रारम्भिक वेग शून्य हो), तो ऊँचाई से गिरने पर द्रव का वेग भी होगा।
निष्कर्ष (टॉरिसेली का प्रमेय)
किसी पात्र की दीवार में बने छोटे छिद्र से निकलने वाले द्रव का वेग (बहिःस्राव वेग) उसी वेग के बराबर होता है, जो द्रव अपने मुक्त पृष्ठ से छिद्र तक स्वतंत्रतापूर्वक गिरने पर प्राप्त करता है।
अतः,
जहाँ—
- = द्रव का बहिःस्राव वेग
- = द्रव के मुक्त पृष्ठ और छिद्र के बीच की ऊँचाई
- = गुरुत्वीय त्वरण
शर्तें (Exam Point)
- द्रव असंपीड्य हो
- द्रव अश्यान हो
- छिद्र छोटा हो
- पात्र खुला हो (वायुदाब समान)
अर्थ: यह प्रमेय दर्शाता है कि द्रव के बहाव में स्थितिज ऊर्जा का गतिज ऊर्जा में रूपांतरण होता है, अर्थात् यह भी ऊर्जा संरक्षण सिद्धान्त पर आधारित है।
यह भी पढ़ें : द्रव स्थैतिकी (Hydrostatics)

1 thought on “पृष्ठ तनाव (Surface Tension)”