गैसों का अणु गति सिद्धान्त (Kinetic Theory of Gases)

इस लेख में हम गैसों का अणु गति सिद्धान्त के बारे में जानकारी प्राप्त करेंगे । इसमें दी गई जानकारी आपके लिए सहायक सिद्ध होगी तो आइए इसे अपनी पूरी अंतः शक्ति से पढ़ते हैं।

➤ आदर्श गैस (Ideal Gas)

आदर्श गैस एक ऐसी काल्पनिक गैस है जिसके गुण अत्यंत निम्न दाब एवं उच्च ताप पर वास्तविक गैसों के गुणों के समान होते हैं। आदर्श गैस में निम्नलिखित गुणों की कल्पना की जाती है—

1. आदर्श गैस ताप तथा दाब की सभी अवस्थाओं में बॉयल का नियम, चार्ल्स का नियम एवं दाब का नियम पूर्णतः पालन करती है।
2. आदर्श गैस का आयतन प्रसार गुणांक (Coefficient of Volume Expansion) तथा दाब प्रसार गुणांक (Coefficient of Pressure Expansion) आपस में बराबर होते हैं।
3. आदर्श गैस के अणुओं के बीच कोई आकर्षण या प्रतिकर्षण बल नहीं होता है।
4. आदर्श गैस के अणुओं का आकार अत्यंत सूक्ष्म (Infinitesimally Small) माना जाता है, अतः गैस के कुल आयतन की तुलना में अणुओं का आयतन नगण्य होता है।

वास्तविक गैसों में ऑक्सीजन, नाइट्रोजन, हाइड्रोजन एवं हीलियम को आदर्श गैस की परिकल्पना के काफी निकट माना जाता है।

➤ आदर्श गैस का गत्यात्मक सिद्धान्त (Mobility Theory of Ideal Gasses)

आदर्श गैस के गतिज सिद्धांत के उपपादन

1. गैस के सभी अणु एक जैसे, दृढ़ (Rigid) तथा अत्यंत सूक्ष्म गोलाकार कण होते हैं।
2. गैस के अणु निरंतर अनियमित गति करते रहते हैं। यद्यपि अणु गतिशील रहते हैं, फिर भी किसी निश्चित आयतन में अणुओं की औसत संख्या स्थिर रहती है।
3. गैस के अणुओं के बीच कोई आकर्षण अथवा प्रतिकर्षण बल कार्य नहीं करता। जब दो अणु आपस में टकराते हैं, तो उनकी दिशा एवं वेग बदल जाते हैं, जिससे उनकी गति अनियमित बनी रहती है।
4. अणुओं की आपसी टक्कर तथा पात्र की दीवारों से टक्कर पूर्णतः प्रत्यास्थ (Perfectly Elastic) होती है। अतः सामान्य ताप एवं दाब पर गैस की माध्य गतिज ऊर्जा में कोई ह्रास नहीं होता।
5. गैस के अणुओं की गति पर गुरुत्वाकर्षण बल का प्रभाव नगण्य होता है, क्योंकि अणुओं का द्रव्यमान बहुत कम तथा वेग अत्यधिक होता है।

आदर्श गैस का दाब (महत्वपूर्ण निष्कर्ष)

“आदर्श गैस का दाब, उसके प्रति एकांक आयतन की कुल गतिज ऊर्जा का दो-तिहाई होता है।”

गणितीय रूप में—$$P = \frac{2}{3}\, (\text{प्रति इकाई आयतन की गतिज ऊर्जा})$$

या$$P = \frac{1}{3}\, \rho \bar{c}^2$$

जहाँ—

• $P$ = गैस का दाब
• $\rho$ = गैस का घनत्व
• $\bar{c}$ = अणुओं का माध्य वेग

➤ बॉयल का नियम (Boyal’s Law)

यदि किसी निश्चित मात्रा की गैस का ताप स्थिर रखा जाए, तो गैस के अणुओं का वेग-वर्ग माध्य भी स्थिर रहता है। इस अवस्था में गैस का दाब (P) उसके आयतन (V) के व्युत्क्रमानुपाती होता है।

अर्थात्—$$P \propto \frac{1}{V}$$

या$$PV = \text{नियतांक}$$

जहाँ—

• $P$ = गैस का दाब
• $V$ = गैस का आयतन

यह नियम केवल आदर्श गैस के लिए पूर्णतः सत्य होता है।

Note:

1. यदि गैस के ताप को नियत रखते हुए उसका दाब दोगुना कर दिया जाए, तो उसका आयतन आधा हो जाता है।
2. यदि गैस का दाब आधा कर दिया जाए, तो उसका आयतन दोगुना हो जाता है।

➤ चार्ल्स का नियम (Charl’s Law)

गैस के दिए गए द्रव्यमान के लिए यदि गैस का दाब स्थिर रखा जाए, तो गैस का आयतन (V) उसके परम ताप (T) के अनुक्रमानुपाती होता है।

अर्थात्—$$V \propto T \quad (जब\; P = \text{नियत})$$

या$$\frac{V}{T} = \text{नियतांक}$$

जहाँ—

• $V$ = गैस का आयतन
• $T$ = गैस का परम ताप (केल्विन में)

Note:

• ताप बढ़ाने पर गैस का आयतन बढ़ता है।
• ताप घटाने पर गैस का आयतन घटता है।

यह नियम भी आदर्श गैस के लिए पूर्णतः सत्य होता है।

➤ क्रान्तिक ताप (Critical Temperature)

प्रत्येक गैस के लिए एक निश्चित ताप होता है, जिसके नीचे गैस को केवल दाब बढ़ाकर द्रवित किया जा सकता है।
परंतु यदि गैस का ताप इस निश्चित ताप से अधिक हो, तो उसे कितना भी अधिक दाब देने पर भी द्रवित नहीं किया जा सकता।

इस निश्चित ताप को उस गैस का क्रान्तिक ताप कहते हैं।

उदाहरण

• कार्बन डाइऑक्साइड (CO₂) का क्रान्तिक ताप = 31.1 °C
• ऑक्सीजन (O₂) का क्रान्तिक ताप = –118 °C

अतः 0 °C ताप पर—

• CO₂ का ताप उसके क्रान्तिक ताप से कम है, इसलिए CO₂ को केवल दाब डालकर द्रवित किया जा सकता है।
• जबकि O₂ का ताप उसके क्रान्तिक ताप से अधिक है, इसलिए O₂ को केवल दाब डालकर द्रवित नहीं किया जा सकता।

➤ क्रान्तिक दाब (Critical Pressure)

क्रान्तिक ताप पर किसी गैस को द्रवित करने के लिए आवश्यक न्यूनतम दाब को उस गैस का क्रान्तिक दाब कहते हैं।

महत्वपूर्ण बिंदु

• क्रान्तिक दाब केवल क्रान्तिक ताप पर परिभाषित किया जाता है।
• यदि गैस का ताप क्रान्तिक ताप से अधिक हो, तो कितना भी अधिक दाब देने पर गैस द्रवित नहीं होगी।
• गैस के द्रवीकरण में क्रान्तिक ताप एवं क्रान्तिक दाब दोनों का विशेष महत्व होता है।

➤ क्रान्तिक आयतन (Critical Volume)

क्रान्तिक ताप एवं क्रान्तिक दाब पर एकांक द्रव्यमान की गैस का जो आयतन होता है, उसे उस गैस का क्रान्तिक आयतन कहते हैं।

महत्वपूर्ण बिंदु

• क्रान्तिक आयतन, गैस के क्रान्तिक स्थिरांकों (क्रान्तिक ताप, क्रान्तिक दाब एवं क्रान्तिक आयतन) में से एक है।
• यह गैस के द्रवीकरण के अध्ययन में महत्वपूर्ण भूमिका निभाता है।
• प्रत्येक गैस के लिए क्रान्तिक आयतन का मान भिन्न-भिन्न होता है।

➤ वाष्प तथा गैस (Vapour and Gas)

वाष्प (Vapour)

वे पदार्थ जो सामान्य ताप एवं दाब पर ठोस या द्रव अवस्था में होते हैं, किंतु जब वे गैसीय अवस्था में आ जाते हैं तो उन्हें वाष्प कहा जाता है।
उदाहरण— जल की वाष्प, कपूर की वाष्प आदि।

गैस (Gas)

वे पदार्थ जो सामान्य ताप एवं दाब पर स्वाभाविक रूप से गैसीय अवस्था में रहते हैं, उन्हें गैस कहते हैं।
उदाहरण— हाइड्रोजन (H₂), ऑक्सीजन (O₂), नाइट्रोजन (N₂) आदि।

द्रवीकरण की दृष्टि से अंतर

• वाष्प को केवल दाब बढ़ाकर ही द्रवित किया जा सकता है।
• गैस को द्रवित करने के लिए पहले उसे उसके क्रान्तिक ताप तक ठंडा करना आवश्यक होता है, इसके बाद दाब डालकर उसे द्रवित किया जा सकता है।

➤ वाण्डरवाल समीकरण (Wanderwal’s Equation)

वाण्डरवाल का समीकरण गैसों की अवस्था का एक महत्वपूर्ण समीकरण है, जिसे वाण्डरवाल ने सन् 1877 में प्रस्तुत किया था। यह समीकरण वास्तविक गैसों के व्यवहार का काफी सीमा तक सही वर्णन करता है।

आदर्श गैसों के लिए अवस्था समीकरण—$$PV = nRT$$

पूर्णतः सत्य होता है, परन्तु वास्तविक गैसें इस समीकरण का ठीक प्रकार पालन नहीं करतीं।

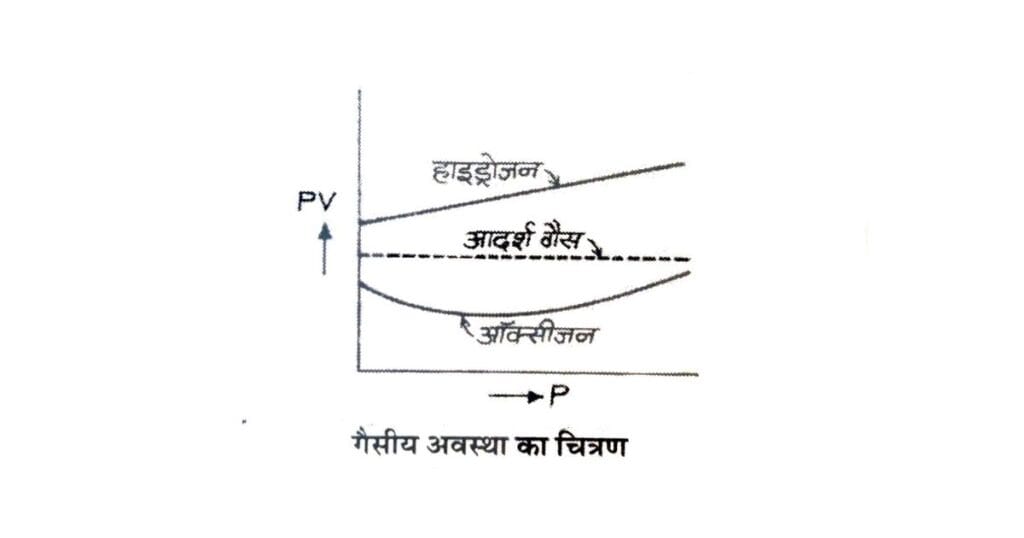
वास्तविक गैसों का व्यवहार

आदर्श गैस के लिए ताप नियत रहने पर $PV$ का मान नियत रहता है,
किन्तु वास्तविक गैसों में दाब बढ़ाने पर PV का मान बदलता रहता है, अर्थात् यह नियत नहीं रहता।

• हाइड्रोजन (H₂) के लिए दाब बढ़ाने पर $PV$ का मान लगातार बढ़ता है।
• ऑक्सीजन (O₂) जैसी गैसों में दाब बढ़ाने पर पहले $PV$ का मान घटता है,
  और अधिक दाब पर पुनः बढ़ने लगता है।

इससे स्पष्ट होता है कि विभिन्न वास्तविक गैसों का व्यवहार दाब परिवर्तन के साथ भिन्न-भिन्न होता है।

वाण्डरवाल समीकरण

वास्तविक गैसों के इस विचलन को समझाने के लिए वाण्डरवाल ने अणुओं के

• सीमित आयतन, तथा
• अंतराअणुक आकर्षण बल

को ध्यान में रखते हुए अपना समीकरण प्रस्तुत किया—$$\left(P + \frac{a n^2}{V^2}\right)(V – nb) = nRT$$

जहाँ—

• $a$ = अंतराअणुक आकर्षण बल से संबंधित स्थिरांक
• $b$ = अणुओं के वास्तविक आयतन से संबंधित स्थिरांक
• $R$ = सार्वत्रिक गैस नियतांक
• $T$ = गैस का परम ताप
• $P$ = दाब
• $V$ = आयतन

द्रवों तथा ठोसों का अणुगति मॉडल (Kinetic Model of Liquids and Solids)

➤ अन्तराण्विक बल (Inter Molecular Force)

प्रत्येक पदार्थ अणुओं (Molecules) से मिलकर बना होता है। प्रत्येक अणु में एक धनावेशित नाभिक तथा उसके चारों ओर ऋणावेशित इलेक्ट्रॉन होते हैं। किसी अणु के नाभिक का कुल धनावेश, उसके इलेक्ट्रॉनों के कुल ऋणावेश के बराबर होता है।
इस कारण अणु वैद्युत उदासीन होते हैं।

फिर भी, जब अणु एक-दूसरे के निकट आते हैं, तो उनमें आवेशों का वितरण इस प्रकार हो जाता है कि विपरीत आवेशों के बीच का आकर्षण बल, समान आवेशों के बीच के प्रतिकर्षण बल से अधिक हो जाता है।

परिणामस्वरूप अणुओं के बीच एक शुद्ध (नेट) आकर्षण बल कार्य करता है।
अणुओं के बीच कार्य करने वाले इसी आकर्षण बल को अंतराण्विक बल (Intermolecular Force) कहा जाता है।

महत्व

• अंतराण्विक बल पदार्थ की ठोस, द्रव एवं गैसीय अवस्थाओं के लिए उत्तरदायी होता है।
• इसी बल के कारण गैसों का द्रवीकरण, द्रवों में पृष्ठ तनाव, तथा ठोसों में दृढ़ता पाई जाती है।

➤ साम्य दूरी (Equilibrium Distance)

अंतराण्विक बल एवं अणुओं के बीच दूरी का संबंध

जब पदार्थ के अणुओं के बीच की दूरी घटती जाती है, तो उनके बीच कार्य करने वाले नेट आकर्षण बल का मान बढ़ता जाता है।
परन्तु जब अणु अत्यधिक पास आ जाते हैं, तब उनके आवेशों का वितरण बदलने लगता है, जिसके परिणामस्वरूप—

• आकर्षण बल का मान घटने लगता है, तथा
• प्रतिकर्षण बल का मान बढ़ने लगता है।

अत्यधिक निकट दूरी पर ऐसी स्थिति आ सकती है जब नेट आकर्षण बल के स्थान पर नेट प्रतिकर्षण बल कार्य करने लगे।

साम्य दूरी (Equilibrium Distance)

इन दोनों अवस्थाओं (आकर्षण एवं प्रतिकर्षण) के बीच एक ऐसी स्थिति होती है, जिसमें आकर्षण बल एवं प्रतिकर्षण बल का मान बराबर हो जाता है,
अतः अणुओं के बीच कार्य करने वाला नेट बल शून्य होता है।

इस स्थिति में अणुओं के बीच की दूरी को साम्य दूरी (r_0​) कहते हैं।

• साम्य दूरी का परिमाण लगभग $$r_0 \approx 10^{-10}\ \text{m}$$

महत्वपूर्ण निष्कर्ष

• यदि अणुओं के बीच की दूरी $r > r_0$​ हो, तो वे एक-दूसरे को आकर्षित करते हैं।
• यदि दूरी $r < r_0$​ हो, तो वे एक-दूसरे को प्रतिकर्षित करते हैं।

👉 यही सिद्धांत पदार्थ की संरचना, स्थायित्व तथा विभिन्न अवस्थाओं को समझने का आधार है।

➤ द्रवों का आण्विक मॉडल (Molecular Model of Liquid’s)

द्रव अवस्था में अणुओं के गुण

1. द्रवों में प्रत्येक अणु अनेक समीपवर्ती अणुओं के बल-क्षेत्र में रहता है, परन्तु अणुओं में पर्याप्त गतिज ऊर्जा होने के कारण वे द्रव की परिसीमा (Boundaries) के भीतर स्वतंत्र रूप से गति करते रहते हैं।
2. द्रव अवस्था में अणुओं का स्थान (Position) तथा क्रम (Order) नियत नहीं होता।
3. द्रवों में अणुओं के बीच की औसत साम्य दूरी (r₀​) लगभग

$$10^{-10}\ \text{m}$$

की कोटि की होती है।

4. द्रवों के अणु मुख्यतः अपने निकटवर्ती अणुओं से ही टकराते हैं, फिर भी उनकी स्थिति में निरंतर विस्थापन होता रहता है।

द्रवों का वाष्पन एवं क्वथन (Vaporisation and Boiling)

वाष्पीकरण (Vaporisation)

द्रव के अणु निरंतर अनियमित गति करते रहते हैं तथा आपस में टकराकर ऊर्जा का आदान-प्रदान करते रहते हैं। इस कारण कुछ अणुओं की गतिज ऊर्जा अधिक तथा कुछ की कम हो जाती है।

जब अधिक गतिज ऊर्जा वाला कोई अणु द्रव के पृष्ठ तक पहुँचता है, तो वह द्रव के भीतर स्थित अणुओं के आकर्षण बल के बावजूद द्रव को छोड़कर वायुमंडल में चला जाता है।
इस प्रक्रिया को वाष्पीकरण कहते हैं।

वाष्पीकरण से शीतलन

चूँकि वाष्पीकरण में केवल अधिक गतिज ऊर्जा वाले अणु ही द्रव से बाहर निकलते हैं, इसलिए द्रव में शेष अणुओं की औसत गतिज ऊर्जा कम हो जाती है।
फलस्वरूप द्रव का ताप घटता जाता है, अर्थात् वाष्पीकरण से द्रव ठंडा हो जाता है।

ताप का प्रभाव एवं क्वथनांक

जब द्रव को बाहर से ऊष्मा दी जाती है, तो द्रव के अणुओं की गतिज ऊर्जा बढ़ती है, जिससे—

• द्रव का ताप बढ़ता है
• द्रव के पृष्ठ से अधिक अणु बाहर निकलते हैं
• अर्थात् वाष्पीकरण की दर बढ़ जाती है

द्रव को निरंतर गर्म करने पर एक विशेष ताप आता है, जिस पर द्रव के सभी अणु अंतराण्विक बलों के बंधन से मुक्त होकर द्रव से बाहर जाने लगते हैं।
इस ताप को द्रव का क्वथनांक (Boiling Point) कहते हैं।

वाष्पन की गुप्त ऊष्मा (Latent Heat of Vaporization)

क्वथनांक पर द्रव को और ऊष्मा देने पर द्रव का ताप नहीं बढ़ता, क्योंकि दी गई ऊष्मा—

• अणुओं की गतिज ऊर्जा बढ़ाने के बजाय
• अणुओं को उनके पारस्परिक आकर्षण बलों के विरुद्ध दूर-दूर करने (अर्थात् स्थितिज ऊर्जा बढ़ाने) में खर्च होती है।

क्वथनांक पर द्रव को गैस में परिवर्तित करने के लिए आवश्यक इसी ऊष्मा को वाष्पन की गुप्त ऊष्मा कहते हैं।

➤ ठोसों का आण्विक मॉडल (Molecular Model of Solids)

ठोस अवस्था में अणुओं के गुण

1. ठोसों में अणु नियमित क्रम (Regular Order) में सजे रहते हैं।
   अतः प्रत्येक अणु का स्थान या स्थिति निश्चित होती है।
2. ठोस में दो अणुओं के मध्य की दूरी की कोटि (Order) द्रवों में अणुओं के मध्य दूरी के समान होती है, जो लगभग

$$10^{-10}\ \text{m}$$

की कोटि की होती है।

3. ठोस अवस्था में अणु अपनी साम्य स्थिति (Equilibrium Position) के दोनों ओर केवल कम्पन (Vibration) करते हैं,
   परन्तु अपनी स्थिति को स्थायी रूप से नहीं छोड़ते।
4. ठोस के अणुओं की गतिज ऊर्जा, द्रव के अणुओं की गतिज ऊर्जा की तुलना में कम होती है।

ठोसों का गलन (Meltting of Solids)

जब किसी ठोस को गरम किया जाता है, तो उसके अणुओं की ऊर्जा बढ़ती है और वे अधिक आयाम से कम्पन करने लगते हैं।

गर्म करने पर एक विशेष स्थिति आती है, जब अणुओं का कम्पन इतना बढ़ जाता है कि वे अपनी साम्य स्थितियाँ छोड़ने लगते हैं और उनका क्रम अनियमित हो जाता है।
इस अवस्था में अणु ठोस में इधर-उधर घूमने-फिरने लगते हैं।
इसे ठोस का गलना (Melting) कहते हैं।

गलनांक (Melting Point)

ठोस गलते समय उसका ताप स्थिर रहता है। क्योंकि इस समय ठोस को दी जाने वाली ऊष्मा:

• अणुओं की गतिज ऊर्जा नहीं बढ़ाती,
• बल्कि अणुओं के मध्य आकर्षण बलों के विरुद्ध दूरी बढ़ाने (स्थितिज ऊर्जा बढ़ाने) में खर्च होती है।

इस स्थिर ताप को ठोस का गलनांक (Melting Point) कहते हैं।

गुप्त ऊष्मा (Latent Heat of Fusion)

गलते समय दी गई ऊष्मा केवल अणुओं को आकर्षण बलों से मुक्त करने में व्यय होती है, और इसे ठोस की गुप्त ऊष्मा (Latent Heat of Melting / Fusion) कहा जाता है।$$\text{Latent Heat of Fusion} = \text{ऊष्मा जो अणुओं की स्थितिज ऊर्जा बढ़ाने में लगती है}$$

महत्वपूर्ण बिंदु

• गलते समय ठोस का ताप स्थिर रहता है।
• ऊष्मा केवल अणुओं के आकर्षण बलों को तोड़ने में खर्च होती है।
• अणु क्रमशः द्रव में स्वतंत्र रूप से गतिशील हो जाते हैं।

यह भी पढ़ें : प्रत्यास्थता (Elasticity