संख्या पद्धति ( Number System)

1. कम्प्यूटर में प्रयुक्त होने वाली संख्या पद्धति : मनुष्य गणना के लिए दशमलव आधारी संख्या पद्धति (Decimal number system) का प्रयोग करता है जिसमें 0 से 9 तक (कुल 10) अंकों का प्रयोग किया जाता है। अन्य सभी अंक इन्हीं अंकों से मिलकर बनते हैं। परन्तु कम्प्यूटर दशमलव आधारी संख्या पद्धति का प्रयोग नहीं करता है। कम्प्यूटर में प्रयोग होने वाली संख्या पद्धतियां हैं—

(a) द्विआधारी संख्या पद्धति (Binary number system)

(b) आक्टल संख्या पद्धति (Octal number system)

(c) हैक्साडेसिमल संख्या पद्धति (Hexadecimal number system)

2. द्विआधारी संख्या पद्धति (Binary number System) : कम्प्यूटर एक इलेक्ट्रानिक मशीन है जो विद्युत धारा पर कार्य करता है। यह केवल दो ही परिस्थितियों को जान सकता है। पहला, जब परिपथ में धारा प्रवाहित हो रही है अर्थात परिपथ का स्विच ऑन (ON) है तो इसे संकेत ‘1’ कहा जाता है। दूसरी स्थिति में परिपथ में धारा प्रवाहित नहीं हो रही है, अर्थात् परिपथ का स्विच ऑफ (OFF) है तो इसे संकेत ‘0’ कहा जाता है। इससे हम कह सकते हैं कि कम्प्यूटर केवल द्विआधारी संख्या पद्धति की पहचान कर सकता है। इसी कारण कम्प्यूटर को डाटा या निर्देश देने से पहले उसे 0 या 1 (ऑफ या ऑन) में बदलना पड़ता है।

बाइनरी संख्या पद्धति में इन दो अंकों 0 और 1 को बाइनरी डिजिट (Binary Digit) या संक्षेप में बिट (Bit) कहते हैं। संख्या पद्धति में किसी भी संख्या का मान उसके स्थानीय मान पर निर्भर करता है।

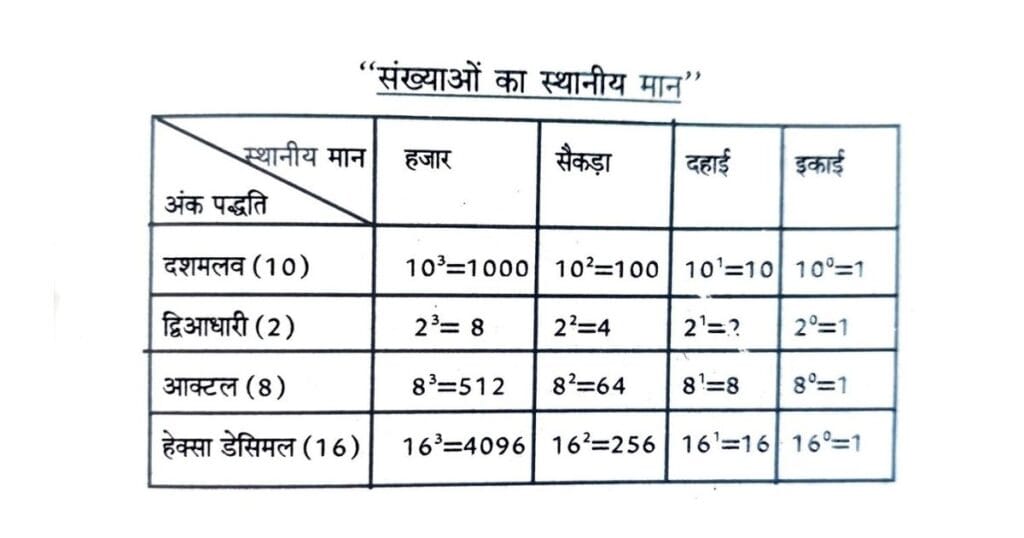
दशमलव पद्धति में आधार 10 होता है तथा इकाई के अंक का स्थानीय मान 10⁰ = 1 होता है, दहाई के अंक का स्थानीय मान 10¹ = 10 तथा सैकड़ा के अंक का स्थानीय मान 10² = 100 होता है। किसी अंक का कुल मान उस अंक तथा उसके स्थानीय मान के गुणनफल के बराबर होता है।

जैसे : 587₍₁₀₎ में 7 का स्थानीय मान = 7 * 10⁰ = 7

578₍₁₀₎ में 7 का स्थानीय मान = 7 * 10¹ = 70

758₍₁₀₎ में 7 का स्थानीय मान = 7 * 10² = 700

इसी प्रकार द्विआधारी संख्या पद्धति में आधार 2 होता है। इकाई के अंक का स्थानीय मान 2⁰ = 1 होता है, दहाई के अंक का स्थानीय मान 2¹ = 2 तथा सैकड़ा के अंक का स्थानीय मान 2² = 4 होता है।

इसी स्थानीय मान के आधार पर एक संख्या पद्धति के अंकों का परिवर्तन दूसरी संख्या पद्धति में किया जाता है।

2.1. दशमलव का द्विआधारी में परिवर्तन (Conversion from Decimal to Binary)

दशमलव को द्विआधारी में बदलने के लिए दशमलव संख्या को 2 से भाग देते हैं। भागफल को नीचे लिखकर शेष को अलग लिखते हैं जो द्विआधारी संख्या का सबसे दाया अंक (LSD- Least Significant Digit) होता है। पुनः भागफल में 2 से भाग देते हैं और यह प्रक्रिया तब तक दुहरायी जाती है जब तक भागफल 0 न रह जाय। अंतिम शेष द्विआधारी संख्या का सबसे बायां अंक (MSD-Most Significant Digit) होता है। प्रत्येक स्थिति में लिखी गई शेष संख्या नीचे (MSD) से ऊपर (LSD) की ओर द्विआधारी संख्या को निरूपति करता है।

उदाहरण : 25₍₁₀₎ को द्विआधारी में बदलें
हल :

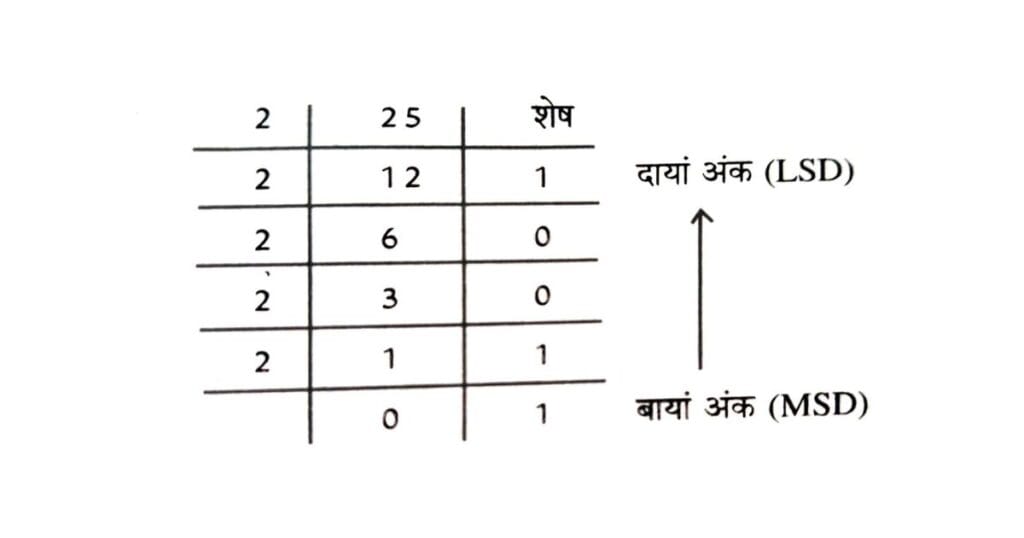
25₍₁₀₎ = 11001₍₂₎

दशमलव अंकों के बाइनरी तुल्यांक

2.2 द्विआधारी का दशमलव में परिवर्तन (Conversion from Binary to Decimal)

द्विआधारी अंकों को दशमलव में परिवर्तित करने के लिए उसके अंकों के मान को स्थानीय मान से गुणा कर उन्हें जोड़ दिया जाता है।

उदाहरण : 10101₍₂₎ को दशमलव में बदलें।

हल : संख्या  1 0 1 0 1
स्थानीय मान 2⁴ 2³ 2² 2¹ 2⁰

10101₍₂₎ = (1 * 2⁴) + (0 * 2³) + (1 * 2²) (0 * 2¹) + (1 * 2⁰)
= (1 * 16) + (0 * 8) + (1 * 4) (0 * 2) + (1 * 1)
= 16 + 0 + 4 + 0 + 1
=21₍₁₀₎

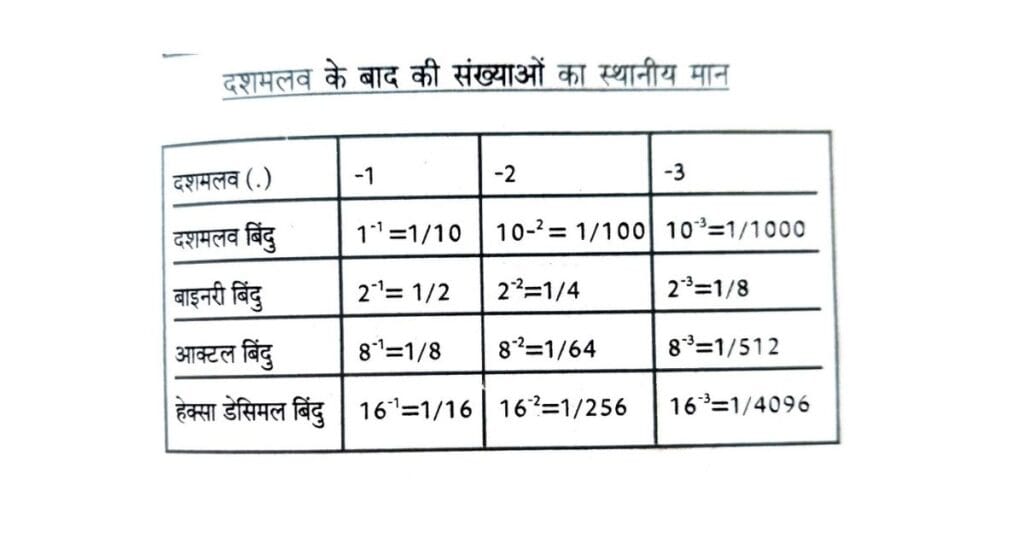
2.3 दशमलव भिन्न का बाइनरी में परिवर्तन (Conversion of Decimal Fraction to Binary Fraction)

दशमलव भिन्न को 2 से गुणा करते हैं। गुणनफल में पूर्ण संख्या को अलग लिखते हैं जो बाइनरी भिन्न का बाया अंक (MSD) होता है। भिन्न को पुनः 2 से गुणा करते हैं और यह तब तक दोहराते हैं जब तक भिन्न शून्य न हो जाय या बाइनरी भिन्न के आवश्यक अंक पूरे न हो जाए।

2.4 बाइनरी भिन्न का दशमलव भिन्न में परिवर्तन (Conversion of Binary Fraction to Decimal Fraction)

बाइनरी बिंदु के बाद के अंकों को उनके स्थानीय मान से गुणा कर जोड़ देते हैं।

उदाहरण : 0.101₍₂₎ को दशमलव में बदलें

हल : 101₍₂₎ = (1*2^-1 ) + (0*2^-2) + (1*2^-3)
= (1 * 0.5) + (0 * 0.25) + (1 * 0.125)
= .5 + 0 + .125
=.625₍₁₀₎

3. आक्टल संख्या पद्धति (Octal number system):

इसमें आधार 8 होता है तथा 0,1, 2,3, 4, 5, 6 और 7 (कुल 8) संख्याओं का प्रयोग किया जाता है।

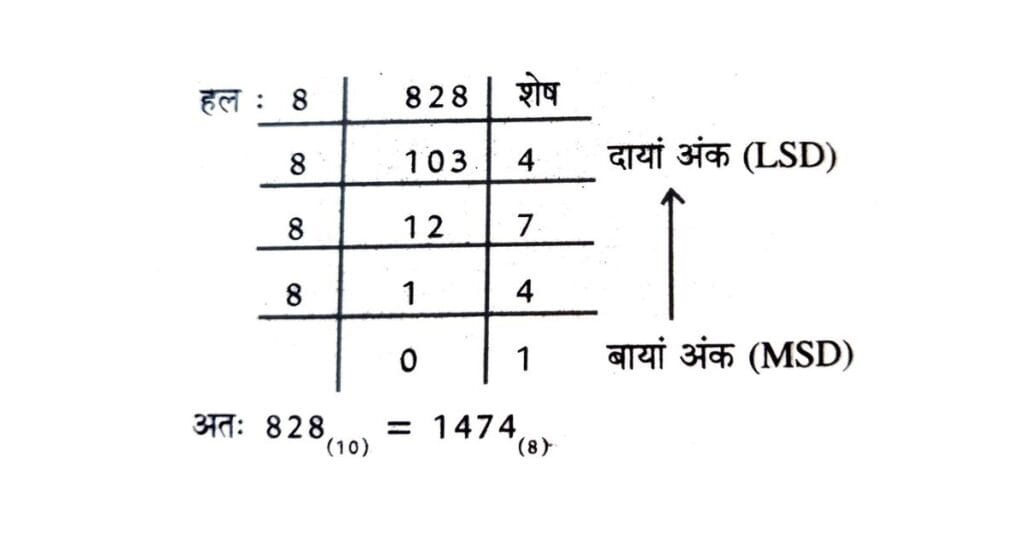
3.1 दशमलव का आक्टल में परिवर्तन (Conversion from Decimal to Octal)

इसमें भाग शेष विधि का प्रयोग किया जाता है।

उदाहरण : 828₍₁₀₎ को आक्टल में बदले

3.2 आक्टल का दशमलव में परिवर्तन (Conversion from Octal to Decimal)

अंकों को उनके स्थानीय मान से गुणा कर जोड़ देते हैं।.

उदाहरण : 1672₍₈₎ को दशमलव में बदलें
हल : 1672₍₈₎ = (1 * 8³) + (6 * 8²) + (7 * 8¹) + (2 * 8⁰)
= (1 * 512) + (6 * 64) + (7 * 8) + (2 * 1)
= 512 + 384 + 56 + 2
= 954₍₁₀₎ 

3.3 आक्टल का बाइनरी में परिवर्तन (Conversion from Octal to Binary)

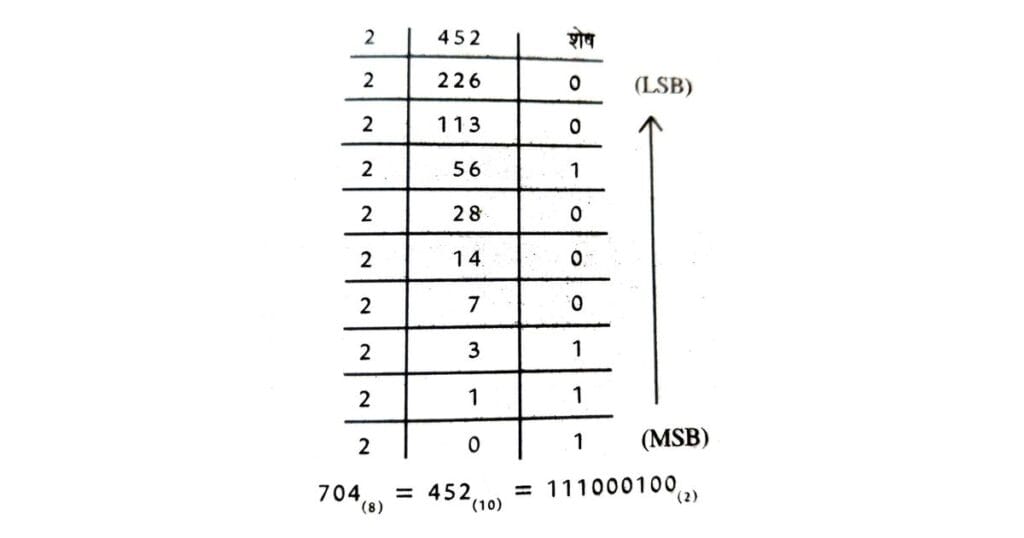
उदाहरण : 704₍₈₎ को बाइनरी में बदलें।

हल : प्रथम विधि : आक्टल संख्या को दशमलव में बदलते हैं और फिर दशमलव को बाइनरी में बदलते हैं।

704 ₍₈₎= (7×8²) + (0x8¹) + (4×8⁰)
=7×64 + 0 + 4×1

= 448 + 4 = 452⁽¹⁰⁾

दूसरी विधि (संक्षिप्त विधि) : आक्टल संख्याओं को उनके तीन अक्षरों के बाइनरी अंक समूह तुल्यांक से प्रतिस्थापित कर देते हैं।

3.4. बाइनरी का आक्टल में परिवर्तन (Conversion from Binary to Octal)

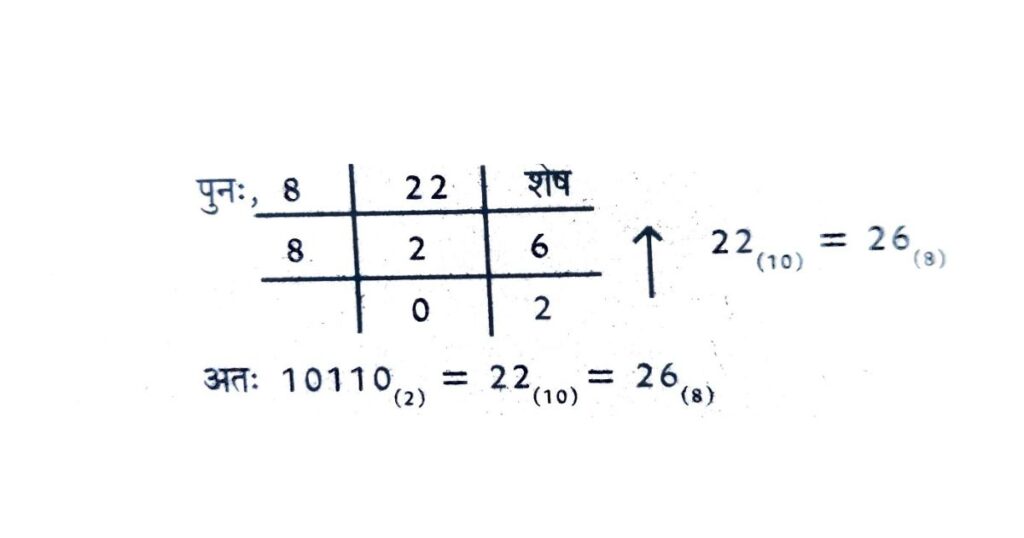
उदाहरण : 10110₍₂₎ को आक्टल में बदलें।

हल : प्रथम विधि : बाइनरी को दशमलव में बदलें और फिर दशमलव को आक्टल में बदलें।

10110₍₂₎ = (1 * 2⁴) + (0 * 2³) + (1 * 2²) + (1 * 2¹) + (0 * 2⁰)
= 16 + 0 + 4 + 2 + 0
=22₍₁₀₎

दूसरी विधि (संक्षिप्त विधि) : दायें से शुरू कर तीन बाइनरी अंकों का समूह बना लेते हैं तथा उनका आक्टल तुल्यांक प्रतिस्थापित कर देते हैं। सबसे बायीं ओर के समूह को तीन अंकों का बनाने के लिए बायीं ओर शून्य जोड़ देते हैं।

10 110₍₂₎ = 10, 110 ₍₂₎
                  = 2 6 =26₍₈₎

4. हेक्साडेसिमल संख्या पद्धति (Hexadecimal Number System)

इसमें 16 मूल अंकों का प्रयोग किया जाता है, जिसमें 0 से 9 तक अंक तथा A, B, C, D, E और F अक्षर होते हैं। इसमें बाइनरी अंकों का परिवर्तन चार बाइनरी समूहों में किया जाता है। इससे डाटा स्थानांतरण की गति तेज होती है।

4.1 हेक्साडेसिमल का दशमलव में परिवर्तन (Conversion from Hexadecimal to Decimal)

हेक्साडेसिमल अंकों को उनके स्थानीय मान से गुणा कर जोड़ देते हैं।

उदाहरण : 124₍₁₆₎ को दशमलव में बदलें।
124₍₁₆₎ = (1 * 16²) + (2 * 16¹) + (4 * 16⁰)
= 256 + 32 + 4 = 292₍₁₀₎
अतः 124₍₁₆₎  =292₍₁₀₎

उदाहरण: 1A C₍₁₆₎ को दशमलव में बदलें।

1A C ₍₁₆₎ =(1*16² )+(A*16¹ )+(C*16⁰ )

= (1 * 256) + (10 * 16) + (12 * 1)

= 256 + 160 + 12

= 428₍₁₀₎

4.2. दशमलव का हेक्साडेसिमल में परिवर्तन (Conversion from Decimal to Hexadecimal)

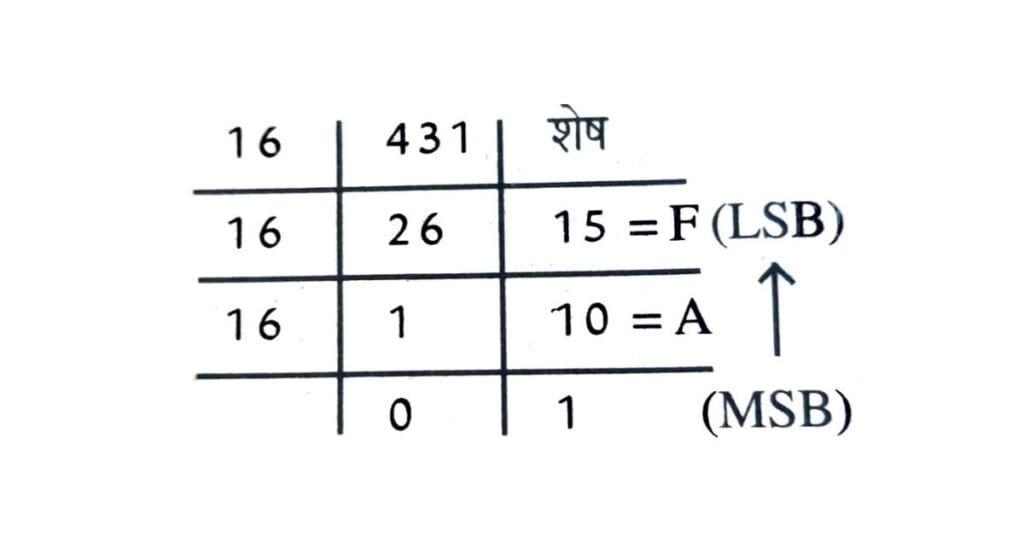
भाग शेष विधि द्वारा
उदाहरण : 431₍₁₀₎ को हेक्साडेसिमल में बदलें।

4.3 हेक्साडेसिमल का बाइनरी में परिवर्तन (Conversion from Hexadecimal to Binary)

उदाहरण : 12D ₍₁₆₎ को बाइनरी में बदलें।

हल : प्रथम विधि : पहले हेक्साडेसिमल को डेसिमल में बदले और फिर डेसिमल को बाइनरी में बदलें।

12D ₍₁₆₎ = (1*16² ) + (2*16¹ ) + (D*16⁰ )
= 1 * 256 + 2 * 16 + 13 * 1
= 256 + 32 + 13
= 301₍₁₀₎

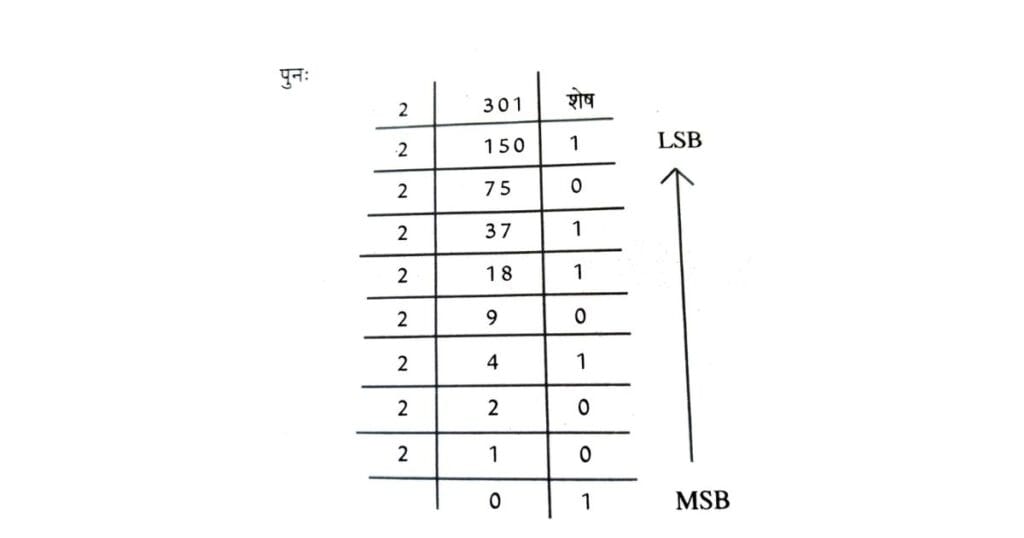
301₍₁₀₎ = 1,0010,1101₍₂₎

दूसरी विधि (संक्षिप्त विधि) : हेक्साडेसिमल अंकों को चार अंकीय बाइनरी तुल्यांक से प्रतिस्थापित कर दिया जाता है।

= 1  2 D

12D (16) = 0001,0010,1101₍₂₎

4.4. बाइनरी का हेक्साडेसिमल में परिवर्तन (Conversion from Binary to Hexadecimal)

उदाहरण : 1011011₍₂₎ को हेक्साडेसिमल में बदलें।

हल : प्रथम विधि : बाइनरी को डेसिमल में बदले और फिर डेसिमल को हेक्साडेसिमल में बदलें।

1011011₍₂₎ = (1 * 2⁶) + (0 * 2⁵) + (1 * 2⁴⁾ (1 * 2³) + (0 * 2²) + (1 * 2¹) (1 * 2⁰)
= 64 + 0 + 16 + 8 + 0 + 2 + 1
= 91₍₁₀₎

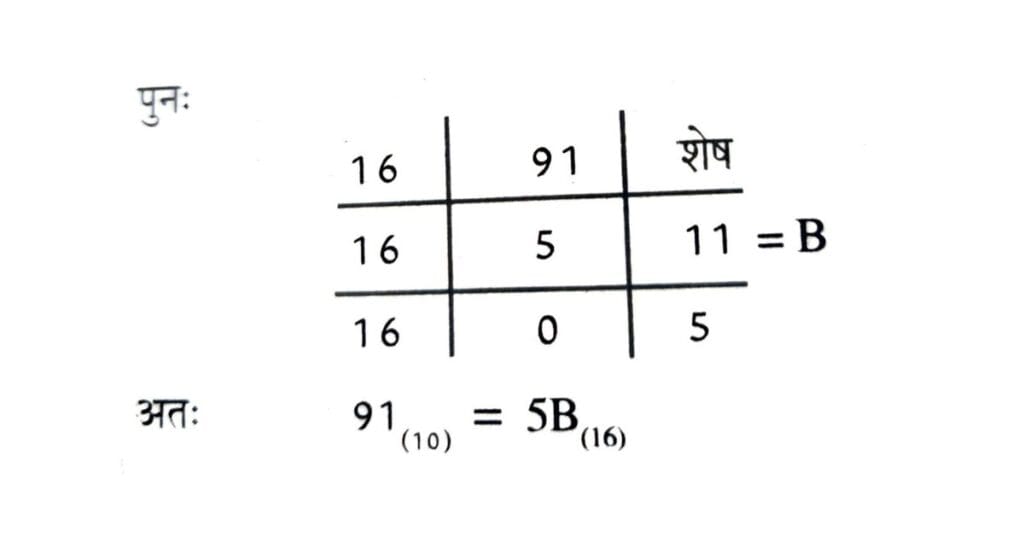
दूसरी विधि (संक्षिप्त विधि) : दायें से प्रारंभ कर बाइनरी अंकों को चार के समूह में विभाजित करते हैं। अंतिम समूह को चार का बनाने के लिए आवश्यकता पड़ने पर बार्थी ओर ‘०’ लिख देते हैं। अब बाइनरी के 4 अंकों के तुल्यांक हेक्साडेसिमल अंक लिख देते हैं।

1011011₍₂₎ = 0101, 1011 

= 5 B = 5B ₍₁₆₎

5. बाइनरी जोड़ (Binary Addition)

बाइनरी जोड़ सामान्य जोड़ की तरह होता है पर इसमें निम्नलिखित जोड़ नियमों को ध्यान में रखा जाता है।

0+0=0

0+1=1

1+0=1

1 + 1 = 0 तथा हासिल (Carry) 1

6. बाइनरी घटाव (Binary Subtraction)

यह साधारण घटाव की तरह होता है जिसमें निम्नलिखित बिन्दुओं को ध्यान में रखा जाता है।

1-1=0

0-0=0

1-0 =1

0 – 1 = 1 (0 द्वारा बायीं ओर से उधार लेने पर वह 10 बन जाता है तथा 10-1 = 1 क्योंकि 1 + 1 = 10 होता है)

7. बाइनरी गुणा (Binary Multiplication)

यह साधारण गुणा की तरह है। लेकिन जोड़ करते समय बाइनरी नियमों का पालन किया जाता है।

0 × 0 = 0

0 × 1 = 0

1 ×  0 = 0

1 ×  1 = 1

8. बाइनरी भाग (Binary Division)

यह साधारण भाग की तरह है लेकिन घटाव करते समय बाइनरी नियमों का पालन किया जाता है।

0 ÷ 1 = 0
1 ÷ 1 = 1

9. बाइनरी मेमोरी (Binary Memory)

बिट (Bit) : यह कम्प्यूटर मेमोरी का सबसे छोटा भाग है। यह बाइनरी डिजिट (Binary digit) का संक्षिप्त रूप है। इसे 0 या 1 (आफ या ऑन) में व्यक्त किया जाता है।

निबल (Nibble) : चार बिट के समूह को निबल कहा जाता है। यह आधे बाइट के बराबर होता है।

बाइट (Byte) : आठ बिट या दो निबल के समूह को एक बाइट कहा जाता है। कम्प्यूटर मेमोरी में किसी अक्षर या कैरेक्टर को दर्शाने के लिए कम से कम आठ बिट अर्थात एक बाइट की जरूरत पड़ती है। एक खाली स्थान (Space) भी 1 बाइट जगह घेरता है।

शब्द की लम्बाई (Word Length): कम्प्यूटर शब्द की लंबाई एक कम्प्यूटर से दूसरे कम्प्यूटर में भिन्न हो सकती है जबकि किसी एक कम्प्यूटर के लिए यह निश्चित होती है। कम्प्यूटर शब्द की लम्बाई कम्प्यूटर के हार्डवेयर पर निर्भर करता है। विभिन्न प्रकार के कम्प्यूटर में शब्द की लंबाई 1 बाइट से 64 बाइट तक हो सकती है।

9.1 कम्प्यूटर मेमोरी की माप

1 निबल = 4 बिट

1 बाइट = 8 बिट = 2 निबल

1 किलोबाइट (KB) = 2¹⁰ बाइट
= 1024 बाइट

1 मेगाबाइट (MB) = 2¹⁰ किलोबाइट
= 1024 किलोबाइट
= 2²⁰ बाइट
= 1024 * 1024 बाइट
= 10 ,48,576 बाइट

1 गीगा बाइट (GB) = 2 ^ 10 मेगाबाइट
= 1024 मेगाबाइट
= 1024 * 1024 किलोबाइट
= 2²⁰ किलोबाइट
= 10 ,48,576 किलोबाइट
= 2³⁰ बाइट
= 1 ,07,37,41,424 बाइट

1 टेराबाइट (TB) = 1024 गीगा बाइट
= 2⁴⁰ बाइट

1024 बाइट = 1 किलो बाइट (KB)

1024 किलो बाइट = 1 मेगा बाइट (MB)

1024 मेगाबाइट = 1 गीगा बाइट (GB)

1024 गीगा बाइट = 1 टेरा बाइट (TB)

10. कम्प्यूटर कोड (Computer Codes)

कम्प्यूटर में डाटा अक्षरों (Alphabets); विशेष चिह्नों (Special Characters) तथा अंकों (Numeric) में हो सकता है। अतः इन्हें अल्फान्युमेरिक डाटा (Alphanumeric Data) कहा जाता है। डाटा में प्रत्येक अक्षर, चिह्न या अंक को एक विशेष कोड द्वारा व्यक्त किया जाता है।

10.1. बाइनरी कोडेड डेसिमल (BCD-Binary Coded Decimal)

इसमें संपूर्ण डेसिमल संख्या को बाइनरी में बदलने की बजाय डेसिमल संख्या के प्रत्येक अंक को उसके चार अंकीय बाइनरी तुल्यांक से प्रतिस्थापित कर दिया जाता है। इसे 4-बिट बीसीडी कोड (4 Bit BCD Code) कहा जाता है।

चूंकि बाइनरी में चार बिट से केवल 2⁴ = 16 चिह्न बनाये जा सकते हैं। इसलिए जोन (Zone) के लिए दो अतिरिक्त बिट जोड़कर 6 बिट बीसीडी कोड बनाया जाता है। इससे कुल 2⁶ = 64 चिह्न बनाये जा सकते हैं जो 26 अक्षरों, 10 संख्याओं और 28 विशेष चिह्नों के लिए प्रयुक्त होते हैं।

10.2. एक्सटेंडेड बाइनरी कोडेड डेसिमल इंटरचेंज कोड (EBCDIC-Extended Binary Coded Decimal Inter-change Code)

बीसीडी में जोन (Zone) के लिए 4 बिट का व्यवहार कर इसे 8 बिट कोड बनाया गया जिसे इबीसीडीआईसी (EBCDIC) कहा गया। इसमें 8 बिट के इस्तेमाल के कारण कुल 28 = 256 कैरेक्टर को निरूपित किया जा सकता है। इसमें तीव्र निरूपण के लिए हेक्साडेसिमल संख्या पद्धति का प्रयोग किया जाता है।

10.3. आस्की (ASCII-American Standard Code for Information Interchange)

आस्की (ASCII) एक लोकप्रिय कोडिंग सिस्टम है जिसका प्रारंभ आन्सी (ANSI-American National Standards Institute) द्वारा 1963 में किया गया। इसमें एक कैरेक्टर के लिए 8 बिट और तीव्र निरूपण के लिए हेक्साडेसिमल संख्या पद्धति का प्रयोग किया गया। कम्प्यूटर के की-बोर्ड में प्रयुक्त प्रत्येक कैरेक्टर के लिए एक विशेष आस्की कोड निर्धारित किया गया है।

10.4. यूनीकोड (Unicode- Universal Code)

कम्प्यूटर के बढ़ते व्यवहार तथा अलग-अलग भाषाओं में कम्प्यूटर के उपयोग ने एक सार्वत्रिक कोड की आवश्यकता को जन्म दिया जिसमें संसार के प्रत्येक कैरेक्टर के लिए एक अलग कोड निर्धारित हो ताकि प्रत्येक भाषा, प्रत्येक प्रोग्राम तथा प्रत्येक साफ्टवेयर में उसका प्रयोग किया जा सके। इसके लिए यूनीकोड की व्यवस्था की गई जिसमें एक लाख कैरेक्टर के निरूपण की क्षमता है। इसमें प्रत्येक कैरेक्टर को 32 बिट में निरूपित किया जाता है। यूनीकोड में तीन प्रकार की व्यवस्था प्रयोग में लायी जाती है-

(i) यूटीएफ-8 (UTF-8- Unicode Transformation Format-8)
(ii) यूटीएफ-16 (UTF-16)
(iii) यूटीएफ-32 (UTF-32)

11. बुलियन अलजेबरा (Boolean Algebra)

बाइनरी संख्या पद्धति में प्रयोग किये जाने वाले गणित, जिसमें केवल दो चर (Variable), 0 और 1 का प्रयोग किया जाता है, बुलियन अलजेबरा कहलाता है। इसका उपयोग कम्प्यूटर में प्रयुक्त लॉजिक सर्किट (Logic Circuit) को सरल बनाने के लिए किया जाता है।

11.1. लॉजिक गेट (Logic Gate)

यह एक इलेक्ट्रानिक परिपथ (Circuit) है जो एक या अधिक इनपुट लेकर मानक आउटपुट देता है। कम्प्यूटर में सभी परिपथ का निर्माण लॉजिक गेट से ही किया जाता है।

यह भी पढ़ें : पर्सनल कम्प्यूटर का विकास (Development of Personal Computer)

FAQs

Q1. कम्प्यूटर की स्मृति सामान्य तौर पर किलोबाइट या मेगाबाइट के रूप में व्यक्त की जाती है। एक बाइट बना होता है-

(a) आठ द्विआधारी अंकों का
(b) आठ दशमलव अंकों का
(c) दो द्विआधारी अंकों का
(d) दो दशमलव अंकों का

Ans. (a)
व्याख्या : कम्प्यूटर मेमोरी का सबसे छोटा भाग बिट (Bit) कहलाता है जो द्विआधारी अंक (Binary Digit) का संक्षिप्त रूप है जिसे 0 या 1 से व्यक्त किया जाता है। आठ बिट के समूह को बाइट (Byte) कहा जाता है जो कम्प्यूटर मेमोरी में किसी एक अक्षर या कैरेक्टर को दर्शाता है। 1024 बाइट एक किलोबाइट के तथा 1024 किलोबाइट एक मेगाबाइट के बराबर होता है।

Q2. एक किलोबाइट बराबर होता है ?

(a) 1000 बाइट्स
(b) 1024 बाइट्स
(c) 1042 बाइट्स
(d) 1 किलोग्राम बाइट्स

Ans. (b)
व्याख्या : कम्प्यूटर मेमोरी को द्विआधारी पद्धति में मापते हैं। इस कारण एक किलोबाइट = 2^10 बाइट = 1024 बाइट होता है।

Q3. बाइनरी च्वाइस में कितने विकल्प होते हैं-

(a) कोई नहीं
(b) एक
(c) दो
(d) कम्प्यूटर में मेमोरी की मात्रा पर निर्भर करता है।
(e) कम्प्यूटर के प्रोसेसर की स्पीड पर निर्भर करता है।

Ans. (c)
व्याख्या : बाइनरी संख्या पद्धति को द्विआधारी संख्या पद्धति भी कहते हैं। इसमें प्रत्येक शब्द या संख्या को 0 या 1 (ऑफ या ऑन) से व्यक्त करते हैं। इस तरह, बाइनरी में कुल दो च्वाइस होते हैं।

Q4. इनमें से कौन कम्प्यूटर में प्रयुक्त अंक पद्धति है-

(a) द्विआधारी (Binary)
(b) आक्टल (Octal)
(c) हेक्साडेसिमल (Hexadecimal)
(d) उपर्युक्त तीनों

Ans. (d)
व्याख्या : हालांकि कम्प्यूटर केवल द्विआधारी अंक पद्धति को समझ सकता है, पर परिवर्तन में सरलता के लिए आक्टल और हेक्साडेसिमल अंक पद्धति का भी प्रयोग किया जाता है।

Q5. बिट (Bit) क्या है ?

(a) एक अंक पद्धति
(b) कम्प्यूटर मेमोरी की छोटी इकाई
(c)एक इनपुट डिवाइस
(d) इनमें से कोई नहीं

Ans. (b)
व्याख्या : बिट (Bit) बाइनरी डिजिट (Binary digit) का संक्षिप्त रूप है। हालांकि बाइनरी एक अंक पद्धति है, पर बिट इसकी सबसे छोटी इकाई है।

Q6. एक बाइट बराबर होता है-

(a) 4 बिट
(b) 6 बिट
(c) 8 बिट
(d) 10 बिट

Ans. (c)
व्याख्या : 8 बिट को मिलाकर 1 बाइट बनता है। 4 बिट मिलकर 1 निबल बनाते हैं।

Q7. कम्प्यूटर मेमोरी की क्षमता को मापते हैं-

(a) बिट
(b) बाइट
(c) मीटर
(d) किलोग्राम

Ans. (b)
व्याख्या : कम्प्यूटर मेमोरी को बाइट में मापते हैं। अधिक मेमोरी को किलोबाइट, मेगाबाइट या टेराबाइट में मापते हैं।

Q8. बिट (Bit) का मतलब है-

(a) बाइनरी डिजिट
(b) बाइनरी नम्बर
(c) कम्प्यूटर एक भाग
(d) इनमें से कोई नहीं

Ans. (a)
व्याख्या : बिट (Bit) बाइनरी डिजिट का संक्षिप्त रूप है जिसे Binary का Bi तथा Digit का t लेकर Bit बनाया गया है।

Q9. प्रत्येक कम्प्यूटर के की-बोर्ड के प्रत्येक कैरेक्टर की ASCII होती है जिसका पूर्ण रूप है-

(a) अमेरिकन स्टॉक कोड फॉर इन्फार्मेशन इंटरचेंज
(b) अमेरिकन स्टैण्डर्ड कोड फॉर इन्फार्मेशन इंटरचेंज
(c) अफ्रीकन स्टॅण्डर्ड कोड फॉर इन्फार्मेशन इंटरचेंज
(d) एडाप्टेबल स्टैंडर्ड कोड फॉर इन्फार्मेशन इंटरचेंज

Ans. (b)
व्याख्या : आस्की (ASCII) का पूर्ण रूप है- अमेरिकन स्टैण्डर्ड कोड फॉर इन्फार्मेशन इंटरचेंज (American Standard Code for Information Interchange) यह अमेरिकन नेशनल स्टैण्डर्डस इंस्टीच्यूट (ANSI) द्वारा जारी एक लोकप्रिय कोडिंग सिस्टम है।

Q10. बाइनरी कोडेड डेसिमल (BCD) में दशमलव अंक 7 का बीसीडी तुल्यांक होगा-

(a) 07
(b) 111
(c) 0111
(d) 1001

Ans. (c)
व्याख्या : बाइनरी कोडेड डेसिमल में किसी संख्या के अंकों को उनके 4 बिट बाइनरी तुल्यांक से प्रतिस्थापित कर दिया जाता है। इससे दशमलव अंक 7 का बाइनरी तुल्यांक 0111 होगा।