अध्याय 7 तथा 8 में हमने वस्तुओं की गति के बारे में तथा बल को गति के कारक के रूप में अध्ययन किया है। हमने सीखा है कि किसी वस्तु की चाल या गति की दिशा बदलने के लिए बल की आवश्यकता होती है। हम सदैव देखते हैं कि जब किसी वस्तु को ऊँचाई से गिराया जाता है तो वह पृथ्वी की ओर ही गिरती है। हम जानते हैं कि सभी ग्रह सूर्य के चारों ओर चक्कर लगाते हैं। चंद्रमा पृथ्वी की परिक्रमा करता है। इन सभी अवस्थाओं में, वस्तुओं पर, ग्रहों पर तथा चंद्रमा पर लगने वाला कोई बल अवश्य होना चाहिए। आइजक न्यूटन इस तथ्य को समझ गए थे कि इन सभी के लिए एक ही बल उत्तरदायी है। इस बल को गुरुत्वाकर्षण बल कहते हैं।
इस अध्याय में हम गुरुत्वाकर्षण तथा गुरुत्वाकर्षण के सार्वत्रिक नियम के बारे में अध्ययन करेंगे। हम पृथ्वी पर गुरुत्वाकर्षण बल के प्रभाव के अंतर्गत वस्तुओं की गति पर विचार करेंगे। हम अध्ययन करेंगे कि किसी वस्तु का भार एक स्थान से दूसरे स्थान पर किस प्रकार परिवर्तित होता है। द्रवों में वस्तुओं के प्लवन की शर्तों के बारे में भी हम विचार-विमर्श करेंगे।
9.1 गुरुत्वाकर्षण
हम जानते हैं कि चंद्रमा पृथ्वी का चक्कर लगाता है। किसी वस्तु को जब ऊपर की ओर फेंकते हैं, तो वह कुछ ऊँचाई तक ऊपर पहुँचती है और फिर नीचे की ओर गिरने लगती है। कहते हैं कि जब न्यूटन एक पेड़ के नीचे बैठे थे तो एक सेब उन पर गिरा। सेब के गिरने की क्रिया ने न्यूटन को सोचने के लिए प्रेरित किया। उन्होंने सोचा कि यदि पृथ्वी सेब को अपनी ओर आकर्षित कर सकती है तो क्या यह चंद्रमा को आकर्षित नहीं कर सकती? क्या दोनों स्थितियों में वही बल लग रहा है? उन्होंने अनुमान लगाया कि दोनों अवस्थाओं में एक ही प्रकार का बल उत्तरदायी है। उन्होंने तर्क दिया कि अपनी कक्षा के प्रत्येक बिंदु पर चंद्रमा किसी सरल रेखीय पथ पर गति नहीं करता वरन् पृथ्वी की ओर गिरता रहता है। अतः वह अवश्य ही पृथ्वी द्वारा आकर्षित होता है। लेकिन हम वास्तव में चंद्रमा को पृथ्वी की ओर गिरते हुए नहीं देखते। आइए चंद्रमा की गति को समझने के लिए क्रियाकलाप 7.11 पर पुनः विचार करें।
क्रियाकलाप 9.1
• धागे का एक टुकड़ा लीजिए। इसके एक सिरे पर एक छोटा पत्थर बाँधिए।
• धागे के दूसरे सिरे को पकड़िए और पत्थर को वृत्ताकार पथ में घुमाइए जैसा कि चित्र 9.1 में दिखाया गया है।
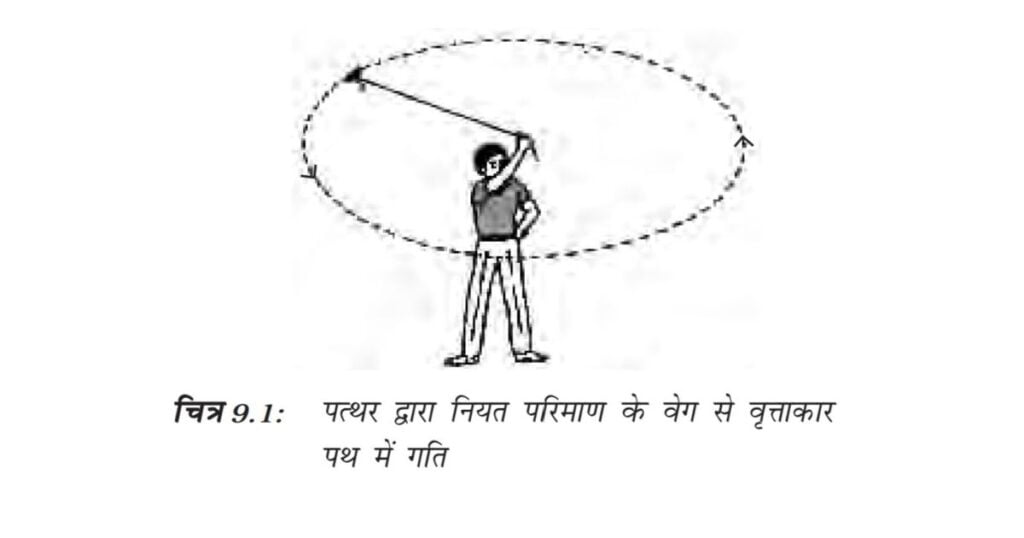
• पत्थर की गति की दिशा को देखिए।
• अब धागे को छोड़िए।
• फिर से पत्थर की गति की दिशा को देखिए।
धागे को छोड़ने से पहले पत्थर एक निश्चित चाल से वृत्ताकार पथ में गति करता है तथा प्रत्येक बिंदु पर उसकी गति की दिशा बदलती है। दिशा के परिवर्तन में वेग-परिवर्तन या त्वरण सम्मिलित है। जिस बल के कारण यह त्वरण होता है तथा जो वस्तु को वृत्ताकार पथ में गतिशील रखता है, वह बल केंद्र की ओर लगता है। इस बल को अभिकेंद्र बल कहते हैं। इस बल की अनुपस्थिति में पत्थर एक सरल रेखा में मुक्त रूप से गतिशील हो जाता है। यह सरल रेखा वृत्तीय पथ पर स्पर्श रेखा होगी।
पृथ्वी के चारों ओर चंद्रमा की गति अभिकेंद्र बल के कारण है। अभिकेंद्र बल पृथ्वी के आकर्षण बल के कारण मिल पाता है। यदि ऐसा कोई बल न हो तो चंद्रमा एकसमान गति से सरल रेखीय पथ पर चलता रहेगा।
यह देखा गया है कि गिरता हुआ सेब पृथ्वी की ओर आकर्षित होता है। क्या सेब भी पृथ्वी को आकर्षित करता है? यदि ऐसा है, तो हम पृथ्वी को सेब की ओर गति करते क्यों नहीं देख पाते?
गति के तीसरे नियम के अनुसार सेब भी पृथ्वी को आकर्षित करता है। लेकिन गति के दूसरे नियम के अनुसार, किसी दिए हुए बल के लिए त्वरण वस्तु के द्रव्यमान के व्युत्क्रमानुपाती होता है [ समीकरण (8.4)]। पृथ्वी की अपेक्षा सेब का द्रव्यमान नगण्य है। इसीलिए हम पृथ्वी को सेब की ओर गति करते नहीं देखते। इसी तर्क का विस्तार यह जानने के लिए कीजिए कि पृथ्वी चंद्रमा की ओर गति क्यों नहीं करती।
हमारे सौर परिवार में, सभी ग्रह सूर्य की परिक्रमा करते हैं। पहले की भाँति तर्क करके हम कह सकते हैं कि सूर्य तथा ग्रहों के बीच एक बल विद्यमान है। उपरोक्त तथ्यों के आधार पर न्यूटन ने निष्कर्ष निकाला कि केवल पृथ्वी ही सेब और चंद्रमा को आकर्षित नहीं करती, बल्कि विश्व के सभी पिंड एक-दूसरे को आकर्षित करते हैं। वस्तुओं के बीच यह आकर्षण बल गुरुत्वाकर्षण बल कहलाता है।
इसे भी जानें
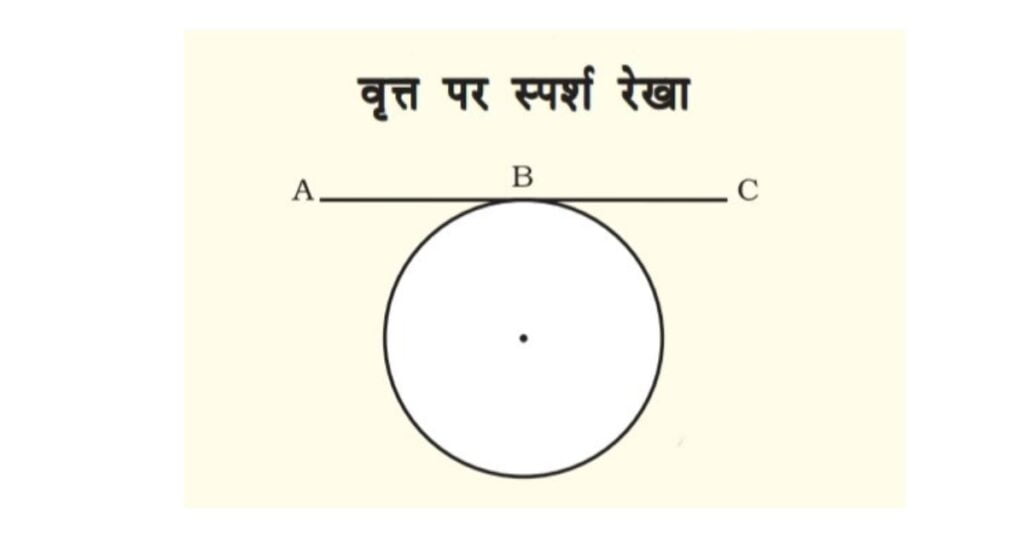
कोई सरल रेखा जो वृत्त से केवल एक ही बिंदु पर मिलती है, वृत्त पर स्पर्श रेखा कहलाती है। इस चित्र में सरल रेखा ABC वृत्त के बिंदु B पर स्पर्श रेखा है।
9.1.1 गुरुत्वाकर्षण का सार्वत्रिक नियम
विश्व का प्रत्येक पिंड प्रत्येक अन्य पिंड को एक बल से आकर्षित करता है, जो दोनों पिंडों के द्रव्यमानों के गुणनफल के समानुपाती तथा उनके बीच की दूरी के वर्ग के व्युत्क्रमानुपाती होता है। यह बल दोनों पिंडों को मिलाने वाली रेखा की दिशा में लगता है।
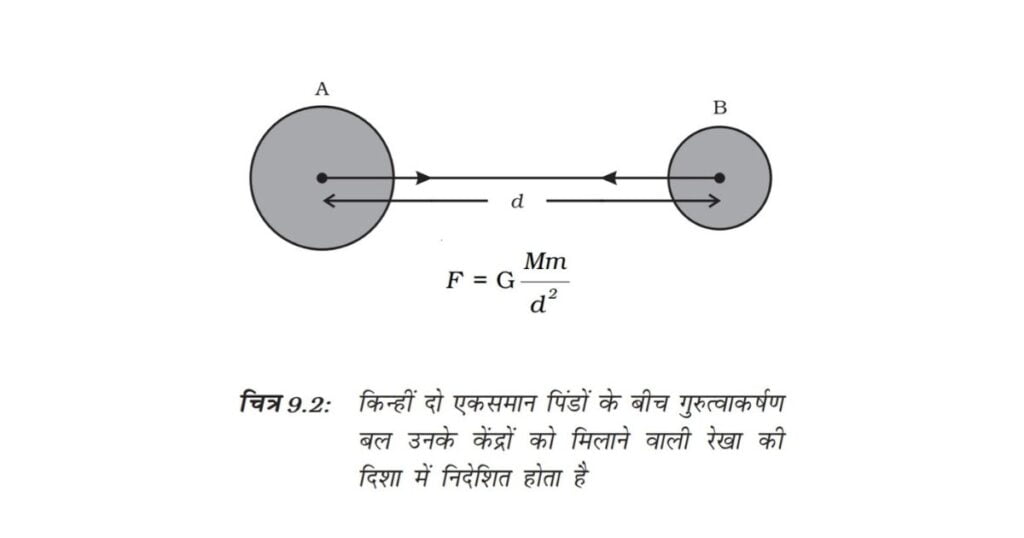
मान लीजिए M तथा द्रव्यमान के दो पिंड A तथा B एक-दूसरे से d दूरी पर स्थित हैं (चित्र 9.2)। मान लीजिए दोनों पिंडों के बीच आकर्षण बल F है। गुरुत्वाकर्षण के सार्वत्रिक नियम के अनुसार, दोनों पिंडों के बीच लगने वाला बल उनके द्रव्यमानों के गुणनफल के समानुपाती है। अर्थात्,
F ∝ M × m (9.1)
तथा दोनों पिंडों के बीच लगने वाला बल उनके बीच की दूरी के वर्ग के व्युत्क्रमानुपाती है, अर्थात्,
F ∝ 1/d² (9.2)
समीकरणों (9.1) तथा (9.2) से हमें प्राप्त होगा
F ∝ (M × m)/d²
या, F = G (M × m)/d²
जहाँ G एक आनुपातिकता स्थिरांक है और इसे सार्वत्रिक गुरुत्वीय स्थिरांक कहते हैं।
वज्र-गुणन करने पर, समीकरण (9.4) से प्राप्त होगा
F × d² = GM × m
या, G = Fd² / M×m (9.5)
समीकरण (9.5) में बल, दूरी तथा द्रव्यमान के मात्रक प्रतिस्थापित करने पर हमें G के SI मात्रक प्राप्त होंगे जो N m² /kg² है।
हैनरी कैवेंडिस (1731-1810) ने एक सुग्राही तुला का उपयोग करके G का मान ज्ञात किया। G का वर्तमान मान्य मान 6.673 x 10-11 N m² /kg² है।
हम जानते हैं कि किन्हीं भी दो वस्तुओं के बीच आकर्षण बल विद्यमान होता है। आप अपने तथा समीप बैठे अपने मित्र के बीच लगने वाले इस बल के मान का अभिकलन कीजिए। निष्कर्ष निकालिए कि आप इस बल का अनुभव क्यों नहीं करते।
उदाहरण 9.1 पृथ्वी का द्रव्यमान 6 x 1024 kg है तथा चंद्रमा का द्रव्यमान 7.4 x 1022 kg है। यदि पृथ्वी तथा चंद्रमा के बीच की दूरी 3.84 x 105 km है तो पृथ्वी द्वारा चंद्रमा पर लगाए गए बल का परिकलन कीजिए। (G = 6.7 x 10-11 N m² /kg²)
हल:
पृथ्वी का द्रव्यमान, M = 6 x 1024 kg
चंद्रमा का द्रव्यमान, m = 7.4 x 1022 kg
पृथ्वी तथा चंद्रमा के बीच की दूरी,
d = 3.84 x 105 km
= 3.84 x 105x1000 m
= 3.84 x 108 m
G = 6.7 x 10-11 N m²/kg²
समीकरण (9.4) से, पृथ्वी द्वारा चंद्रमा पर लगाया गया बल,
F = G (M × m)/d²
= 6.7×10-11 N m²/kg² ×6×1024 kg×7.4×1022 kg/(3.84×108 m)²
= 2.02 x 1020 N
अतः पृथ्वी द्वारा चंद्रमा पर लगाया गया बल 2.02 × 1020 N है।
9.1.2 गुरुत्वाकर्षण के सार्वत्रिक नियम का महत्व
गुरुत्वाकर्षण का सार्वत्रिक नियम अनेक ऐसी परिघटनाओं की सफलतापूर्वक व्याख्या करता है जो असंबद्ध मानी जाती थीं:
(i) हमें पृथ्वी से बाँधे रखने वाला बल;
(ii) पृथ्वी के चारों ओर चंद्रमा की गतिः
(iii) सूर्य के चारों ओर ग्रहों की गतिः तथा
(iv) चंद्रमा तथा सूर्य के कारण ज्वार-भाटा।
9.2 मुक्त पतन
मुक्त पतन का अर्थ जानने के लिए आइए एक क्रियाकलाप करें।
क्रियाकलाप 9.2
• एक पत्थर लीजिए।
• इसे ऊपर की ओर फेंकिए।
• यह एक निश्चित ऊँचाई तक पहुँचता है और तब नीचे गिरने लगता है।
हम जानते हैं कि पृथ्वी वस्तुओं को अपनी ओर आकर्षित करती है। पृथ्वी के इस आकर्षण बल को गुरुत्वीय बल कहते हैं। अतः जब वस्तुएँ पृथ्वी की ओर केवल इसी बल के कारण गिरती हैं, हम कहते हैं कि वस्तुएँ मुक्त पतन में हैं। क्या गिरती हुई वस्तुओं के वेग में कोई परिवर्तन होता है? गिरते समय वस्तुओं की गति की दिशा में कोई परिवर्तन नहीं होता। लेकिन पृथ्वी के आकर्षण के कारण वेग के परिमाण में परिवर्तन होता है। वेग में कोई भी परिवर्तन त्वरण को उत्पन्न करता है। जब भी कोई वस्तु पृथ्वी की ओर गिरती है, त्वरण कार्य करता है। यह त्वरण पृथ्वी के गुरुत्वीय बल के कारण है। इसलिए इस त्वरण को पृथ्वी के गुरुत्वीय बल के कारण त्वरण या गुरुत्वीय त्वरण कहते हैं। इसे से निर्दिष्ट करते हैं। g के मात्रक वही हैं जो त्वरण के हैं, अर्थात् m/s²।
गति के दूसरे नियम से हमें ज्ञात है कि बल द्रव्यमान तथा त्वरण का गुणनफल है। मान लीजिए क्रियाकलाप 9.2 में पत्थर का द्रव्यमान m है। हम पहले से ही जानते हैं कि मुक्त रूप से गिरती वस्तुओं में गुरुत्वीय बल के कारण त्वरण लगता है और इसे g से निर्दिष्ट करते हैं। के बराबर होगा, अर्थात् इसलिए गुरुत्वीय बल का परिमाण F, द्रव्यमान तथा गुरुत्वीय त्वरण के गुणनफल के बराबर होगा, अर्थात्
F = m g (9.6)
समीकरण (9.4) तथा (9.6) से हमें प्राप्त होता है
mg = G (M × m)/d²
या g = G M/d² (9.7)
जहाँ पर M पृथ्वी का द्रव्यमान है तथा d वस्तु तथा पृथ्वी के बीच की दूरी है।
मान लीजिए एक वस्तु पृथ्वी पर या इसकी सतह के पास है। समीकरण (9.7) में दूरी d. पृथ्वी की त्रिज्या R के बराबर होगी। इस प्रकार पृथ्वी की सतह पर या इसके समीप रखी वस्तुओं के लिए
mg = G (M × m)/R² (9.8)
g = G M/R² (9.9)
पृथ्वी एक पूर्ण गोला नहीं है। पृथ्वी की त्रिज्या ध्रुवों से विषुवत वृत्त की ओर जाने पर बढ़ती है, इसलिए g का मान ध्रुवों पर विषुवत वृत्त की अपेक्षा अधिक होता है। अधिकांश गणनाओं के लिए पृथ्वी की सतह पर या इसके पास g के मान को लगभग स्थिर मान सकते हैं लेकिन पृथ्वी से दूर की वस्तुओं के लिए पृथ्वी के गुरुत्वीय बल के कारण त्वरण समीकरण (9. 7) से ज्ञात किया जा सकता है।
9.2.1 गुरुत्वीय त्वरण g के मान का परिकलन
गुरुत्वीय त्वरण के मान का परिकलन करने के लिए हमें समीकरण (9.9) में G, M तथा R के मान रखने होंगे। जैसे,
सार्वत्रिक गुरुत्वीय नियतांक, G = 6.7 × 10-11 N m²/kg²,
पृथ्वी का द्रव्यमान, M = 6 x 1024 kg ,तथा
पृथ्वी की त्रिज्या, R = 6.4 x 106 m
g = G M/R²
= 6.7×10-11 Nm²/ kg²×6×1024 kg/(6.4×106 m)²
= 9.8 m/s²
अतः पृथ्वी के गुरुत्वीय त्वरण का मान g= 9.8 m/s²
9.2.2 पृथ्वी के गुरुत्वीय बल के प्रभाव में वस्तओं की गति
यह समझने के लिए कि क्या सभी वस्तुएँ खोखली ठोस, बड़ी या छोटी, किसी ऊँचाई से समान दर गिरेंगी, आइए एक क्रियाकलाप करें।
क्रियाकलाप 9.3
• कागज की एक शीट तथा एक पत्थर लीजिए।
• दोनों को किसी इमारत की पहली मंजिल से एक साथ गिराइए। देखिए, क्या दोनों धरती पर एक साथ पहुँचते हैं।
• हम देखते हैं कि कागज धरती पर पत्थर की अपेक्षा कुछ देर से पहुँचता है। ऐसा वायु के प्रतिरोध के कारण होता है। गिरती हुई गतिशील वस्तुओं पर घर्षण के कारण वायु प्रतिरोध लगाती है। कागज पर लगने वाला वायु का प्रतिरोध पत्थर पर लगने वाले प्रतिरोध से अधिक होता है।
इस प्रयोग को यदि हम काँच के ज़ार में करें जिसमें से हवा निकाल दी गई है तो कागज तथा पत्थर एक ही दर से नीचे गिरेंगे।
हम जानते हैं कि मुक्त पतन में वस्तु त्वरण का अनुभव करती है। समीकरण (9.9) से, वस्तु द्वारा अनुभव किया जाने वाला यह त्वरण इसके द्रव्यमान पर निर्भर नहीं करता। इसका अर्थ हुआ कि सभी वस्तुएँ खोखली या ठोस, बड़ी या छोटी, एक ही दर से नीचे गिरनी चाहिए। एक कहानी के अनुसार, इस विचार की पुष्टि के लिए गैलीलियो ने इटली में पीसा की झुकी हुई मीनार से विभिन्न वस्तुओं को गिराया।
क्योंकि पृथ्वी के निकट g का मान स्थिर है, अतः एकसमान त्वरित गति के सभी समीकरण, त्वरण a के स्थान पर g रखने पर भी मान्य रहेंगे (देखिए अनुभाग 7.5)। ये समीकरण हैं :
v = u + at (9.10)
s = u t + 1/2 at² (9.11)
v² = u² +2as (9.12)
यहाँ u एवं v क्रमशः प्रारंभिक एवं अंतिम वेग तथा s वस्तु द्वारा । समय में चली गई दूरी है।
इन समीकरणों का उपयोग करते समय, यदि त्वरण (a) वेग की दिशा में अर्थात् गति की दिशा में लग रहा हो तो हम इसको धनात्मक लेंगे। त्वरण (a) को ऋणात्मक लेंगे जब यह गति की दिशा के विपरीत लगता है।
उदाहरण 9.2 एक कार किसी कगार से गिर कर 0.5 s में धरती पर आ गिरती है। परिकलन में सरलता के लिए का मान 10 m/s² लीजिए।
(i) धरती पर टकराते समय कार की चाल क्या होगी?
(ii) 0.5s के दौरान इसकी औसत चाल क्या होगी?
(iii) धरती से कगार कितनी ऊँचाई पर है?
हल: समय, t = 0.5 s
प्रारंभिक वेग, u = 0 m/s
गुरुत्वीय त्वरण, g = 10 m/s²
कार का त्वरण, a = + 10 m/s² (अधोमुखी)
(i) चाल v = at
v = 10 m/s² x 0.5 s
v = 5 m/s
(ii) औसत चाल = (u+v)/2
= (0 m/s+5 m/s)/2
= 2.5 m/s
(iii) तय की गई दूरी, s = ½ a t²
= ½ x 10 m/s² x (0.5 s)²
= ½ x 10 m/s² x 0.25 s²
= 1.25 m
अतः,
(i) धरती पर टकराते समय इसकी चाल = 5 m/s
(ii) 0.5 सेकंड के दौरान इसकी औसत चाल = 2.5 m/s
(iii) धरती से कगार की ऊँचाई = 1.25 m
उदाहरण 9.3 एक वस्तु को ऊर्ध्वाधर दिशा में ऊपर की ओर फेंका जाता है और यह 10 m की ऊँचाई तक पहुँचती है। परिकलन कीजिए
(i) वस्तु कितने वेग से ऊपर फेंकी गई तथा
(ii) वस्तु द्वारा उच्चतम बिंदु तक पहुँचने में लिया गया समय।
हल:
तय की गई दूरी, s = 10 m
अंतिम वेग, v = 0 m/s
गुरुत्वीय त्वरण, = 9.8 m/s²
वस्तु का त्वरण, a = -9.8 m/s² (ऊर्ध्वमुखी)
(i) v² = u²+2as
0 = u² + 2 × (-9.8 m/s²) x 10 m
-u² = -2 × 9.8 × 10 m²/s²
u = √196 m/s
u = 14 m/s
(ii) v = u + at
0 = 14 m/s – 9.8 m/s² × t
t = 1.43 s
अतः,
(i) प्रारंभिक वेग u = 14 m/s
(ii) लिया गया समय t = 1.43 s
9.3 द्रव्यमान
हमने पिछले अध्याय में पढ़ा है कि किसी वस्तु का द्रव्यमान उसके जड़त्व की माप होता है (अनुभाग 8.3)। हमने यह भी सीखा है कि जितना अधिक वस्तु का द्रव्यमान होगा, उतना ही अधिक उसका जड़त्व भी होगा। किसी वस्तु का द्रव्यमान उतना ही रहता है चाहे वस्तु पृथ्वी पर हो, चंद्रमा पर हो या फिर बाह्य अंतरिक्ष में हो। इस प्रकार वस्तु का द्रव्यमान स्थिर रहता है तथा एक स्थान से दूसरे स्थान पर नहीं बदलता।
9.4 भार
हम जानते हैं कि पृथ्वी प्रत्येक वस्तु को एक निश्चित बल से आकर्षित करती है और यह बल वस्तु के द्रव्यमान (m) तथा पृथ्वी के गुरुत्वीय बल के कारण त्वरण (2) पर निर्भर है। किसी वस्तु का भार वह बल है जिससे यह पृथ्वी की ओर आकर्षित होती है।
हमें ज्ञात है कि
F = m x a (9.13)
अर्थात्
F = m × g (9.14)
वस्तु पर पृथ्वी का आकर्षण बल वस्तु का भार कहलाता है। इसे W से निर्दिष्ट करते हैं। इसे समीकरण (9.14) में प्रतिस्थापित करने पर
W = m x g (9.15)
क्योंकि वस्तु का भार एक बल है जिससे यह पृथ्वी की ओर आकर्षित होता है, भार का SI मात्रक वही है जो बल का है, अर्थात् न्यूटन (N)। भार एक बल है जो ऊर्ध्वाधर दिशा में नीचे की ओर लगता है, इसलिए इसमें परिमाण तथा दिशा दोनों होते हैं।
हम जानते हैं कि किसी दिए हुए स्थान पर g का मान स्थिर रहता है। इसलिए किसी दिए हुए स्थान पर, वस्तु का भार वस्तु के द्रव्यमान m के समानुपाती होता है। अर्थात् W ∝ m । यही कारण है कि किसी दिए हुए स्थान पर हम वस्तु के भार को उसके द्रव्यमान की माप के रूप में उपयोग कर सकते हैं। किसी वस्तु का द्रव्यमान प्रत्येक स्थान पर, चाहे पृथ्वी पर या किसी अन्य ग्रह पर, उतना ही रहता है जबकि वस्तु का भार इसके स्थान पर निर्भर करता है क्योंकि g का मान स्थान पर निर्भर करता है।
9.4.1 किसी वस्तु का चंद्रमा पर भार
हमने सीखा है कि पृथ्वी पर किसी वस्तु का भार वह बल है जिससे पृथ्वी उस वस्तु को अपनी ओर आकर्षित करती है। इसी प्रकार, चंद्रमा पर किसी वस्तु का भार वह बल है जिससे चंद्रमा उस वस्तु को आकर्षित करता है। चंद्रमा का द्रव्यमान पृथ्वी की अपेक्षा कम है। इस कारण चंद्रमा वस्तुओं पर कम आकर्षण बल लगाता है।
मान लीजिए किसी वस्तु का द्रव्यमान m है तथा चंद्रमा पर इसका भार W है। मान लीजिए चंद्रमा का द्रव्यमान M m है तथा इसकी त्रिज्या R है।
गुरुत्वाकर्षण का सार्वत्रिक नियम लगाने पर, चंद्रमा पर वस्तु का भार होगा
Wm = G (Mm× m)/R2m (9.16)
मान लीजिए उसी वस्तु का पृथ्वी पर भार W है। पृथ्वी का द्रव्यमान M तथा इसकी त्रिज्या R है।
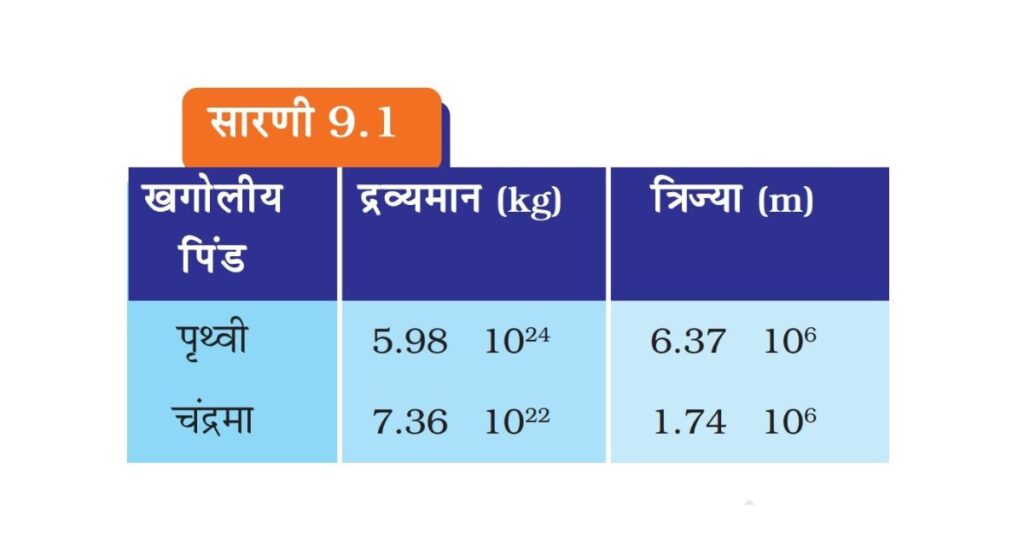
समीकरणों (9.9) तथा (9.15) से हमें प्राप्त होता है,
We = G (M × m)/R2 (9.17)
समीकरण (9.16) तथा (9.17) में सारणी 9.1 से उपयुक्त मान रखने पर
Wm= G × (7.36 ×1022 kg m)/(1.74 × 106 m)²
Wm = 2.431 × 1010 G × m (9.18a)
तथा We = 1.474 * 1011 × G × m (9.18b)
समीकरण (9.18a) को समीकरण (9.18b) से भाग देने पर हमें प्राप्त होता है
Wm/We = (2.431× 1010)/(1.474 × 1011 )
या Wm/We = 0.165 ≈ 1/6 (9.19)
वस्तु का चंद्रमा पर भार /वस्तु का पृथ्वी पर भार = 1/6
वस्तु का चंद्रमा पर भार = (1/6) × इसका पृथ्वी पर भार
उदाहरण 9.4 एक वस्तु का द्रव्यमान 10 kg है। पृथ्वी पर इसका भार कितना होगा?
हल: द्रव्यमान m = 10 kg
गुरुत्वीय त्वरण g = 9.8 m/s²
W = m x g
W = 10 kg x 9.8 m/s² = 98 N
अतः वस्तु का भार 98 N है।
उदाहरण 9.5 एक वस्तु का भार पृथ्वी की सतह पर मापने पर 10N आता है। इसका भार चंद्रमा की सतह पर मापने पर कितना होगा?
हल : हमें ज्ञात है ,चंद्रमा पर वस्तु का भार = (1/6) × पृथ्वी पर इसका भार
अर्थात्,
Wm = We/6 = 10/6 N
= 1.67 N
अतः चंद्रमा की सतह पर वस्तु का भार 1.67 N होगा।
9.5 प्रणोद तथा दाब
क्या कभी आपने सोचा है कि ऊँट रेगिस्तान में आसानी से क्यों दौड़ पाता है? सेना का टैंक जिसका भार एक हजार टन से भी अधिक होता है, एक सतत् चेन पर क्यों टिका होता है? किसी ट्रक या बस के टायर अधिक चौड़े क्यों होते हैं? काटने वाले औजारों की धार तेज़ क्यों होती है?
इन प्रश्नों का उत्तर जानने के लिए तथा इनमें शामिल परिघटनाओं को समझने के लिए दी गई वस्तु पर एक विशेष दिशा में लगने वाले नेट बल (प्रणोद) तथा प्रति एकांक क्षेत्रफल पर लगने वाले बल (दाब) की धारणा से परिचय कराना सहायक होगा। प्रणोद तथा दाब का अर्थ समझने के लिए आइए निम्नलिखित स्थितियों पर विचार करें :
स्थिति 1 : किसी बुलेटिन बोर्ड पर आप एक चार्ट लगाना चाहते हैं जैसा कि चित्र 9.3 में दर्शाया गया है। यह कार्य करने के लिए आपको ड्राइंग पिनों को अपने अँगूठे से दबाना होगा। इस अवस्था में आप पिन के शीर्ष (चपटे भाग) के सतह के क्षेत्रफल पर बल लगाते हैं। यह बल बोर्ड की सतह (पृष्ठ) के लंबवत् लगता है। यह बल पिन की नोक पर अपेक्षाकृत छोटे क्षेत्रफल पर लगता है।

स्थिति 2 : आप शिथिल (ढीले) रेत पर खड़े होते हैं। आपके पैर रेत में गहरे धँस जाते हैं। अब रेत पर लेटिए। आप देखेंगे कि आपका शरीर रेत में पहले जितना नहीं धँसता। दोनों अवस्थाओं में रेत पर लगने वाला बल आपके शरीर का भार है।
आप पढ़ चुके हैं कि भार ऊर्ध्वाधर दिशा में नीचे की ओर लगने वाला बल है। यहाँ बल रेत की सतह के लंबवत् लग रहा है। किसी वस्तु की सतह के लंबवत् लगने वाले बल को प्रणोद कहते हैं।
जब आप शिथिल रेत पर खड़े होते हैं तो बल अर्थात् आपके शरीर का भार, आपके पैरों के क्षेत्रफल के बराबर क्षेत्रफल पर लग रहा होता है। जब आप लेट जाते हैं तो वही बल आपके पूरे शरीर के संपर्क क्षेत्रफल के बराबर क्षेत्रफल पर लगता है जो कि आपके पैरों के क्षेत्रफल से अधिक है। इस प्रकार समान परिमाण के बलों का भिन्न-भिन्न क्षेत्रफलों पर भिन्न-भिन्न प्रभाव होता है। उपरोक्त स्थिति में प्रणोद समान है। लेकिन उसके प्रभाव अलग-अलग हैं। इसलिए प्रणोद का प्रभाव उस क्षेत्रफल पर निर्भर है जिस पर कि वह लगता है।
रेत पर प्रणोद का प्रभाव लेटे हुए की अपेक्षा खड़े होने की स्थिति में अधिक है। प्रति एकांक क्षेत्रफल पर लगने वाले प्रणोद को दाब कहते हैं। इस प्रकार
दाव = प्रणोद/क्षेत्रफल (9.20)
समीकरण (9.20) में प्रणोद तथा क्षेत्रफल के SI मात्रक प्रतिस्थापित करने पर हमें दाब का SI मात्रक प्राप्त होता है। यह मात्रक N/m² है।
वैज्ञानिक ब्लैस पास्कल के सम्मान में, दाब के SI मात्रक को पास्कल कहते हैं, जिसे Pa से व्यक्त किया जाता है।
विभिन्न क्षेत्रफलों पर लगने वाले प्रणोद के प्रभाव को समझने के लिए आइए एक संख्यात्मक उदाहरण पर विचार करें।
उदाहरण 9.6 एक लकड़ी का गुटका मेज पर रखा है। लकड़ी के गुटके का द्रव्यमान 5kg है तथा इसकी विमाएँ 40 cm x 20 cm × 10 cm हैं। लकड़ी के टुकड़े द्वारा मेज पर लगने वाले दाब को ज्ञात कीजिए, यदि इसकी निम्नलिखित विमाओं की सतह मेज पर रखी जाती है: गाती है: (a) 20 cm x 10 cm तथा (b) 40 cm x 20 cm
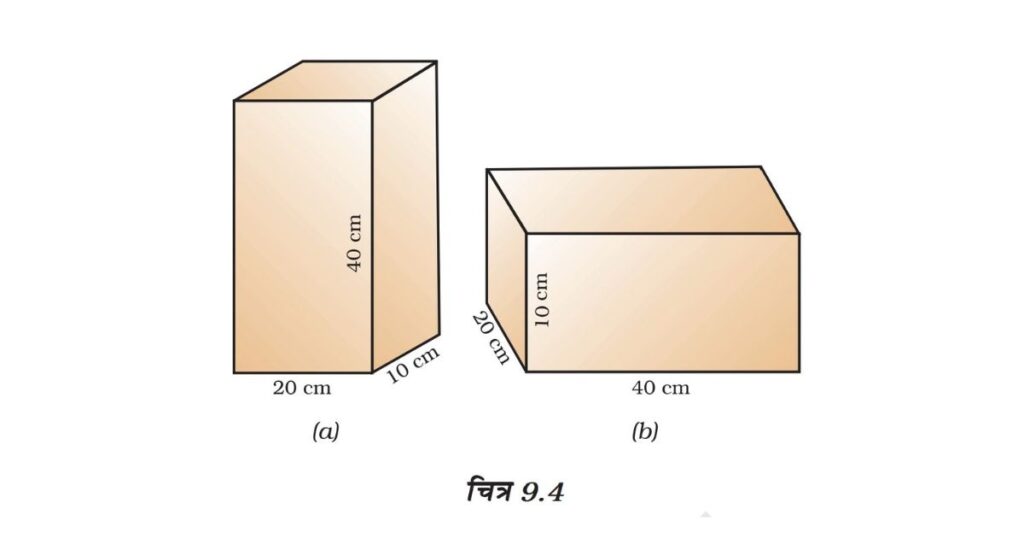
हल : लकड़ी के गुटके का द्रव्यमान = 5 kg
तथा इसकी विमाएँ = 40 cm x 20 cm x 10 cm यहाँ लकड़ी के गुटके का भार मेज की सतह पर प्रणोद लगाता है।
अर्थात्,
प्रणोद = F = m x g
= 5 kg x 9.8 m/s² = 49 N
सतह का क्षेत्रफल = लंबाई × चौड़ाई
= 20 cm x 10 cm
= 200 cm² = 0.02 m²
समीकरण (9.20) से,
दाब = 49 N/0.02m²
= 2450 N/m²
जब गुटके की 40 cm x 20cm विमाओं की सतह मेज पर रखी जाती है, यह मेज की सतह पर पहले जितना ही प्रणोद लगाता है।
क्षेत्रफल = लंबाई × चौड़ाई
= 40 cm x 20 cm
= 800 cm² = 0.08 m²
समीकरण (9.20) से,
दाब = 49 N/0.08 m²
= 612.5 N/m²
सतह 20 cm x 10 cm द्वारा लगाया गया दाब 2450 N/m² है तथा सतह 40 cm x 20 cm द्वारा लगाया गया दाब 612.5 N/m² है।
इस प्रकार वही बल जब छोटे क्षेत्रफल पर लगता है तो अधिक दाब तथा बड़े क्षेत्रफल पर कम दाब लगाता है। यही कारण है कि कीलों के सिरे नुकीले होते हैं, चाकू की तेज़ धार होती है तथा भवनों की नींव चौड़ी होती है।
9.5.1 तरलों में दान
सभी द्रव या गैसें तरल हैं। ठोस अपने भार के कारण किसी सतह पर दाब लगाता है। इसी प्रकार, तरलों में भी भार होता है तथा वे जिस बर्तन में रखे जाते हैं उसके आधार तथा दीवारों पर दाब लगाते हैं। किसी परिरुद्ध द्रव्यमान के तरल पर लगने वाला दाब सभी दिशाओं में बिना घटे संचरित हो जाता है।
9.5.2 उत्प्लावकता
क्या आप कभी किसी तालाब में तैरे हैं और आपने स्वयं कुछ हलका अनुभव किया है? क्या कभी आपने किसी कुएँ से पानी खींचा है और अनुभव किया है कि जब पानी से भरी बाल्टी, कुएँ के पानी से बाहर आती है तो वह अधिक भारी लगती है? क्या कभी आपने सोचा है कि लोहे तथा स्टील से बना जलयान समुद्र के पानी में क्यों नहीं डूबता, लेकिन उतनी ही मात्रा का लोहा तथा स्टील यदि चादर के रूप में हो तो क्या वह डूब जाएगा? इन सभी प्रश्नों का उत्तर जानने के लिए उत्प्लावकता के बारे में जानना आवश्यक है। उत्प्लावकता का अर्थ समझने के लिए आइए एक क्रियाकलाप करें।
क्रियाकलाप 9.4
• प्लास्टिक की एक खाली बोतल लीजिए। बोतल के मुँह को एक वायुरुद्ध डाट से बंद कर दीजिए। इसे एक पानी से भरी बाल्टी में रखिए। आप देखेंगे कि बोतल तैरती है।
• बोतल को पानी में धकेलिए। आप ऊपर की ओर एक धक्का महसूस करते हैं। इसे और अधिक नीचे धकेलने का प्रयत्न कीजिए। आप इसे और अधिक गहराई में धकेलने में कठिनाई अनुभव करेंगे। यह दिखाता है कि पानी बोतल पर ऊपर की दिशा में एक बल लगाता है। जैसे-जैसे बोतल को पानी में धकेलते जाते हैं, पानी द्वारा ऊपर की ओर लगाया गया बल बढ़ता जाता है जब तक कि बोतल पानी में पूरी तरह न डूब जाए।
• अब बोतल को छोड़ दीजिए। यह उछलकर सतह पर वापस आती है।
• क्या पृथ्वी का गुरुत्वाकर्षण बल इस बोतल पर कार्यरत है? यदि ऐसा है तो बोतल छोड़ देने पर पानी में डूबी ही क्यों नहीं रहती? आप बोतल को पानी में कैसे डुबो सकते हैं?
पृथ्वी का गुरुत्वाकर्षण बल बोतल पर नीचे की दिशा में लगता है। इसके कारण बोतल नीचे की दिशा में खिंचती है। लेकिन पानी बोतल पर ऊपर की ओर बल लगाता है। अतः बोतल ऊपर की दिशा में धकेली जाती है। हम पढ़ चुके हैं कि वस्तु का भार पृथ्वी के गुरुत्वाकर्षण बल के बराबर है। जब बोतल डुबोई जाती है तो बोतल पर पानी द्वारा लगने वाला ऊपर की दिशा में बल इसके भार से अधिक है। इसीलिए छोड़ने पर यह ऊपर उठती है।
बोतल को पूरी तरह डुबोए रखने के लिए, पानी के द्वारा बोतल पर ऊपर की ओर लगने वाले बल को संतुलित करना पड़ेगा। इसे नीचे की दिशा में लगने वाले एक बाहरी बल को लगाकर प्राप्त किया जा सकता है। यह बल कम से कम ऊपर की ओर लगने वाले बल तथा बोतल के भार के अंतर के बराबर होना चाहिए।
बोतल पर पानी द्वारा ऊपर की ओर लगने वाला बल उत्प्लावन बल कहलाता है। वास्तव में किसी तरल में डुबोने पर, सभी वस्तुओं पर एक उत्प्लावन बल लगता है। उत्प्लावन बल का परिमाण तरल के घनत्व पर निर्भर है।
9.5.3 पानी की सतह पर रखने पर वस्तुएँ तैरती या डूबती क्यों हैं?
इस प्रश्न का उत्तर प्राप्त करने के लिए आइए निम्नलिखित क्रियाकलाप करें।
क्रियाकलाप 9.5
• पानी से भरा एक बीकर लीजिए।
• एक लोहे की कील लीजिए और इसे पानी की सतह पर रखिए।
• देखिए क्या होता है?
कील डूब जाती है। कील पर लगने वाला पृथ्वी का गुरुत्वाकर्षण बल इसे नीचे की ओर खींचता है। पानी कील पर उत्प्लावन बल लगाता है जो इसे ऊपर की दिशा में धकेलता है। लेकिन कील पर नीचे की ओर लगने वाला बल, कील पर पानी द्वारा लगाए गए उत्प्लावन बल से अधिक है। इसलिए यह डूब जाती है (चित्र 9.5)।

क्रियाकलाप 9.6
• पानी से भरा बीकर लीजिए।
• एक कील तथा समान द्रव्यमान का एक कॉर्क का टुकड़ा लीजिए।
• इन्हें पानी की सतह पर रखिए।
• देखिए क्या होता है।
कॉर्क तैरता है जबकि कील डूब जाती है। ऐसा उनके घनत्वों में अंतर के कारण होता है। किसी पदार्थ का घनत्व, उसके एकांक आयतन के द्रव्यमान को कहते हैं। कॉर्क का घनत्व पानी के घनत्व से कम है। इसका अर्थ है कि कॉर्क पर पानी का उत्प्लावन बल, कॉर्क के भार से अधिक है। इसीलिए यह तैरता है (चित्र 9.5)।
लोहे की कील का घनत्व पानी के घनत्व से अधिक है। इसका अर्थ है कि लोहे की कील पर पानी का उत्प्लावन बल लोहे की कील के भार से कम है। इसीलिए यह डूब जाती है।
इस प्रकार द्रव के घनत्व से कम घनत्व की वस्तुएँ द्रव पर तैरती हैं। द्रव के घनत्व से अधिक घनत्व की वस्तुएँ द्रव में डूब जाती हैं।
9.6 आर्किमीडीज़ का सिद्धांत
क्रियाकलाप 9.7
• एक पत्थर का टुकड़ा लीजिए और इसे कमानीदार तुला या रबड़ की डोरी के एक सिरे से बाँधिए।
• तुला या डोरी को पकड़ कर पत्थर को लटकाइए जैसा कि चित्र 9.6 (a) में दिखाया गया है।
• पत्थर के भार के कारण रबड़ की डोरी की लंबाई में वृद्धि या कमानीदार तुला का पाठ्यांक नोट कीजिए।
• अब पत्थर को एक बर्तन में रखे पानी में धीरे से डुबोइए जैसा कि चित्र 9.6 (b) में दिखाया गया है।
• प्रेक्षण कीजिए कि डोरी की लंबाई में या तुला की माप में क्या परिवर्तन होता है।
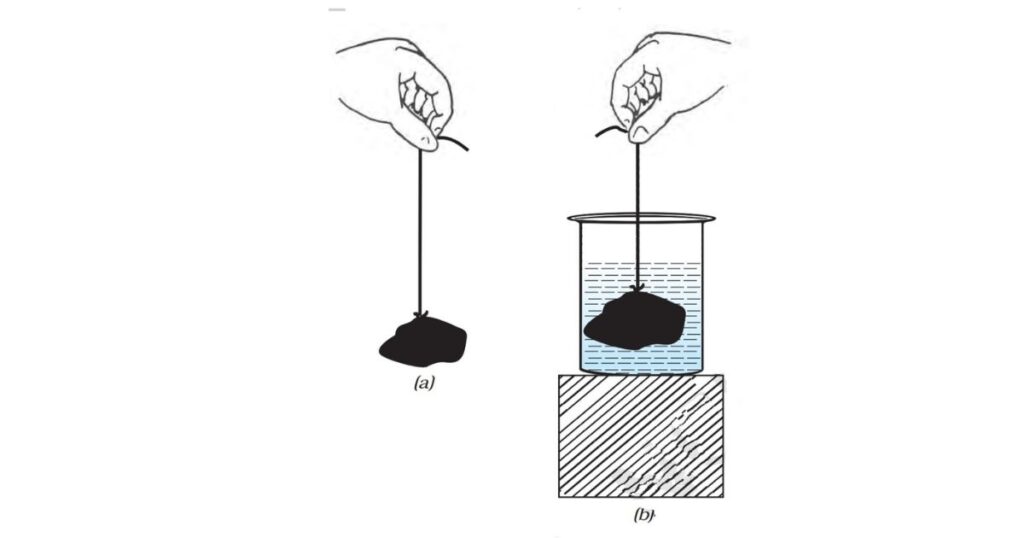
चित्र 9.6: (a) हवा में लटके पत्थर के टुकड़े के भार के कारण रबड़ की डोरी में प्रसार का प्रेक्षण कीजिए।
(b) पत्थर को पानी में डुबोने पर डोरी के प्रसार में कमी आ जाती है
आप देखेंगे कि जैसे ही पत्थर को धीरे-धीरे पानी में नीचे ले जाते हैं, डोरी की लंबाई में या तुला के पाठ्यांक में भी कमी आती है। तथापि, जब पत्थर पानी में पूरी तरह डूब जाता है तो उसके बाद कोई परिवर्तन नहीं दिखाई देता। डोरी के प्रसार या तुला की माप में कमी से आप क्या निष्कर्ष निकालते हैं?
हम जानते हैं कि रबड़ की डोरी की लंबाई में परिवर्तन या तुला के पाठ्यांक में वृद्धि, पत्थर के भार के कारण होती है। क्योंकि पत्थर को पानी में डुबोने पर इन वृद्धियों में कमी आ जाती है, इसका अर्थ है कि पत्थर पर ऊपर की दिशा में कोई बल लगता है। इसके परिणामस्वरूप, रबड़ की डोरी पर लगने वाला नेट बल कम हो जाता है और इसीलिए लंबाई की वृद्धि में भी कमी आ जाती है। जैसी कि पहले ही चर्चा की जा चुकी है, पानी द्वारा ऊपर की ओर लगाया गया यह बल, उत्प्लावन बल कहलाता है।
किसी वस्तु पर लगने वाले उत्प्लावन बल का परिमाण कितना होता है? क्या किसी एक ही वस्तु के लिए यह सभी तरलों में समान होता है? क्या किसी दिए गए तरल में, सभी वस्तुएँ समान उत्प्लावन बल का अनुभव करती हैं? इन प्रश्नों का उत्तर आर्किमीडीज़ के सिद्धांत द्वारा प्राप्त होता है, जिसको निम्न प्रकार से व्यक्त किया जाता है:
जब किसी वस्तु को किसी तरल में पूर्ण या आंशिक रूप से डुबोया जाता है तो वह ऊपर की दिशा में एक बल का अनुभव करती है जो वस्तु द्वारा हटाए गए तरल के भार के बराबर होता है।
क्या अब आप स्पष्ट कर सकते हैं कि क्रियाकलाप 9.7 में पत्थर के पानी में पूरी तरह डूबने के बाद डोरी के प्रसार में और कमी क्यों नहीं हुई थी?
आर्किमीडीज के सिद्धांत के बहुत से अनुप्रयोग हैं। यह जलयानों तथा पनडुब्बियों के डिज़ाइन बनाने में काम आता है। दुग्धमापी, जो दूध के किसी नमूने की शुद्धता की जाँच करने के लिए प्रयुक्त होते हैं तथा हाइड्रोमीटर, जो द्रवों के घनत्व मापने के लिए • प्रयुक्त होते हैं, इसी सिद्धांत पर आधारित हैं।
आर्किमीडीज़ एक ग्रीक वैज्ञानिक थे। उन्होंने एक सिद्धांत की खोज की जो उन्हीं के नाम से विख्यात है। यह सिद्धांत उन्होंने यह देखने के बाद खोजा कि नहाने के टब में घुसने पर पानी बाहर बहने लगता है। वे सड़कों पर यूरेका (Eureka) – यूरेका चिल्लाते हुए भागे, जिसका अर्थ है “मैंने पा लिया है।”
इस ज्ञान का उपयोग उन्होंने राजा के मुकुट में उपयोग हुए सोने की शुद्धता को मापने के लिए किया।
उनके यांत्रिकी तथा ज्यामिति में किए गए कार्यों ने उन्हें प्रसिद्ध कर दिया। उत्तोलक, घिरनी तथा पहिया और धुरी के विषय में उनके ज्ञान ने ग्रीक सेना को रोमन सेना के विरुद्ध लड़ाई में बहुत सहायता की।
आपने क्या सीखा
• गुरुत्वाकर्षण के नियम के अनुसार किन्हीं दो पिंडों के बीच आकर्षण बल उन दोनों के द्रव्यमानों के गुणनफल के समानुपाती तथा उनके बीच की दूरी के वर्ग के व्युत्क्रमानुपाती होता है। यह नियम सभी पिंडों पर लागू होता है चाहे वह विश्व में कहीं भी हों। इस प्रकार के नियम को सार्वत्रिक नियम कहते हैं।
• गुरुत्वाकर्षण एक क्षीण बल है जब तक कि बहुत अधिक द्रव्यमान वाले पिंड संबद्ध न हों।
• गुरुत्वीय बल पृथ्वी तल से ऊँचाई बढ़ने पर कम होता जाता है। यह पृथ्वी तल के विभिन्न स्थानों पर भी परिवर्तित होता है और इसका मान ध्रुवों से विषुवत वृत्त की ओर घटता जाता है।
• किसी वस्तु का भार, वह बल है जिससे पृथ्वी उसे अपनी ओर आकर्षित करती है।
• किसी वस्तु का भार, द्रव्यमान तथा गुरुत्वीय त्वरण के गुणनफल के बराबर होता है।
• किसी वस्तु का भार भिन्न-भिन्न स्थानों पर भिन्न-भिन्न हो सकता है, किंतु द्रव्यमान स्थिर रहता है।
• सभी वस्तुएँ किसी तरल में डुबाने पर उत्प्लावन बल का अनुभव करती हैं।
• जिस द्रव में वस्तुओं को डुबोया जाता है उसके घनत्व से कम घनत्व की वस्तुएँ द्रव की सतह पर तैरती हैं। यदि वस्तु का घनत्व, डुबोए जाने वाले द्रव से अधिक है तो वे द्रव में डूब जाती हैं।
यह भी पढ़ें : बल तथा गति के नियम : अध्याय 8
■ अभ्यास
1. यदि दो वस्तुओं के बीच की दूरी को आधा कर दिया जाए तो उनके बीच गुरुत्वाकर्षण बल किस प्रकार बदलेगा?
Ans. गुरुत्वाकर्षण के नियम के अनुसार, दो वस्तुओं के बीच आकर्षण बलः
F = G Mm/r² … (1)
यदि दूरी को आधा कर दिया जाए तो
F’ = GMm/ (r/2)² … (1)
F’ GMm/(r² /4)
F’ = 4 GMm/r²
F’ = 4F [Using equation (1)]
अतः, वस्तु के बीच दुरी आधा करने पर उनके बीच लगने वाली गुरुत्वाकर्षण बल चार गुना हो जाता है।
2. सभी वस्तुओं पर लगने वाला गुरुत्वीय बल उनके द्रव्यमान के समानुपाती होता है। फिर एक भारी वस्तु हलकी वस्तु के मुकाबले तेज़ी से क्यों नहीं गिरती?
Ans. यदि ‘m’ द्रव्यमान की वस्तु पर गुरुत्वाकर्षण बल है “F” तो
F = G Mm/r²
→ mg= G Mm/r²
→ g = GM/r² (1)
जहाँ
G = सार्वत्रिक गुरुत्वीय स्थिरांक
M = पृथ्वी का द्रव्यमान
r = पृथ्वी की त्रिज्या
समीकरण (1) इससे स्पष्ट है कि g, m पर निर्भर नहीं है। अतः सभी वस्तुएँ समान गति से गिरती हैं, जब उन पर कोई वायु की प्रतिरोधकता न हो।
3. पृथ्वी तथा उसकी सतह पर रखी किसी 1 kg की वस्तु के बीच गुरुत्वीय बल का परिमाण क्या होगा? (पृथ्वी का द्रव्यमान 6 × 1024 kg है तथा पृथ्वी की त्रिज्या 6.4 × 108 m है)।
Ans. वस्तु का द्रव्यमान, (m) = 1 kg
पृथ्वी का द्रव्यमान, (M) = 6 x 1024 kg
पृथ्वी की त्रिज्या (R) = 6.4 x 106 kg
सार्वत्रिक गुरुत्वीय स्थिरांक (G) = 6.7 x 10-11Nm²/kg²
इसलिए 1kg की वस्तु तथा पृथ्वी के बीच गुरुत्वीय बल का परिमाण
F = G Mm/r²
F = 6.7 x 10-11 x 6 x 1024 x 1/ (6.4 x 106)²
F = 6.7 x 6 x 1013/6.4 x 6.4 x 10-12
F = 6.7 x 6 x 10/6.4 x 6.4
F = 9.77
F = 9.8 N (approximately)
4. पृथ्वी तथा चंद्रमा एक-दूसरे को गुरुत्वीय बल से आकर्षित करते हैं। क्या पृथ्वी जिस बल से चंद्रमा को आकर्षित करती है वह बल, उस बल से जिससे चन्द्रमा पृथ्वी को आकर्षित करता है बड़ा है या छोटा है या बराबर है? बताइए क्यों?
Ans. पृथ्वी जिस बल से चंद्रमा को आकर्षित करती है, चंद्रमा भी उतने ही बल से पृथ्वी को आकर्षित करता है क्योंकि न्यूटन के गति के तीसरे नियम के अनुसार क्रिया तथा प्रतिक्रिया बराबर तथा विपरीत दिशा में होती है। अतः पृथ्वी जब गुरुत्वीय बल से चंद्रमा को आकर्षित करती है। तो चंद्रमा भी उतने ही गुरुत्वीय बल से पृथ्वी को विपरीत दिशा (अर्थात् अपनी ओर) में आकर्षित करता है।
5. यदि चंद्रमा पृथ्वी को आकर्षित करता है, तो पृथ्वी चंद्रमा की ओर गति क्यों नहीं करती?
Ans. हम जानते हैं कि चंद्रमा और पृथ्वी एक दूसरे को एक समान बल से आकर्षित करते हैं। चंद्रमा के द्रव्यमान की तुलना में पृथ्वी का द्रव्यमान बहुत अधिक होता है। इसलिए पृथ्वी का त्वरण चंद्रमा के त्वरण से बहुत अधिक होत्ता है। इसलिए पृथ्वी चंद्रमा की ओर गति नहीं करती है।
6. दो वस्तुओं के बीच लगने वाले गुरुत्वाकर्षण बल का क्या होगा, यदि C
(i) एक वस्तु का द्रव्यमान दोगुना कर दिया जाए?
(ii) वस्तुओं के बीच की दूरी दोगुनी अथवा तीन गुनी कर दी जाए?
(iii) दोनों वस्तुओं के द्रव्यमान दोगुने कर दिए जाएँ?
Ans. गुरुत्वाकर्षण बल,
F= G Mm/r² …(1)
(1) यदि वस्तु का द्रव्यमान दोगुना कर दिया जाए
F’ = G Mm/r²
F’ = (G x M x 2m)/r²
F’ = 2 (G Mm)/r²
F’ = 2F {Using (1)}
जब वस्तु का द्रव्यमान दोगुना कर दिया जाए तब गुरुत्वाकर्षण बल दोगुना हो जाएगा।
(ii) यदि वस्तुओं के बीच की दूरी दोगुनी कर दी जाए
F’ = G Mm/(2r)²
F’ = G Mm/4r²
F= F/4 {Using (1)}
इसलिए यदि वस्तुओं के बीच की दूरी दोगुनी कर दी जाए तब गुरुत्वाकर्षण बल 1/4 हो जाएगा।
यदि वस्तुओं के बीच की दूरी दोगुनी कर दी जाए
F’= G Mm/(3r)²
F’ = G Mm/9r²
F’ = F/9 {Using (1))
इसलिए यदि वस्तुओं के बीच की दूरी दोगुनी कर दी जाए तब गुरुत्वाकर्षण बल 1/9 हो जाएगा।
(iii) यदि दोनों वस्तुओं के द्रव्यमान दोगुने कर दिए जाएँ
F’ = G x 2M x 2m/R²
F’ = 4G Mm/R²
F’ = 4F
यदि दोनों वस्तुओं के द्रव्यमान दोगुने कर दिए जाएँ तब बल चार गुना हो जाएगा।
7. गुरुत्वाकर्षण के सार्वत्रिक नियम के क्या महत्व हैं?
Ans. गुरुत्वाकर्षण के सार्वत्रिक नियम कई घटनाओं की व्याख्या की जा सकती है। इनमें से कुछ निम्नलिखित हैं:
• हम पृथ्वी से बंधे रहते हैं।
• चंद्रमा पृथ्वी का चक्कर लगाता है
• पृथ्वी सूर्य का चक्कर लगाती है
• चंद्रमा के कारण ज्वार और भाटा आते हैं
8. मुक्त पतन का त्वरण क्या है?
Ans. मुक्त पतन वह त्वरण है जो किसी वस्तु के पृथ्वी के गुरुत्वीय बल के कारण नीचे गिरने से उत्पन्न होता है। पृथ्वी की सतह के निकट इसका मान 9.8m/s² है।
9. पृथ्वी तथा किसी वस्तु के बीच गुरुत्वीय बल को हम क्या कहेंगे?
Ans. पृथ्वी तथा किसी वस्तु के बीच के गुरुत्वीय बल को वस्तु का भार कहा जाता है।
10. एक व्यक्ति A अपने एक मित्र के निर्देश पर ध्रुवों पर कुछ ग्राम सोना खरीदता है। वह इस सोने को विषुवत वृत्त पर अपने मित्र को देता है। क्या उसका मित्र खरीदे हुए सोने के भार से संतुष्ट होगा? यदि नहीं, तो क्यों? (संकेतः ध्रुवों पर का मान विषुवत वृत्त की अपेक्षा अधिक है।)
Ans. नहीं, 9 का मान ध्रुवों की अपेक्षा विषुवत वृत्त पर कम है। अतः ध्रुवों पर कुछ ग्राम सोने का भार विषुवत वृत्त पर कम होगा। अतः मित्र खरीदे हुए सोने के भार से संतुष्ट नहीं होगा।
या
किसी वस्तु के भार का मान W = mg सूत्र द्वारा ज्ञात किया जाता है। चूंकि द्रव्यमान (m) का मान सभी जगहों पर एक समान रहता है इसलिए सोने के भार का मान ‘g’ पर निर्भर करेगा। इसलिए | WP > We क्योंकि ध्रुवों पर ‘g’ का मान विषुवत वृत्ते की अपेक्षा अधिक है।
अतः उसका मित्र सोने के भार से संतुष्ट नहीं होगा क्योंकि विषुवत वृत्त पर सोने का भार (W) कम हो जाएगा।
जहाँ WP = ध्रुवों पर सोने का भार
We= विषुवत वृत्त पर सोने का भार
11. एक कागज की शीट, उसी प्रकार की शीट को मरोड़ कर बनाई गई गेंद से धीमी क्यों गिरती है?
Ans. कागज़ की शीट उसी प्रकार की गेंद की अपेक्षा अपने अधिक पृष्ठ क्षेत्रफल के कारण अधिक वायु का अधिक प्रतिरोध अनुभव करती है। अतः कागज की शीट उसी प्रकार की शीट की मरोड़कर बनाई गेंद से धीमी गिरती है।
या
कागज की शीट का क्षेत्रफल अधिक होता है जिसके | कारण इस पर लगने वाले वायु प्रतिरोध (Air Resistance) का मान अधिक होता है इसलिए इसकी चाल कम हो जाती है तथा धीमी गिरती है। जबकि उसी प्रकार की शीट को मरोड़ कर बनाई गई गेंद तेजी से गिरती है क्योंकि इसका क्षेत्रफल कम हो जाने के कारण इसके ऊपर लगने वाले वायु प्रतिरोध का मान कम हो जाता है। अतः उसी ऊँचाई से यह तेजी से गिरती है।
12. चंद्रमा की सतह पर गुरुत्वीय बल, पृथ्वी की सतह पर गुरुत्वीय बल की अपेक्षा 1/6 गुणा है। एक 10 kg की वस्तु का चंद्रमा पर तथा पृथ्वी पर न्यूटन में भार क्या होगा?
Ans. वस्तु का द्रव्यमान = 10 kg
पृथ्वी की सतह पर त्वरण = 9.8 m/s²
इसलिए पृथ्वी पर वस्तु का भार = 10 × 9.8 = 98 N
चंद्रमा की सतह पर गुरुत्वीय बल, पृथ्वी की सतह पर गुरुत्वीय बल की अपेक्षा 1/6 गुणा है
अतः वस्तु का चंद्रमा पर भार 1/6 X 98 = 16.3 N
13. एक गेंद ऊर्ध्वाधर दिशा में ऊपर की ओर 49 m/s के वेग से फेंकी जाती है। परिकलन कीजिए
(i) अधिकतम ऊँचाई जहाँ तक कि गेंद पहुँचती है।
(ii) पृथ्वी की सतह पर वापस लौटने में लिया गया कुल समय।
Ans. कार्टिसियन साईन केन्वेंशन में, ऊपर की ओर वेग को धनात्मक तथा गुरुत्वीय त्वरण को ऋणात्मक माना गया है।
(i) u = +49 m/s, g= -9.8 m/s²
अधिकतम ऊँचाई पर, v = 0
गति के तीसरे समीकरण से,
v² – u² = 2 g s
02 – 492 = 2 (-9.8)s
s = 49 x 49/2 x 9.8
s = 122.5 m
अतः गेंद अधिकतम 122.5m ऊँचाई तक पहुँचती है।
(ii) माना पत्थर द्वारा अधिकतम ऊँचाई तक पहुँचने में लिया गया समय t है।
गति के पहले समीकरण से,
v = u + at
0 = 49 + (-9.8)t
9.8t = 49
t = 49/9.8
t = 5s
वस्तु की ऊपर जाने में और नीचे आने में बराबर समय लगता है
अतः पत्थर द्वारा पृथ्वी की सतह पर वापिस लौटने में लिया गया समय = 2t = 2 x 5 = 10s
14. 19.6 m ऊँची एक मीनार की चोटी से एक पत्थर छोड़ा जाता है। पृथ्वी पर पहुँचने से पहले इसका अंतिम वेग ज्ञात कीजिए।
Ans. u = 0, g = 9.8 m/s², s = 19.6 m
गति के तीसरे समीकरण से,
→ v² = u² + 2gs
→ v²- u² = 2gs
→ v²- 0² = 2 x 9.8 x 19.6
v² = 2 x 9.8 x 19.6
v² = 19.6 x 19.6
v = 19.6 m/s
अतः पृथ्वी पर पहुँचने से पहले पत्थर का अंतिम वेग 19.6 m/s हैं।
15. कोई पत्थर ऊर्ध्वाधर दिशा में ऊपर की ओर 40 m/s के प्रारंभिक वेग से फेंका गया है। g = 10 m/s² लेते हुए ग्राफ की सहायता से पत्थर द्वारा पहुँची अधिकतम ऊँचाई ज्ञात कीजिए। नेट विस्थापन तथा पत्थर द्वारा चली गई कुल दूरी कितनी होगी?
Ans. u = 40m/s, g = 10ms²
अधिकतम ऊँचाई s पर अंतिम वेग, v = 0
गति के तीसरे समीकरण से,
v² – u² = 2gs
→ 0²- 402 = 2(-10)s
→ 0²-1600 = -20s
→ -1600 = -20s
→ 1600 = 20s
s = 1600/20
s = 80 m
अतः पत्थर अधिकतम 80m ऊँचाई तक पहुँचता है।
पत्थर वापिस अपने प्रारंभिक स्थान पर आ जाता है।
इसलिए कुल तय की गई दूरी = h + h = 80+80= 160 m
अतः नेट विस्थापन = 80 – 80 = 0 m
16. पृथ्वी तथा सूर्य के बीच गुरुत्वाकर्षण बल का परिकलन कीजिए। दिया है, पृथ्वी का द्रव्यमान = 6 × 1024 kg तथा सूर्य का द्रव्यमान = 2 × 1030 kg! दोनों के बीच औसत दूरी 1.5 × 1011 m है।
Ans.
MEarth = 6 x 1024 kg, Msun = 2 x1030 , R = 1.5 x 1011 m
अतः पृथ्वी एवं सूर्य के मध्य गुरुत्वाकर्षण बल
F= G x Msun x MEarth
F = 6.7 x 10-11 x 2 x 1030 x 6 x 1024 / (1.5 x 1011)²
F = 3.56 x 1022 N
17. कोई पत्थर 100m ऊँची किसी मीनार की चोटी से गिराया गया और उसी समय कोई दूसरा पत्थर 25 m/s के वेग से ऊर्ध्वाधर दिशा में ऊपर की ओर फेंका गया। परिकलन कीजिए कि दोनों पत्थर कब और कहाँ मिलेंगे।
Ans. पहले पत्थर का
आरंभिक वेग, u = 0 m/s
त्वरण, g = 10 m/s² [क्योंकि पत्थर गुरुत्वीय बल की दिशा में जा रहा है।
दूसरे पत्थर का
आरंभिक वेग, u = 25 m/s
त्वरण, g = -10 m/s² (क्योंकि पत्थर गुरुत्वीय बल की विपरीत दिशा में जा रहा है।
माना कि दोनों पत्थर t समय के बाद ऊँचाई ‘h’ पर मिलेंगे।
दूसरे पत्थर के लिए, गति के दूसरे समीकरण से
s = u t + 1/2at²
⇒ h = 25t + 1/2(-10)t²
⇒ h = 25t – 5t² ….(1)
पहले पत्थर द्वारा तय की गई = (100 – h) m
पहले पत्थर के लिए, गति के दूसरे समीकरण से
s = u t + 1/2 at²
100 – h = 0 x t + 1/2 x 10t²
100 – h = 5t² ….(2)
समीकरण (1) और (2) को जोड़ने पर
h + 100 – h = 25t – 5t² + 5t²
100 = 25t
t = 4
समीकरण (1) से
⇒ h = 25t – 5t²
⇒ h=25 x 4 -5(4)²
⇒ h = 100 – 5 x 16
⇒ h = 100 – 80
⇒ h = 20m
अतः दोनों पत्थर 4s के बाद पृथ्वी से 20m की ऊँचाई पर मिलेंगे।
18. ऊर्ध्वाधर दिशा में ऊपर की ओर फेंकी गई एक गेंद 6s पश्चात् फेंकने वाले के पास लौट आती है। ज्ञात कीजिए
(a) यह किस वेग से ऊपर फेंकी गई;
(b) गेंद द्वारा पहुँची गई अधिकतम ऊँचाई; तथा
(c) 4s पश्चात् गेंद की स्थिति।
Ans. कुल समय = 6 s
ऊपर जाने का समय = नीचे की ओर आने का समय = 6/2 = 3 s
(a) ऊर्ध्वाधर दिशा में ऊपर की ओर
गेंद का आरंभिक वेग = u m/s
अधिकतम ऊँचाई पर डेंड़ रुक जाती है, अतः अंतिम वेग, v = 0 m/s
त्वरण, g = 9.8 m/s² [क्योंकि गेंद गुरुत्वीय बल की विपरीत दिशा में जा रहा है।
समय, t = 3 s
गति के पहले समीकरण से,
v = u + g t
⇒ 0 = u + (-9.8 x 3)
⇒ u = 9.8 x 3
⇒ u = 29.4 m/s
(b) माना अधिकतम ऊँचाई = s m,
गति के दूसरे समीकरण से,
s = u t + 1/2 g t
= 29.4 x 3 x 1/2 x (-9.8) x 3
= 88.2 – 44.1
= 44.1m
(c) 3 s बाद अधिकतम ऊँचाई तक पहुँच जाएगी और फिर अगले 1 सेकंड में नीचे की ओर गति करेगी।
गति के दूसरे समीकरण से,
s’ = u’ t + 1/2at²
s = 0 x 1 + 1/2 x 9.8 ×1²
s’ = 4.9 m
3s बाद गेंद की ऊँचाई = अधिकतम ऊँचाई (s) = 1 सेकंड में नीचे की ओर तय की गई दूरी
= 44.1 – 4.9
= 39.2 m
अतः 4 s बाद 40 m की ऊँचाई पर होगी।
19. किसी द्रव में डुबोई गई वस्तु पर उत्प्लावन बल किस दिशा में कार्य करता है?
Ans. वस्तु पर उत्प्लावन बल विस्थापित द्रव के गुरुत्वीय केंद्र में से ऊर्ध्वाधर ऊपर की दिशा में लगता है। इस गुरुत्वीय केंद्र को उत्प्लावन केंद्र कहते हैं।
20. पानी के भीतर किसी प्लास्टिक के गुटके को छोड़ने पर यह पानी की सतह पर क्यों आ जाता है?
Ans. प्लास्टिक के गुटके का घनत्व पानी के घनत्व से कम होता है। इसलिए गुटके पर लगने वाला उत्प्लावन बल गुटके के भार से अधिक होता है। इसलिए गुटका पानी की सतह पर आ जाता है।
21. 50 g के किसी पदार्थ का आयतन 20 cm³ है। यदि पानी का घनत्व 1g/cm³ हो, तो पदार्थ तैरेगा या डूबेगा?
Ans. पदार्थ का द्रव्यमान = 50g
पदार्थ का आयतन = 20cm³
पदार्थ का घनत्व = द्रव्यमान/आयतन
= 50/20
= 2.5 g/cm³
हम जाने है की पानी का घनत्व = 1 g/cm³
अतः पदार्थ का घनत्व पानी के घनत्व से अधिक है, इसलिए पदार्थ पानी में डूबेगा।
22. 500 g के एक मोहरबंद पैकेट का आयतन 350 cm³ है। पैकेट 1 g cm³ घनत्व वाले पानी में तैरेगा या डूबेगा? इस पैकेट द्वारा विस्थापित पानी का द्रव्यमान कितना होगा?
Ans. पैकेट का द्रव्यमान = 500g
पैकेट का आयतन = 350 cm³
पैकेट का घनत्व = द्रव्यमान/आयतन
= 500/300
= 1.428 g/cm³
मोहरबंद पैकेट का घनत्व (1.43 g/cm³) पानी के घनत्व से 1 g/cm³ अधिक है। अतः पैकट डूबेगा।
पेज : 117
1. मुक्त पतन से आप क्या समझते हैं?
Ans. जब कोई वस्तु पृथ्वी की ओर गुरुत्वीय आकर्षण के प्रभाव के कारण गतिशील हो। इसे हम कहते हैं कि वस्तुएँ मुक्त पतन में हैं।
2. गुरुत्वीय त्वरण से आप क्या समझते हैं?
Ans. जब कोई वस्तु पृथ्वी की ओर गिरती है तो पृथ्वी के आकर्षण के कारण वेग के परिणाम में परिवर्तन होता है। वेग में यह परिवर्तन त्वरण उत्पन्न करता है। यह त्वरण पृथ्वी के गुरुत्वीय बल के कारण है, इसलिए, इसे गुरुत्वीय त्वरण कहते हैं।
पेज : 119
1. किसी वस्तु के द्रव्यमान तथा भार में क्या अंतर है?
Ans.
| द्रव्यमान | भार |
| यह वस्तु में निहित पदार्थ की मात्रा है। | यह वह बल है जिस बल से पृथ्वी किसी वस्तु को अपनी ओर आकर्षित करती है। |
| किसी वस्तु का द्रव्यमान सभी जगहों पर स्थिर होता है। | भार गुरुत्वाकर्षण के प्रभाव पर निर्भर करता है तथा भार स्थान के अनुसार बदलता रहता है। |
| द्रव्यमान कभी शून्य नहीं हो सकता। | भार शून्य हो सकता है| (जैसे कि अंतरिक्ष में गुरुत्वाकर्षण किसी वस्तु पर कार्य नहीं करता है तब वस्तु का भार शुन्य होता है) |
| द्रव्यमान एक अदिश राशि है। | उच्च या निम्न गुरुत्व के साथ भार बढ़ता या घटता है |
| सामान्य तराज़ू का उपयोग करके द्रव्यमान मापा जा सकता है। | कमानीदार तराजू ( स्प्रिंग बैलेंस ) का उपयोग करके भार मापा जाता है। |
| द्रव्यमान आमतौर पर ग्राम और किलोग्राम में मापा जाता है। | भार अक्सर न्यूटन में मापा जाता है जो कि बल की इकाई है। |
| इकाई: किलोग्राम (किलो) | इकाई: न्यूटन (एन) |
या
द्रव्यमान
- यह किसी वस्तु में उपस्थित पदार्थ की मात्रा होती है।
- किसी वस्तु का द्रव्यमान उसके जड़त्व की माप होता है।
- यह स्थान के अनुसार नहीं बदलता।
- इसमें केवल परिमाण होता है।
- इसका SI मात्रक किलोग्राम (kg) होता है।
भार
- किसी वस्तु का भार वह बल है जिससे यह पृथ्वी की ओर आकर्षित होती है।
- वस्तु का भार उसके गुरुत्व की माप होता है।
- यह स्थान के अनुसार बदलता रहता है।
- इसमें परिमाण तथा दिशा दोनों होते हैं।
- इसका SI मात्रक वही है जो बल का है, अर्थात् न्यूटन (N)।
2. किसी वस्तु का चन्द्रमा पर भार पृथ्वी पर इसके भार का 1/6 गुणा क्यों होता है?
Ans. चंद्रमा पर किसी वस्तु का भार वह बल है जिससे चंद्रमा उस वस्तु को आकर्षित करता है। चंद्रमा का द्रव्यमान पृथ्वी के द्रव्यमान का 1/100 है और त्रिज्या एक चौथाई। परिणामस्वरूप, पृथ्वी की तुलना में चंद्रमा पर गुरुत्वाकर्षण बल 1/6 होता है। यही कारण है कि किसी वस्तु का चन्द्रमा पर भार पृथ्वी पर इसके भार का 1/6 गुणा होता है।
पेज : 122
1. एक पतली तथा मज़बूत डोरी से बने पट्टे की सहायता से बैग को उठाना कठिन होता है, क्यों?
Ans. क्योंकि पतली डोरी का पट्टा हमारे हाथ पर अधिक बल लगाता है, क्योंकि दबाव उस सतह क्षेत्र पर विपरीत रूप से आनुपातिक होता है, जिस पर बल कार्य करता है। इसलिए हमें बैग को उठाने में कठिनाई होती है।
2. उत्प्लावकता से आप क्या समझते हैं?
Ans. किसी तरल में डुबाने पर तरल द्वारा वस्तु पर ऊपर की ओर लगने वाले बल को उत्पलावन बल तथा इस क्रिया को उत्पलावकता कहा जाता है।
3. पानी की सतह पर रखने पर कोई वस्तु क्यों तैरती या डूबती है?
Ans. (i) द्रव (पानी) के घनत्व से कम घनत्व की वस्तुएँ द्रव (पानी) पर तैरती हैं।
(ii) द्रव (पानी) के घनत्व से अधिक घनत्व की वस्तुएँ द्रव (पानी) में डूब जाती हैं।
या
जब किसी वस्तु का घनत्व किसी द्रव (जैसे-पानी) के घनत्व से कम होता है तो वह वस्तु तैरती है। इस स्थिति में वस्तु पर ऊपर की दिशा में लगाने वाले उत्प्लावन बल का मान वस्तु के भार से अधिक होता है। जब d < d’ तो उत्प्लावन बल U > वस्तु को भार W (वस्तु तैरेगी)
जहाँ, d = वस्तु का घनत्व
d’ = द्रव का घनत्व
इसी प्रकार, जब वस्तु का घनत्व द्रव (जैसे-पानी) के घनत्व से अधिक होता है तो इस स्थिति में वह वस्तु डूब जाती है। क्योंकि उत्प्लावन बल का मान वस्तु के भार से कम होता है।
अर्थात् जब d > d’ तो U < W (वस्तु डूबेगी)
पेज : 124
1. एक तुला (weighing machine) पर आप अपना द्रव्यमान 42 kg नोट करते हैं। क्या आपका द्रव्यमान 42 kg से अधिक है या कम ?
Ans. हमारा द्रव्यमान 42 kg से अधिक है। क्योंकि जब हम किसी तुला पर अपने शरीर के वजन को तोलते है। तब, हमारे शरीर पर वायु द्वारा अपर की दिशा की तरफ लगने वाले उत्प्लावन बल के कारण तुला में हमारा वजन वास्तविक वजन से कुछ कम होता है।
2. आपके पास एक रुई का बोरा तथा एक लोहे की छड़ है। तुला पर मापने पर दोनों 100 kg द्रव्यमान दर्शाते हैं। वास्तविकता में एक-दूसरे से भारी है। क्या आप बता सकते हैं कि कौन-सा भारी है और क्यों?
Ans. रुई का बोरा लोहे की छड़ से भारी है क्योंकि रुई का बोरा वायु द्वारा लगाए गए प्रणोद को लोहे की छड़ पर लगे प्रणोद से अधिक अनुभव करता है। इस प्रकार तुला रुई के बोरे का द्रव्यमान, वास्तविक द्रव्यमान से कम दर्शाती है।

1 thought on “गुरुत्वाकर्षण : अध्याय 9”