समय (Time) के साथ किसी वस्तु के सापेक्ष (Relative to an object) किसी निकाय (Body) की स्थिति (Position) या स्थान (Place) में होने वाले परिवर्तन (Change) को गति (Motion) कहते हैं।
यह ध्यान देने योग्य है कि गति सदा किसी अन्य वस्तु के सापेक्ष ही होती है। आवश्यक नहीं कि कोई वस्तु प्रत्येक वस्तु के सापेक्ष गतिमान हो।
उदाहरण:
यदि कोई व्यक्ति नाव पर बैठकर नदी पार कर रहा है, तो वह नाव के सापेक्ष विरामावस्था (Rest) में होता है, क्योंकि नाव के सापेक्ष उसकी स्थिति समय के साथ नहीं बदलती।
परन्तु वही व्यक्ति नदी के किनारे के सापेक्ष गति की अवस्था में होता है, क्योंकि नदी के किनारे के सापेक्ष समय के साथ उसकी स्थिति बदलती रहती है।
इसी प्रकार, पृथ्वी सूर्य के सापेक्ष गतिशील (Moving) है, परन्तु पृथ्वी पर स्थित वस्तुओं के सापेक्ष स्थिर (At Rest) प्रतीत होती है। अतः हम सामान्यतः पृथ्वी को स्थिर मानकर उसके सापेक्ष सभी वस्तुओं की गति का अध्ययन करते हैं।
➤ विराम की अवस्था (State of Rest)
यदि किसी वस्तु की स्थिति (Position) में समय के साथ उसके परिवेश अथवा किसी संदर्भ बिंदु (Reference Point) के सापेक्ष कोई परिवर्तन नहीं होता, तो उस वस्तु को विराम की अवस्था में कहा जाता है।
वास्तव में ब्रह्माण्ड में कोई भी वस्तु न तो पूर्णतः स्थिर होती है और न ही पूर्णतः गतिमान। वस्तु की गति या विराम का निर्धारण उसके सापेक्ष संदर्भ पर निर्भर करता है। इसलिए गति और विराम दोनों ही सापेक्ष (Relative) संकल्पनाएँ हैं, निरपेक्ष (Absolute) नहीं।
दूरी तथा विस्थापन (Distance and Displacement)
दूरी (Distance) — किसी गतिमान वस्तु द्वारा किसी निश्चित समय में तय किए गए कुल पथ (Path) की लंबाई को उस वस्तु द्वारा चली गई दूरी कहते हैं। दूरी एक अदिश राशि (Scalar Quantity) है।
विस्थापन (Displacement) — किसी गतिमान वस्तु की प्रारम्भिक स्थिति और अंतिम स्थिति के बीच की सबसे छोटी सीधी दूरी, दिशा सहित, को विस्थापन कहते हैं। विस्थापन एक सदिश राशि (Vector Quantity) है।
उदाहरण — मान लीजिए एक वस्तु बिंदु A से B तक 4 मीटर पूरब दिशा में तथा B से C तक 3 मीटर उत्तर दिशा में चलती है।
तब,
- कुल दूरी = AB + BC = 4 + 3 = 7 मीटर
- विस्थापन = AC
अतः विस्थापन = 5 मीटर, उत्तर-पूर्व दिशा में।
निष्कर्ष: दूरी सदैव विस्थापन से अधिक या बराबर होती है।

दूरी एवं विस्थापन का अंतर (संक्षेप में)— दूरी को प्रदर्शित करने के लिए केवल परिमाण की आवश्यकता होती है, क्योंकि यह एक अदिश राशि (Scalar Quantity) है। इसके विपरीत, विस्थापन एक सदिश राशि (Vector Quantity) है, जिसे व्यक्त करने के लिए परिमाण तथा दिशा दोनों आवश्यक होते हैं।
संक्षेप में, दूरी किसी वस्तु द्वारा किसी भी दिशा में तय की गई कुल पथ-लंबाई को दर्शाती है, जबकि विस्थापन वस्तु की प्रारम्भिक एवं अंतिम स्थिति के बीच किसी निश्चित दिशा में हुई न्यूनतम दूरी को दर्शाता है।
महत्वपूर्ण निष्कर्ष—
किसी वस्तु का विस्थापन शून्य हो सकता है, परन्तु दूरी कभी शून्य नहीं होती (यदि वस्तु चली हो)।
उदाहरण— यदि कोई वस्तु उत्तर दिशा में 5 मीटर चलकर उसी मार्ग से वापस अपने प्रारम्भिक स्थान पर आ जाती है, तो
- कुल दूरी = 5 + 5 = 10 मीटर
- विस्थापन = 0 मीटर
चाल तथा वेग (Speed and Velocity)
चाल (Speed)
किसी वस्तु द्वारा एकांक समयान्तराल में तय की गई दूरी को उस वस्तु की चाल कहते हैं।
S.I. पद्धति में चाल का मात्रक = मीटर/सेकेण्ड (m/s)
चाल एक अदिश राशि (Scalar Quantity) है।
वेग (Velocity)
किसी वस्तु द्वारा एकांक समयान्तराल में किया गया विस्थापन उस वस्तु का वेग कहलाता है।
या
किसी निश्चित दिशा में गतिशील वस्तु की स्थिति में परिवर्तन की दर को वेग कहते हैं।
S.I. पद्धति में वेग का मात्रक = मीटर/सेकेण्ड (m/s)
वेग एक सदिश राशि (Vector Quantity) है, क्योंकि इसमें परिमाण तथा दिशा दोनों होते हैं।
निष्कर्ष—
- चाल → केवल दूरी पर निर्भर → अदिश
- वेग → विस्थापन व दिशा पर निर्भर → सदिश
यह अंतर चाल और वेग की मूलभूत समझ के लिए अत्यंत महत्वपूर्ण है।
➤ एक समान तथा असमान चाल (Uniform and Variable Speed)
समान चाल (Uniform Speed)
यदि कोई गतिमान वस्तु समान समयान्तरालों में समान दूरी तय करती है, तो उस वस्तु की चाल को समान चाल कहते हैं।
असमान या परिवर्ती चाल (Non-uniform / Variable Speed)
यदि कोई गतिमान वस्तु समान समयान्तरालों में भिन्न-भिन्न दूरी तय करती है, तो उस वस्तु की चाल को असमान अथवा परिवर्ती चाल कहते हैं।
उदाहरण (परीक्षा हेतु उपयोगी)
- सीधी सड़क पर स्थिर चाल से चलती कार → समान चाल
- शहर में रुक-रुक कर चलती बस → असमान चाल
यह अवधारणा आगे त्वरण (Acceleration) को समझने का आधार बनती है।
➤ औसत तथा तात्कालिक चाल (Average and Instantaneous Speed)
औसत चाल (Average Speed)
किसी गतिमान वस्तु द्वारा एकांक समय में तय की गई कुल दूरी को उस वस्तु की औसत चाल कहते हैं।
अर्थात् वस्तु द्वारा तय की गई कुल दूरी (S) और उस दूरी को तय करने में लगे कुल समय (t) का अनुपात ही औसत चाल कहलाता है।
तात्कालिक चाल (Instantaneous Speed)
किसी निश्चित क्षण (Instant) पर गतिमान वस्तु की चाल को तात्कालिक चाल कहते हैं।
महत्वपूर्ण तथ्य–
- यदि कोई वस्तु समान चाल से गतिमान हो, तो उसकी चाल और औसत चाल समान होती हैं।
- परन्तु व्यवहार में अधिकांश गतिशील वस्तुओं की चाल असमान होती है, इसलिए प्रायः औसत चाल को ही मापा और व्यक्त किया जाता है।
यह अवधारणा आगे तात्कालिक वेग और त्वरण को समझने में सहायक होती है।
➤ एक समान तथा असमान वेग (Uniform and Variable Velocity)
समान वेग (Uniform Velocity)
यदि कोई गतिमान वस्तु किसी निश्चित दिशा में समान समयान्तरालों में समान विस्थापन करती है, तो उस वस्तु का वेग समान वेग कहलाता है।
असमान वेग (Non-uniform / Variable Velocity)
यदि कोई गतिमान वस्तु किसी निश्चित दिशा में समान समयान्तरालों में असमान विस्थापन करती है अथवा उसकी दिशा में परिवर्तन होता है, तो उसका वेग असमान वेग कहलाता है।
महत्वपूर्ण अंतर (परीक्षा हेतु)
- समान चाल में केवल दूरी समान होती है।
- समान वेग में दूरी (विस्थापन) तथा दिशा दोनों समान रहनी चाहिए।
इसलिए वृत्तीय पथ पर समान चाल से चलने वाली वस्तु का वेग असमान होता है।
➤ औसत व तात्कालिक वेग (Average and Instantaneous Velocity)
औसत वेग (Average Velocity)
किसी गतिमान वस्तु द्वारा किसी समयान्तराल में किए गए कुल विस्थापन तथा उस विस्थापन को तय करने में लगे कुल समय के अनुपात को उस वस्तु का औसत वेग कहते हैं।
यदि किसी वस्तु का वेग किसी निश्चित दिशा में समान दर से परिवर्तित हो रहा हो (अर्थात् त्वरण समान हो), तो—
तात्कालिक वेग (Instantaneous Velocity)
किसी क्षण पर, अत्यंत सूक्ष्म समयान्तराल में वस्तु द्वारा किए गए विस्थापन और उस सूक्ष्म समयान्तराल के अनुपात को उस वस्तु का तात्कालिक वेग कहते हैं।
महत्वपूर्ण बिंदु–
- औसत वेग एक सदिश राशि है।
- तात्कालिक वेग किसी विशेष क्षण पर वस्तु की दिशा एवं परिमाण दोनों को दर्शाता है।
➤ सापेक्ष वेग (Relative Velocity)
किसी वस्तु का सापेक्ष वेग दूसरी वस्तु के सापेक्ष उसके विस्थापन में परिवर्तन की दर को कहते हैं।
दूसरे शब्दों में, किसी वस्तु का वेग जब किसी दूसरी वस्तु को स्थिर मानकर निकाला जाता है, तो वह उसका सापेक्ष वेग कहलाता है।
यदि किसी वस्तु A का वेग VA तथा वस्तु B का वेग VB हो, तो—
1. जब दोनों वस्तुएँ एक ही दिशा में गतिमान हों—
(यहाँ = वस्तु B के सापेक्ष वस्तु A का वेग)
2. जब दोनों वस्तुएँ विपरीत दिशाओं में गतिमान हों—
महत्वपूर्ण बिंदु—
- सापेक्ष वेग एक सदिश राशि है।
- रेलगाड़ी, नाव-नदी, वर्षा-छाता जैसे प्रश्नों में सापेक्ष वेग का प्रयोग होता है।
यह अवधारणा गति के व्यावहारिक प्रश्नों को हल करने में अत्यंत उपयोगी है।
गति के प्रकार (Types of Motion)
गति निम्नालिखित प्रकार की होती हैं:
➤ स्थानान्तरीय गति (Translatory Motion)
जिस गति में किसी वस्तु की समय के साथ स्थिति में परिवर्तन होता है तथा वस्तु के सभी कण समान दिशा में समान दूरी तय करते हैं, उसे स्थानान्तरीय गति कहते हैं। इस प्रकार की गति में सामान्यतः गमन-पथ की पुनरावृत्ति नहीं होती।
स्थानान्तरीय गति को निम्न प्रकारों में बाँटा जा सकता है—
1. सरल अथवा ऋजु रेखीय गति (Simple or Straight Line Motion)
जब कोई वस्तु सीधी रेखा में गति करती है, तो उसकी गति को सरल या ऋजु रेखीय गति कहते हैं।
उदाहरण— सीधी सड़क पर चलती कार।
2. अनियमित गति (Irregular Motion)
जब कोई वस्तु असमान समयान्तरालों में असमान दूरी तय करती है या उसकी चाल निरन्तर बदलती रहती है, तो उसे अनियमित गति कहते हैं।
उदाहरण— भीड़ में चलती बस।
3. वक्ररेखीय गति (Curved Motion)
जब कोई वस्तु वक्र पथ पर गति करती है, तो उसकी गति वक्ररेखीय गति कहलाती है।
उदाहरण— फेंकी गई गेंद का पथ।
4. प्रक्षेप्य गति (Projectile Motion)
यदि किसी वस्तु को क्षैतिज या ऊर्ध्वाधर से 0° और 90° के बीच किसी कोण पर फेंका जाए, तो उसका गमन-पथ परवलयाकार (Parabolic) होता है। इस प्रकार की गति को प्रक्षेप्य गति कहते हैं।
इसे द्विविमीय गति (Two-dimensional Motion) भी कहा जाता है।
उदाहरण—
- खिलाड़ी द्वारा फेंका गया हैमर
- टंकी की दीवार के छेद से निकलती जल-धारा
5. ऊर्ध्व गति (Vertical Motion)
जब कोई वस्तु पृथ्वी की सतह या क्षैतिज से 90° का कोण बनाते हुए ऊपर या नीचे की ओर गति करती है, तो उसे ऊर्ध्व गति कहते हैं।
उदाहरण— ऊपर से स्वतंत्र रूप से छोड़ी गई वस्तु की गति।
6. आवर्ती गति (Periodic Motion)
जिस गति में कोई वस्तु समान समयान्तरालों के बाद अपने गमन-पथ को दोहराती है, उसे आवर्ती गति कहते हैं। इस गति में पथ सरल, वक्र या वृत्तीय हो सकता है।
उदाहरण—
- घड़ी के पेण्डुलम की गति
- पृथ्वी की गति
आवर्ती गति को निम्न दो भागों में बाँटा जा सकता है—
(i) दोलन अथवा कम्पनीय गति (Oscillatory / Vibratory Motion)
इस प्रकार की गति में वस्तु अपने मध्य स्थिति के दोनों ओर आगे-पीछे या ऊपर-नीचे गति करती है।
उदाहरण— झूला, सरल लोलक।
(ii) वृत्तीय एवं घूर्णन गति (Circular / Rotatory Motion)
वृत्तीय गति—
जब कोई वस्तु वृत्ताकार पथ पर गति करती है तथा किसी निश्चित बिन्दु से उसकी दूरी सदैव समान रहती है, तो उसकी गति को वृत्तीय गति कहते हैं।
उदाहरण—
- रस्सी से बँधे पत्थर को घुमाना
- चंद्रमा का पृथ्वी के चारों ओर परिभ्रमण
घूर्णन गति—
जब कोई वस्तु अपने अक्ष (Axis) के चारों ओर घूमती है, तो उसकी गति को घूर्णन गति कहते हैं।
उदाहरण— लट्टू की गति, पृथ्वी का अपने अक्ष पर घूमना।
➤ गुरुत्वाधीन गति (Motion Under Gravity)
ऐसी गति जिसमें गुरुत्वाकर्षण बल (Gravitational Force) एक प्रभावी भूमिका निभाता है उसे गुरुत्वाधीन गति कहते हैं। इसके अंतर्गत दोलन गति, ऊर्ध्व गति व प्रक्षेप्य गति इत्यादि आते हैं।
➤ त्वरण (Acceleration)
किसी गतिशील वस्तु के वेग में प्रति सेकण्ड होने वाले परिवर्तन की दर को त्वरण कहते हैं।
जहाँ,
= त्वरण (Acceleration)
= वेग में परिवर्तन
= समयांतराल
त्वरण के प्रकार—
- समान त्वरण (Uniform Acceleration)
यदि किसी वस्तु का वेग समान दर से बढ़ता है, तो इसे समान त्वरण कहते हैं। - वृद्धिमान त्वरण (Increasing / Variable Acceleration)
यदि किसी वस्तु का वेग बढ़ती दर से बढ़ता है, तो इसे वृद्धिमान त्वरण कहते हैं। - ह्रासमान त्वरण (Negative Acceleration / Retardation)
यदि किसी वस्तु का वेग घट रहा हो, तो इसे ह्रासमान त्वरण या मंदन कहते हैं।
महत्वपूर्ण बिंदु—
- त्वरण एक सदिश राशि (Vector Quantity) है, इसलिए इसमें परिमाण और दिशा दोनों होती हैं।
- S.I. मात्रक = मीटर/सेकेण्ड² (m/s²)
➤ गति विषयक समीकरण (Equations of Motion)
इटली के वैज्ञानिक गैलीलियो ने सर्वप्रथम सरल रेखा में चलती वस्तु के लिए समय (t), दूरी (s), वेग (v), प्रारम्भिक वेग (u) और समान त्वरण (a) के बीच समीकरणों के माध्यम से संबंध स्थापित किए। इन समीकरणों को गति के समीकरण (Equations of Motion) कहते हैं।
यदि कोई वस्तु प्रारम्भिक वेग u, समान त्वरण a के साथ गति करती है, और 1 सेकण्ड में दूरी s तय करती है, तो इन राशियों के बीच सम्बन्ध निम्न हैं—
1. अंतिम वेग (Final Velocity)
2. दूरी (Displacement)
3. अंतिम वेग और दूरी के बीच सम्बन्ध
4. tवें सेकेंड में वस्तु द्वारा तय की गई दूरी
5. औसत वेग (Average Velocity)
महत्वपूर्ण बिंदु—
- ये समीकरण समान त्वरण वाले रेखीय गति के लिए मान्य हैं।
- इन्हें प्रश्नों में अज्ञात राशि निकालने, समीकरणों के अनुप्रयोग, और गतिशील वस्तुओं की समस्याएँ हल करने के लिए उपयोग किया जाता है।
यदि चाहें तो मैं इसे संक्षिप्त सारणी, उदाहरण सहित, या चित्र/ग्राफ के साथ समझा सकता हूँ, जिससे याद रखना आसान हो।
➤ गुरुत्वीय त्वरण (Acceleration due to Gravity)
जब किसी वस्तु की गति ऊर्ध्वाधर दिशा में होती है और वह पृथ्वी के गुरुत्वाकर्षण क्षेत्र में आती है, तो उस पर गुरुत्वीय बल (Gravitational Force) प्रभावी रूप से कार्य करता है। इसके कारण वस्तु में त्वरण उत्पन्न होता है, जिसे गुरुत्वीय त्वरण (g) कहते हैं।
मुख्य बिंदु—
- इसे अक्षर g से प्रदर्शित किया जाता है।
- दिशा हमेशा पृथ्वी के केंद्र की ओर अर्थात् ऊर्ध्वतः नीचे होती है।
गुरुत्वीय त्वरण का उपयोग गति के समीकरणों में
- यदि कोई वस्तु ऊर्ध्वाधर दिशा में नीचे गिर रही हो, तो उस पर कार्यकारी गुरुत्वीय त्वरण +g होता है।
- अतः समान त्वरण वाले रेखीय गति के समीकरणों में a की जगह g प्रतिस्थापित किया जा सकता है।
- यदि कोई वस्तु ऊर्ध्व दिशा में ऊपर जा रही हो, या उसके गति पर मंदन (-a) कार्य कर रहा हो, तो—
- गति के समीकरणों में a की जगह -a
- ऊर्ध्वाधर गति के समीकरणों में g की जगह -g
महत्वपूर्ण बिंदु—
- गुरुत्वीय त्वरण एक सदिश राशि (Vector Quantity) है।
- S.I. मात्रक = m/s²
- पृथ्वी पर मानक मान = g ≈ 9.8 m/s²
यह अवधारणा ऊर्ध्वाधर प्रक्षेप्य गति, गिरती वस्तु, और ऊपर फेंकी गई वस्तु से संबंधित प्रश्नों के लिए आधारभूत है।
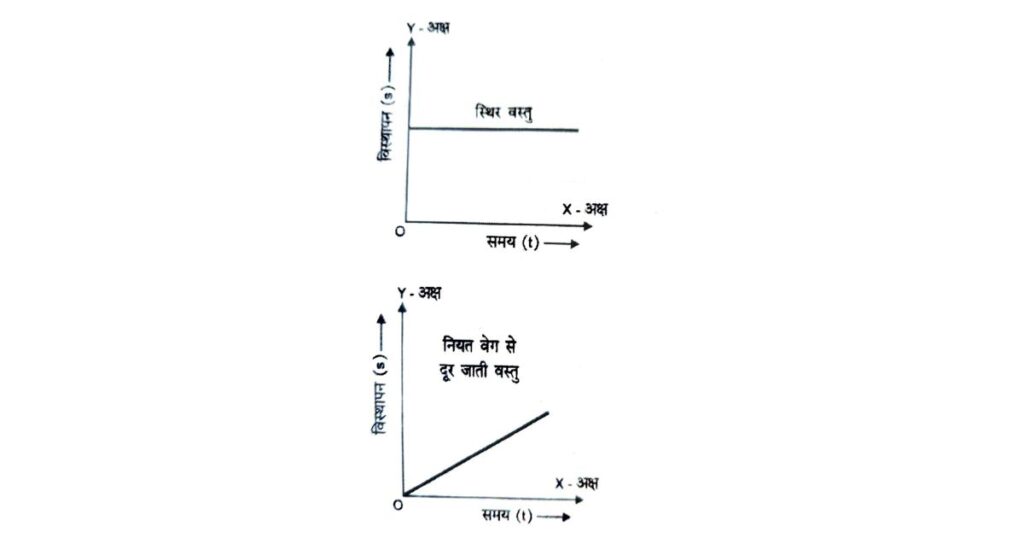
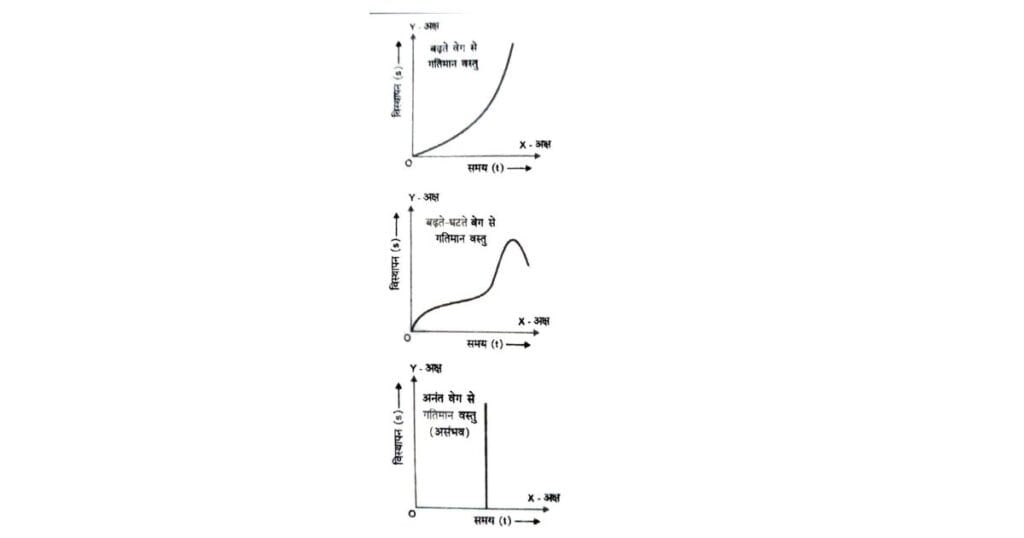
➤ गति विषयक ग्राफ (Motion Related Graph)
जब किसी गतिशील पिण्ड के विस्थापन (Displacement), वेग (Velocity), त्वरण (Acceleration) आदि को समय के साथ रेखाचित्र (Graph) के माध्यम से प्रदर्शित किया जाता है, तो इसे गति विषयक ग्राफ कहते हैं।
महत्वपूर्ण लाभ—
- गति और इसके निर्धारकों के बीच संबंधों को स्पष्ट रूप से समझना आसान हो जाता है।
- गणनाएँ और समीकरणों का अनुप्रयोग सरल हो जाता है।
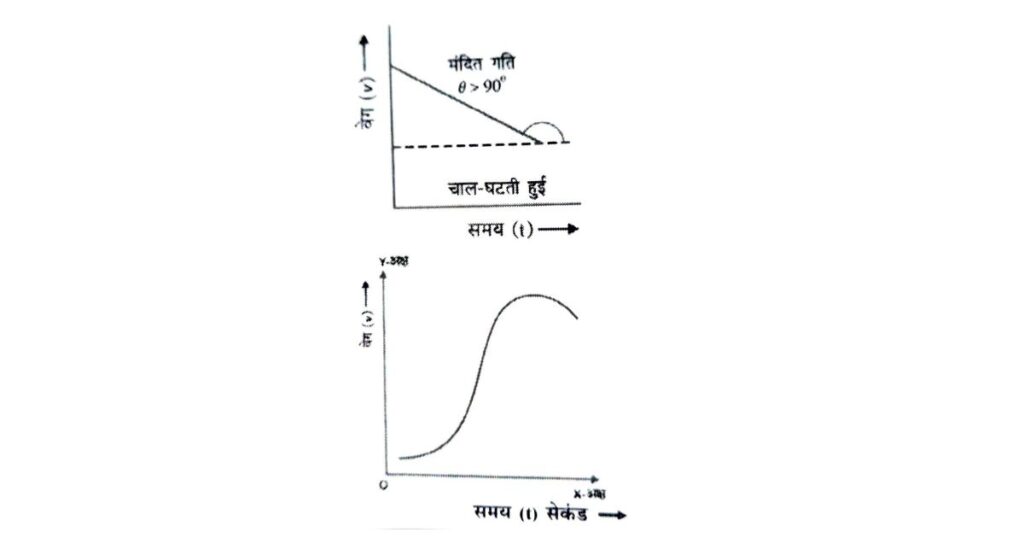
समय वेग (time-velocity) संबंधी

यह भी पढ़ें : मापन

1 thought on “गति (Motion)”