U.P Board Class 10 Math 822 IA Question Paper 2024

U.P Board Class 10 Math 822 IA Question Paper 2024 का उत्तर आप यहाँ से प्राप्त कर सकते हैं। जिसका कोई भी शुल्क आपसे नहीं लिया जायेगा। आइये विस्तार से सभी प्रश्नो को जानते हैं।

सत्र – 2024
गणित
समय: तीन घण्टे 15 मिनट  पूर्णांक: 70

नोट : प्रारम्भ के 15 मिनट परीक्षार्थियों को प्रश्नपत्र पढ़ने के लिए निर्धारित हैं।

निर्देश: i) सभी प्रश्न अनिवार्य हैं।

ii) इस प्रश्नपत्र के ‘अ’ और ‘ब’ दो खण्ड हैं।

iii) खण्ड ‘अ’ में 1 अंक के 20 बहुविकल्पीय प्रश्न हैं जिनके उत्तर ओ० एम० आर० उत्तर पत्रक पर नीले अथवा काले बाल प्वाइंट कलम से सही विकल्प वाले गोले को पूर्ण रूप से काला कर चिह्नित करें ।

iv) ओ०एम०आर० उत्तर पत्रक पर उत्तर अंकित किए जाने के पश्चात उसे नहीं काटें तथा इरेजर, ह्वाइटनर आदि का प्रयोग न करें।

v) खण्ड ‘ब’ में 50 अंक के वर्णनात्मक प्रश्न हैं।

vi) इस खण्ड में कुल 5 प्रश्न हैं।

vii) प्रत्येक प्रश्न के आरम्भ में स्पष्टतः लिख दिया गया है कि उसके कितने खण्ड करने हैं।

viii) प्रश्न के अंक उनके सम्मुख अंकित हैं।

ix) प्रथम प्रश्न से आरम्भ कीजिए और अन्तिम प्रश्न तक करते जाइए। जो प्रश्न न आता हो उस पर समय नष्ट न कीजिए।

x) यदि रक्त कार्य के लिए स्थान अपेक्षित है तो उत्तर-पुस्तिका के बाएँ पृष्ठ पर कीजिए और फिर काट (x) दीजिए। उस पृष्ठ पर कोई हल न कीजिए।

xi) रचना के प्रश्नों के हल में रचना रेखाएँ न मिटाइए। यदि पूछा गया हो तो रचना के पद संक्षेप में अवश्य लिखिए।

xii) जिन प्रश्नों के हल में चित्र खींचना आवश्यक है, उनमें स्वच्छ एवं शुद्ध चित्र अवश्य खींचिए। बिना चित्र के ऐसे हल अपूर्ण और अशुद्ध माने जायेंगे।

खण्ड अ

(बहुविकल्पीय प्रश्न)

1. किसी वृत्त पर एक बाह्य बिन्दु से खींची जाने वाली स्पर्श रेखाओं की अधिकतम संख्या होगी-

(A) एक
(B) दो
(C) तीन
(D) चार

Ans. (B) दो

2. बिन्दु (7,3) की y-अक्ष से दूरी होगी-

(A) 3
(B) 7/2
(C) 7
(D) 8

Ans. (C) 7

3. यदि p sin θ  = q cos θ तो cosec θ का मान होगा-

(A) (√(p² + q²))/q
(B) (√(p² + q²))/p
(C) p/(√(p² + q²))
(D) q/(√(p² + q²))

Ans. (A) (√(p² + q²))/q

4.  tan 1° tan 2° tan 3° … tan 88° tan 89°* का मान होगा-

(A) 0
(B) 1/(√2)
(C) 1/2
(D) 1

Ans. (A) 0

5. यदि समीकरण 3x² + 5x – q = 0 के मूल बराबर हैं, तो q का मान होगा-

(A) – 25/12
(B) – 25/9
(C) 9/25
(D) – 12/25

Ans. (A) – 25/12

6. समान्तर श्रेढ़ी -62,-59,… 7, 10 का ग्यारहवाँ पद होगा-

(A) -34
(B) -32
(C) -30
(D) -28

Ans. (C) -30

7. यदि P(E) = 0.05 तो P(E) का मान होगा-

(A) 0.92
(B) 0.93
(C) 0.94
(D) 0.95

Ans. यहाँ $P(E) = 0.05$ दिया है।

किसी घटना के पूरक (Complement) का प्रायिकता सूत्र होता है:$$P(\overline{E}) = 1 – P(E)$$

तो,$$P(\overline{E}) = 1 – 0.05 = 0.95$$

8. एक थैले में 3 लाल और 5 काली गेंदें हैं। इस थैले में एक गेंद यादृच्छया निकाली जाती है। गेंद के लाल होने की प्रायिकता होगी-

(A) 3/8
(B) 5/8
(C) 3/5
(D) 1/2

Ans. (A) 3/8

9. चित्र में DE| | BC, तो CE की माप होगी-

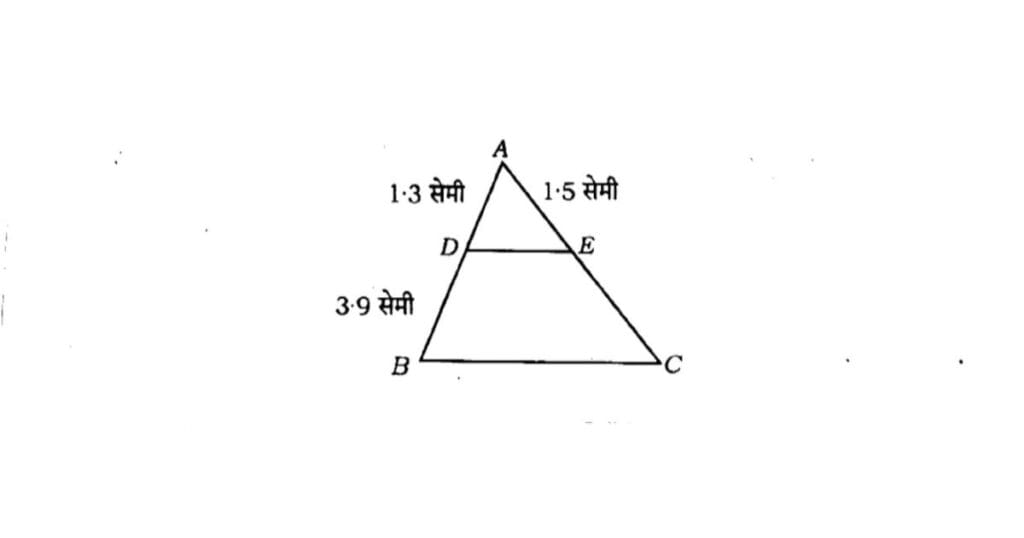
A) 5.5 सेमी
(B) 5.0 सेमी
(C) 4.8 सेमी
(D) 4.5 सेमी

Ans. (B) 5.0 सेमी

10. चित्र में ∆MNL तथा ∆PQR में ∠M= ∠Q = 70°, MN = 3 सेमी, ML = 4.5 सेमी, PQ = 2 सेमी तथा QR = 3 सेमी, तो निम्नलिखित में सही होगा-

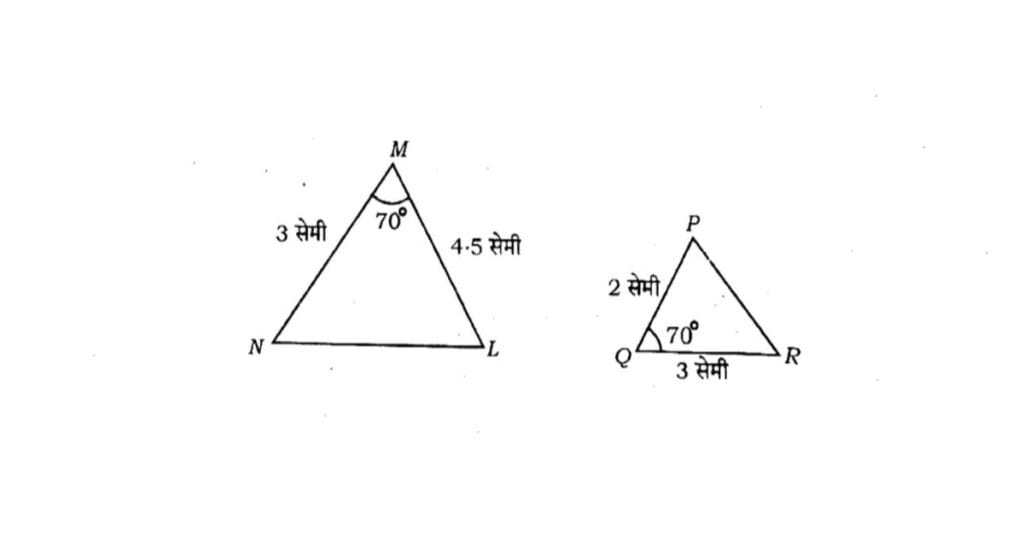
A) ∆NML – ∆QPR
(B) ∆NML – ∆ORP
(C) ∆NML – ∆POR
(D) इनमें से कोई नहीं

Ans. (D) इनमें से कोई नहीं

11. 1/2 सेमी व्यास के गोले का पृष्ठ होगा-

(A) π/2 सेमी 2
(B) π/4 सेमी 2
(C) π/3 सेमी 2
(D) π सेमी 2

Ans. (B) π/4 सेमी 2

12. 6 सेमी त्रिज्या के वृत्त का एक चाप केन्द्र पर 30° का कोण अन्तरित करता है। संगत चाप की माप होगी-

(A) π/4 सेमी
(B) π/3 सेमी
(C) π/2 सेमी
(D) π सेमी

Ans. (A) π/4 सेमी

13. 5 सेमी त्रिज्या के एक वृत्त के बिंदु पर खींची गयी स्पर्श रेखा PQ, केन्द्र O से जाने वाली एक रेखा से बिंदु Q पर मिलती है। यदि OQ = 12 सेमी, तो PQ की माप होगी-

(A) 12 सेमी
(B) 13 सेमी
(C) 8.5 सेमी
(D) √119 सेमी

Ans. (D) √119 सेमी

14. संख्याओं 182 तथा 78 का HCF होगा-

(A) 13
(B) 26
(C) 28
(D) 39

Ans. (B) 26

15. एक बेलन के आधार की त्रिज्या 3.5 सेमी है। यदि उसकी ऊँचाई 8.4 सेमी हो, तो उसका वक्रपृष्ठीय क्षेत्रफल होगा

(A) 54.8 सेमी²
(B) 56.4 सेमी²
(C) 56.6 सेमी²
(D) 58.8 सेमी²

Ans. (D) 58.8 सेमी²

16. 4 सेमी त्रिज्या वाले एक वृत्त के त्रिज्यखण्ड का कोण 60° है। उसका क्षेत्रफल होगा-

(A) 6 π सेमी²
(B) 8 π सेमी²
(C) 8/3 π सेमी²
(D) 3 π सेमी²

Ans. (C) 8/3 π सेमी²

17. द्विघात समीकरण x² + x – 1 = 0 का विविक्तकर होगा-

(A) -4
(B) -5
(C) 4
(D) 2

Ans. (C) 4

18. द्विघात समीकरण 1 – 4x + 4x² = 0 के मूलों का योगफल होगा-

(A) -2
(B) -1
(C) 1
(D) 2

Ans. (D) 2

19. निम्नलिखित सारिणी से माध्य होगा-

(A) 24-62
(B) 26-66
(C) 28-64
(D) 30-50

Ans. (B) 26-66

20. निम्नलिखित सारिणी का माध्यक वर्ग होगा-

A) 10-20
(B) 20-30
(C) 30-40
(D) 40-50

Ans. (B) 20-30

खण्ड ब

(वर्णनात्मक प्रश्न)

1. सभी खण्ड कीजिए:

(a) यदि बिन्दु (x, 5) तथा (2,-3) के बीच की दूरी 17 मात्रक है. x तो का मान ज्ञात कीजिए।
Ans. दिया है:
दो बिन्दु हैं A(x, 5) और B(2, −3)
इनके बीच की दूरी = 17 मात्रक

दूरी सूत्र:

$$\sqrt{(x_2-x_1)^2 + (y_2-y_1)^2}$$

मान रखने पर:

$$\sqrt{(2-x)^2 + (-3-5)^2} = 17$$$$\sqrt{(2-x)^2 + (-8)^2} = 17$$$$\sqrt{(2-x)^2 + 64} = 17$$

दोनों तरफ वर्ग करें:

$$(2-x)^2 + 64 = 289$$$$(2-x)^2 = 225$$$$2-x = \pm 15$$

केस 1:

$$2-x = 15 \Rightarrow x = -13$$

केस 2:

$$2-x = -15 \Rightarrow x = 17$$

$$\boxed{x = 17 \text{ या } x = -13}$$

(b) यदि बिन्दु (1, 4), (a,-2) और (-3, 16) सरेख है, तो a का मान ज्ञात कीजिए।
Ans. दिए गए बिन्दु हैं:
$A(1,4),\; B(a,-2)$ और $C(-3,16)$

तीनों बिन्दु सरेख हैं, अतः
AB की ढाल = BC की ढाल

ढाल (Slope) का सूत्र:

AB की ढाल:

$$m_{AB}=\frac{-2-4}{a-1}=\frac{-6}{a-1}$$

BC की ढाल:

$$m_{BC}=\frac{16-(-2)}{-3-a}=\frac{18}{-3-a}$$​

सरेख होने की शर्त:

$$\frac{-6}{a-1}=\frac{18}{-3-a}$$

क्रॉस गुणा करने पर:$$-6(-3-a)=18(a-1)$$ $$18+6a=18a-18$$$$36=12a$$ $$a=3$$

(c) सिद्ध कीजिए: (1+ sin θ)/cos θ + cos θ/(1+sinθ) = 2sec θ
Ans. सिद्ध करना है :$$\frac{1+\sin \theta}{\cos \theta}+\frac{\cos \theta}{1+\sin \theta}=2\sec \theta$$

LHS से प्रारम्भ करते हैं:

$$\frac{1+\sin \theta}{\cos \theta}+\frac{\cos \theta}{1+\sin \theta}$$​

पहले पद को तोड़ते हैं:$$\frac{1}{\cos \theta}+\frac{\sin \theta}{\cos \theta}+\frac{\cos \theta}{1+\sin \theta}$$$$= \sec \theta+\tan \theta+\frac{\cos \theta}{1+\sin \theta}$$​

अब अंतिम पद को सरल करें:
हर और हर में $1-\sin \theta$ से गुणा करें:$$\frac{\cos \theta}{1+\sin \theta}\times\frac{1-\sin \theta}{1-\sin \theta}$$$$= \frac{\cos \theta(1-\sin \theta)}{1-\sin^2\theta}$$$$= \frac{\cos \theta(1-\sin \theta)}{\cos^2\theta}$$$$= \frac{1-\sin \theta}{\cos \theta}$$$$= \sec \theta-\tan \theta$$

अब जोड़ते हैं:

$$\sec \theta+\tan \theta+\sec \theta-\tan \theta$$$$=2\sec \theta$$

(d) निम्न बारंबारता बंटन से माध्यक ज्ञात कीजिए :

Ans. चरण 1: कुल बारंबारता (N)

$$N = 6+9+20+15+9 = 59$$$$\frac{N}{2} = \frac{59}{2} = 29.5$$

चरण 2: संचयी बारंबारता (C.F.)

29.5 20–30 वर्ग में आता है

चरण 3: माध्यक का सूत्र

$$\text{माध्यक} = l + \left(\frac{\frac{N}{2}-cf}{f}\right)h$$

जहाँ,
$l = 20$ (माध्यक वर्ग की निम्न सीमा)
$cf = 15$(माध्यक वर्ग से पहले की संचयी बारंबारता)
$f = 20$
$h = 10$

मान रखने पर:

$$\text{माध्यक} = 20 + \left(\frac{29.5-15}{20}\right)\times 10$$ $$= 20 + \frac{14.5}{20}\times 10$$$$= 20 + 7.25$$ $$= 27.25$$

(e) संख्याओं 92 और 510 का LCM ज्ञात कीजिए।
Ans. दिया है:
संख्याएँ 92 और 510

चरण 1: अभाज्य गुणनखंड करें

$$92 = 2 \times 2 \times 23 = 2^2 \times 23$$$$510 = 2 \times 3 \times 5 \times 17$$

चरण 2: LCM के लिए सभी अभाज्य गुणकों की उच्चतम घात लें

$$\text{LCM} = 2^2 \times 3 \times 5 \times 17 \times 23$$

चरण 3: गुणा करें

$$2^2 = 4$$ $$4 \times 3 = 12$$$$12 \times 5 = 60$$$$60 \times 17 = 1020$$ $$1020 \times 23 = 23460$$

अन्तिम उत्तर:

$$\boxed{\text{LCM}(92,\;510)=23460}$$

(d) सिद्ध कीजिए कि √3 एक अपरिमेय संख्या है।
Ans. विरोधाभास विधि से सिद्धि:

मान लीजिए कि √3 एक परिमेय संख्या है।
तब इसे दो सहाभाज्य पूर्णांकों के अनुपात में लिखा जा सकता है:$$\sqrt{3}=\frac{p}{q}$$

जहाँ $p$ और $q$ सहाभाज्य पूर्णांक हैं तथा $q\neq 0$

दोनों पक्षों का वर्ग करें:$$3=\frac{p^2}{q^2}$$ $$p^2=3q^2$$

इससे स्पष्ट है कि $p^2$ 3 से विभाज्य है ⇒ $p$ भी 3 से विभाज्य होगा।
मान लें $p=3k$

अब मान रखें:$$(3k)^2=3q^2$$ $$9k^2=3q^2$$ $$q^2=3k^2$$

अतः $q^2$ भी 3 से विभाज्य है ⇒ $q$ भी 3 से विभाज्य होगा।

विरोधाभास:

यह पाया कि $p$ और $q$दोनों 3 से विभाज्य हैं,
जबकि प्रारम्भ में माना था कि वे सहाभाज्य हैं।

यह विरोधाभास है।

अतः निष्कर्ष:

हमारी प्रारम्भिक धारणा गलत है।
इसलिए,$$\boxed{\sqrt{3}\ \text{एक अपरिमेय संख्या है।}}$$​

2. किन्ही पाँच खण्डों को हल कीजिए:

(a) निम्नलिखित सारिणी से बहुलक ज्ञात कीजिए:

Ans. चरण 1: बहुलक वर्ग (Modal Class)

सबसे अधिक बारंबारता 23 है
👉 बहुलक वर्ग = 30–40

चरण 2: बहुलक का सूत्र

$$\text{बहुलक} = l + \left(\frac{f_1 – f_0}{2f_1 – f_0 – f_2}\right)h$$

जहाँ,
$l = 30$ (बहुलक वर्ग की निम्न सीमा)
$f_1 = 23$ (बहुलक वर्ग की बारंबारता)
$f_0 = 21$ (पूर्ववर्ती वर्ग की बारंबारता)
$f_2 = 14$ (अनुवर्ती वर्ग की बारंबारता)
$h = 10$

चरण 3: मान रखने पर

$$\text{बहुलक} = 30 + \left(\frac{23-21}{2(23)-21-14}\right)\times 10$$ $$= 30 + \left(\frac{2}{46-35}\right)\times 10$$$$= 30 + \frac{2}{11}\times 10$$$$= 30 + 1.82$$ $$= 31.82$$

अन्तिम उत्तर:

$$\boxed{\text{बहुलक} \approx 31.82}$$​

(b) सिद्ध कीजिए कि किसी बाह्य बिन्दु से वृत्त पर खींची गई स्पर्श रेखाओं की लम्बाइयाँ बराबर होती हैं।
Ans. मान लीजिए O केन्द्र वाला एक वृत्त है और P कोई बाह्य बिन्दु है।
बिन्दु P से वृत्त पर दो स्पर्श रेखाएँ PA तथा PB खींची गई हैं, जो क्रमशः बिन्दुओं A और B पर वृत्त को स्पर्श करती हैं।

प्रमाण:

स्पर्श बिन्दु पर त्रिज्या स्पर्श रेखा पर लम्ब होती है, अतः$$OA \perp PA \quad \text{और} \quad OB \perp PB$$

अब, त्रिभुज ΔOPA और ΔOPB पर विचार करें:

1. $OA = OB$ (एक ही वृत्त की त्रिज्याएँ)
2. $\angle OAP = \angle OBP = 90^\circ$
3. $OP = OP$ (सामान्य भुजा)

अतः,$$\triangle OPA \cong \triangle OPB \quad (\text{RHS सर्वांगसमता})$$

निष्कर्ष:

सर्वांगसम त्रिभुजों की संगत भुजाएँ बराबर होती हैं, इसलिए$$PA = PB$$

अतः सिद्ध हुआ कि किसी बाह्य बिन्दु से वृत्त पर खींची गई स्पर्श रेखाओं की लम्बाइयाँ बराबर होती हैं।

(c) एक त्रिभुज ABC की भुजा BC पर एक बिन्दु D इस प्रकार स्थित है कि ∠ADC = ∠BAC है। सिद्ध कीजिए कि CA²= CB. CD है।
Ans. दिया हुआ:

त्रिभुज $ABC$ में $BC$ पर बिन्दु $D$ ऐसा है कि
$\angle ADC = \angle BAC$

प्रमाण:

त्रिभुज $\triangle ADC$ और $\triangle BAC$ पर विचार करें।

दिया है:$$\angle ADC = \angle BAC \quad \text{(दिया हुआ)}$$

साथ ही,$$\angle ACD = \angle BCA \quad \text{(सामान्य कोण)}$$

अतः,$$\triangle ADC \sim \triangle BAC \quad \text{(AA समानता)}$$

समान त्रिभुजों में संगत भुजाओं का अनुपात बराबर होता है:

$$\frac{CA}{CB} = \frac{CD}{CA}$$

क्रॉस गुणा करने पर:$$CA \times CA = CB \times CD$$$$CA^2 = CB \cdot CD$$

अतः सिद्ध हुआ कि

$$\boxed{CA^2 = CB \cdot CD}$$

(d) दो अंकों की एक संख्या के अंकों का योग 9 है। इस संख्या का 9 गुना संख्या के अंकों को पलटने से बनी संख्या का 2 गुना है। वह संख्या ज्ञात कीजिए।
Ans. मान लीजिए दो अंकों की संख्या 10x+y है,
जहाँ
$x$= दहाई का अंक,
$y$ = इकाई का अंक।

दिया है:

1. अंकों का योग = 9

$$x + y = 9 \quad \text{…(1)}$$

2. संख्या का 9 गुना = अंकों को पलटने से बनी संख्या का 2 गुना

अंकों को पलटने से बनी संख्या = $10y + x$$$9(10x + y) = 2(10y + x)$$$$90x + 9y = 20y + 2x$$ $$90x – 2x = 20y – 9y$$ $$88x = 11y$$$$y = 8x \quad \text{…(2)}$$

(1) और (2) से:

$$x + 8x = 9$$$$9x = 9$$ $$x = 1$$ $$y = 8$$

संख्या =

$$10x + y = 10(1) + 8 = 18$$

अन्तिम उत्तर:

$$\boxed{18}$$​

(e) द्विघात समीकरण 2x²-5x+3=0 को हल कीजिए।
Ans. चरण 1: गुणनखंड विधि से हल करें

$$2x^2 – 5x + 3 = 0$$

मध्य पद को विभाजित करें:$$2x^2 – 2x – 3x + 3 = 0$$ $$2x(x-1) -3(x-1)=0$$$$(x-1)(2x-3)=0$$

चरण 2: प्रत्येक गुणनखंड को शून्य के बराबर रखें

1. $x – 1 = 0 \Rightarrow x = 1$
2. $2x – 3 = 0 \Rightarrow x = \frac{3}{2}$

अन्तिम उत्तर:

$$\boxed{x = 1 \quad \text{या} \quad x = \frac{3}{2}}$$

(f) यदि एक बगीचे की परिमाप 120 मी और क्षेत्रफल 800 मी² है, तो उसकी लम्बाई और चौड़ाई ज्ञात कीजिए। दिया है कि लम्बाई, चौड़ाई से 2 गुनी है।
Ans. दिया है:

परिमाप $=120$ मी
क्षेत्रफल $=800$ मी²

चरण 1: परिमाप का सूत्र

$$2(l+b)=120$$ $$2(2x+x)=120$$ $$2(3x)=120$$ $$6x=120 \Rightarrow x=20$$

चौड़ाई = 20 मी,
लम्बाई = 2x = 40 मी

चरण 2: क्षेत्रफल से जाँच

$$\text{क्षेत्रफल} = l \times b = 40 \times 20 = 800 \text{ मी}^2$$

(दिया हुआ क्षेत्रफल सही मिलता है)

अन्तिम उत्तर:

$$\boxed{\text{लम्बाई} = 40 \text{ मी}, \quad \text{चौड़ाई} = 20 \text{ मी}}$$

3. निम्नलिखित समीकरणों को हल कीजिए: (3/2) x – (5/3) y = – 2, x/3 + y/2 = 13/6
Ans. दिए गए रैखिक समीकरण हैं:$$\frac{3}{2}x – \frac{5}{3}y = -2 \quad \text{…(1)}$$$$\frac{x}{3} + \frac{y}{2} = \frac{13}{6} \quad \text{…(2)}$$

चरण 1: भिन्न हटाएँ

समीकरण (1) को 6 से गुणा करें:$$9x – 10y = -12 \quad \text{…(3)}$$

समीकरण (2) को 6 से गुणा करें:$$2x + 3y = 13 \quad \text{…(4)}$$

चरण 2: उन्मूलन विधि

समीकरण (3):$$9x – 10y = -12$$

समीकरण (4) को 5 से गुणा करें:$$10x + 15y = 65 \quad \text{…(5)}$$

अब (5) और (3) जोड़ें:$$(9x – 10y) + (10x + 15y) = -12 + 65$$ $$19x + 5y = 53 \quad \text{…(6)}$$

चरण 3: y का मान निकालें

समीकरण (4) से:$$2x + 3y = 13$$

$x$ का मान (6) से लें:$$19x + 5y = 53$$

इन दोनों को हल करने पर:$$x = 4$$

चरण 4: x=4 को (4) में रखें

$$2(4) + 3y = 13$$$$8 + 3y = 13$$$$3y = 5 \Rightarrow y = 3$$

अन्तिम उत्तर:

$$\boxed{x = 4,\; y = 3}$$

अथवा

उस A.P. के प्रथम 51 पदों का योग ज्ञात कीजिए जिसके दूसरे और तीसरे पद क्रमशः 14 और 18 हैं।
Ans. दिया है कि एक समान्तर श्रेणी (A.P.) के

दूसरा पद $a_2 = 14$
तीसरा पद $a_3 = 18$

चरण 1: प्रथम पद और अंतर ज्ञात करें

A.P. में$$a_2 = a + d = 14 \quad \text{…(1)}$$$$a_3 = a + 2d = 18 \quad \text{…(2)}$$

(2) − (1):$$(a+2d) – (a+d) = 18 – 14$$ $$d = 4$$

अब (1) में $d = 4$ रखें:$$a + 4 = 14 \Rightarrow a = 10$$

चरण 2: प्रथम 51 पदों का योग

सूत्र:$$S_n = \frac{n}{2}\,[2a + (n-1)d]$$

यहाँ
$n = 51,\; a = 10,\; d = 4$$$S_{51} = \frac{51}{2}[2(10) + 50 \times 4]$$$$= \frac{51}{2}[20 + 200]$$$$= \frac{51}{2} \times 220$$$$= 51 \times 110$$ $$= 5610$$

अन्तिम उत्तर:

$$\boxed{S_{51} = 5610}$$

4. एक मीनार के ऊपर एक झंडा लगा है। मीनार के आधार से 10 मी की दूरी पर मीनार तथा झंडे के शिखर के उन्नयन कोण क्रमशः 45° और 60° हैं। झंडे की लम्बाई ज्ञात कीजिए।
Ans. दिया है:
मीनार के आधार से बिन्दु की दूरी = 10 मी

मीनार के शीर्ष का उन्नयन कोण = 45°
झंडे के शीर्ष का उन्नयन कोण = 60°

मान लें,
मीनार की ऊँचाई = $h$ मी
झंडे की लम्बाई = $x$ मी

चरण 1: मीनार की ऊँचाई ज्ञात करें

$$\tan 45^\circ = \frac{h}{10}$$​ $$1 = \frac{h}{10} \Rightarrow h = 10 \text{ मी}$$

चरण 2: मीनार + झंडे की कुल ऊँचाई

$$\tan 60^\circ = \frac{h + x}{10}$$​ $$\sqrt{3} = \frac{10 + x}{10}$$$$10\sqrt{3} = 10 + x$$ $$x = 10\sqrt{3} – 10$$

अन्तिम उत्तर:

$$\boxed{\text{झंडे की लम्बाई} = 10(\sqrt{3}-1)\ \text{मीटर}}$$

(लगभग $= 7.32$=7.32 मी)

अथवा

50 मी ऊँची मीनार की चोटी से एक खंभे के ऊपरी सिरे और आधार के अवनमन कोण क्रमशः 45° और 60° हैं। खंभे की ऊँचाई ज्ञात कीजिए।
Ans. दिया है:
मीनार की ऊँचाई = 50 मी

मीनार की चोटी से

• खंभे के आधार का अवनमन कोण = 60°
• खंभे के ऊपरी सिरे का अवनमन कोण = 45°

मान लें,
मीनार के पाद से खंभे के पाद तक क्षैतिज दूरी = x मी
खंभे की ऊँचाई = h मी

(अवनमन कोण = उन्नयन कोण)

चरण 1: खंभे के आधार के लिए

$$\tan 60^\circ = \frac{50}{x}$$$$\sqrt{3} = \frac{50}{x} \Rightarrow x = \frac{50}{\sqrt{3}}$$

चरण 2: खंभे के शीर्ष के लिए

ऊँचाई का अंतर = $50 – h$$$\tan 45^\circ = \frac{50-h}{x}$$ $$1 = \frac{50-h}{50/\sqrt{3}}$$​ $$50 – h = \frac{50}{\sqrt{3}}$$ $$h = 50 – \frac{50}{\sqrt{3}}$$

अन्तिम रूप में

$$h = \frac{50(\sqrt{3}-1)}{\sqrt{3}}$$​

या परिमेयक करने पर,$$h = \frac{50(3-\sqrt{3})}{3}$$

अन्तिम उत्तर:

$$\boxed{\text{खंभे की ऊँचाई } = \frac{50(3-\sqrt{3})}{3}\ \text{मीटर}}$$

(लगभग 21.1 मी)

5. 15 सेमी त्रिज्या वाले वृत्त की कोई जीवा केन्द्र पर 60° का कोण अन्तरित करती है। लघु और दीर्घ वृत्तखंडों के क्षेत्रफल ज्ञात कीजिए। ( π = 3.14, √3 =1.73)
Ans. दिया है:
वृत्त की त्रिज्या $r = 15$
केन्द्र पर कोण $\theta = 60^\circ$
$\pi = 3.14,\; \sqrt{3} = 1.73$

चरण 1: सेक्टर (60°) का क्षेत्रफल

$$\text{सेक्टर का क्षेत्रफल}=\frac{\theta}{360^\circ}\,\pi r^2 =\frac{60}{360}\times 3.14 \times 15^2$$$$=\frac{1}{6}\times 3.14 \times 225 =\frac{706.5}{6} =117.75\ \text{सेमी}^2$$

चरण 2: त्रिभुज का क्षेत्रफल

केन्द्र पर बना त्रिभुज समद्विबाहु है;$$\text{त्रिभुज का क्षेत्रफल}=\frac{1}{2}r^2\sin 60^\circ =\frac{1}{2}\times 225 \times \frac{\sqrt{3}}{2}$$ $$=112.5 \times 0.865 \approx 97.31\ \text{सेमी}^2$$

चरण 3: लघु वृत्तखंड का क्षेत्रफल

$$\text{लघु वृत्तखंड}=\text{सेक्टर} – \text{त्रिभुज} =117.75-97.31 =20.44\ \text{सेमी}^2$$

चरण 4: दीर्घ वृत्तखंड का क्षेत्रफल

पूरे वृत्त का क्षेत्रफल:$$\pi r^2=3.14\times 225=706.5\ \text{सेमी}^2$$ $$\text{दीर्घ वृत्तखंड}=706.5-20.44 =686.06\ \text{सेमी}^2$$

अथवा

लकड़ी के एक ठोस बेलन के प्रत्येक सिरे पर एक अर्द्धगोला निकालकर एक वस्तु बनायी गयी है। यदि बेलन की ऊँचाई 10 सेमी और आधार की त्रिज्या 3.5 सेमी हैं, तो इस वस्तु का सम्पूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
Ans. दिया है:
बेलन की ऊँचाई $h = 10$ सेमी
आधार की त्रिज्या $r = 3.5$ सेमी

बेलन के दोनों सिरों से अर्द्धगोले निकाल दिए गए हैं,
अतः समतल वृत्तीय सतहें नहीं रहेंगी।

इस वस्तु का सम्पूर्ण पृष्ठीय क्षेत्रफल =

$$\text{बेलन का वक्र पृष्ठीय क्षेत्रफल} + \text{दो अर्द्धगोलों का वक्र पृष्ठीय क्षेत्रफल}$$

1️⃣ बेलन का वक्र पृष्ठीय क्षेत्रफल

$$= 2\pi rh$$$$= 2 \times \frac{22}{7} \times 3.5 \times 10$$ $$= 220\ \text{सेमी}^2$$

2️⃣ दो अर्द्धगोलों का वक्र पृष्ठीय क्षेत्रफल

(दो अर्द्धगोले = एक गोला)$$= 4\pi r^2$$$$= 4 \times \frac{22}{7} \times (3.5)^2$$$$= 4 \times \frac{22}{7} \times 12.25$$$$= 154\ \text{सेमी}^2$$

3️⃣ सम्पूर्ण पृष्ठीय क्षेत्रफल

$$= 220 + 154 = 374\ \text{सेमी}^2$$