मशीन के प्रकार (Types of Machines)

इस लेख में हम मशीन के प्रकार (Types of Machines) के बारे में विस्तार से जानकारी प्राप्त करेंगे। तो आइए निम्नलिखित परिभाषाओं को पढ़ते हैं –

(1) उत्तोलक (Lever)

उत्तोलक या लीवर वह सरल मशीन है जो किसी बिंदु (आलंब/Fulcrum) के चारों ओर घूमकर बल की सहायता से भारी वस्तु को उठाने या किसी कार्य को सरल बनाने के लिए उपयोग की जाती है। इसके निम्नलिखित बिन्दु होते हैं –

(a) आलंब (Fulcrum) – छड़ जिस स्थिर (fix) बिन्दु के चारों तरफ घूम सकती है उसे आलंब कहते हैं।

(b) आयास (Effort) – उत्तोलक को उपयोग में लाने के लिए उस पर जो बल लगाया जाता है, उसे आयास कहते हैं।

(c) भार (Load) – उत्तोलक द्वारा उठाया गया बोझ या किया गया कार्य, भार कहलाता है।

• उत्तोलक का सिद्धान्त (Principle of Lever)

आयास आयास भुजा = भार भार भुजा (Effort Effort Arm = Load × Load Arm.)

• मशीन या उत्तोलक का यांत्रिक लाभ (Mechanical Advantage of Lever)

उत्तोलक द्वारा उठाए गए भार और उस पर लगाई गई बल (Effort) के अनुपात को यांत्रिक लाभ (Mechanical Advantage, MA) कहते हैं।$$\text{यांत्रिक लाभ (MA)} = \frac{\text{उठाया गया भार (Load)}}{\text{लगाया गया बल (Effort)}}$$

विशेषता:

• यांत्रिक लाभ जितना अधिक होगा, उतना ही कम बल लगाकर भारी वस्तु उठाई जा सकती है।
• यह उत्तोलक की दक्षता को बताता है।

उदाहरण:
यदि किसी उत्तोलक पर 100 N का भार 20 N बल से उठाया जा रहा है, तो$$MA = \frac{100}{20} = 5$$

इसका अर्थ है कि उत्तोलक 5 गुना बल बढ़ाता है।

• मशीन का वेग अनुपात (Velocity Ratio of Machine)

1. वेग अनुपात (VR):$$\text{VR} = \frac{\text{Effort बिंदु द्वारा चली गई दूरी}}{\text{Load बिंदु द्वारा चली गई दूरी}}$$

• इसका अर्थ है कि उत्तोलक पर प्रयुक्त बल कितनी दूरी तय करता है, बनिस्पत भार की दूरी के।
• जितनी अधिक दूरी Effort तय करता है, उतना ही कम बल भार को उठाने में लगता है।

2. घर्षण रहित उत्तोलक:

• यदि उत्तोलक पर कोई घर्षण नहीं है, तो

$$\text{यांत्रिक लाभ (MA)} = \text{वेग अनुपात (VR)}$$

• इसका मतलब है कि बल का लाभ और दूरी का अनुपात बराबर होता है।

विशेषता:

• यह आदर्श स्थिति होती है।
• वास्तविक जीवन में हमेशा थोड़ी बहुत ऊर्जा घर्षण में खो जाती है, इसलिए MA < VR होता है।

उत्तोलक के प्रकार (Types of Lever)

आलम्ब (Fulcrum or fix point), आयास (Effort) व भार (Weight of Load) की अलग-अलग स्थितियाँ संभव है। इसी आधार पर उत्तोलकों को तीन प्रकारों में बाँटा जा सकता है-

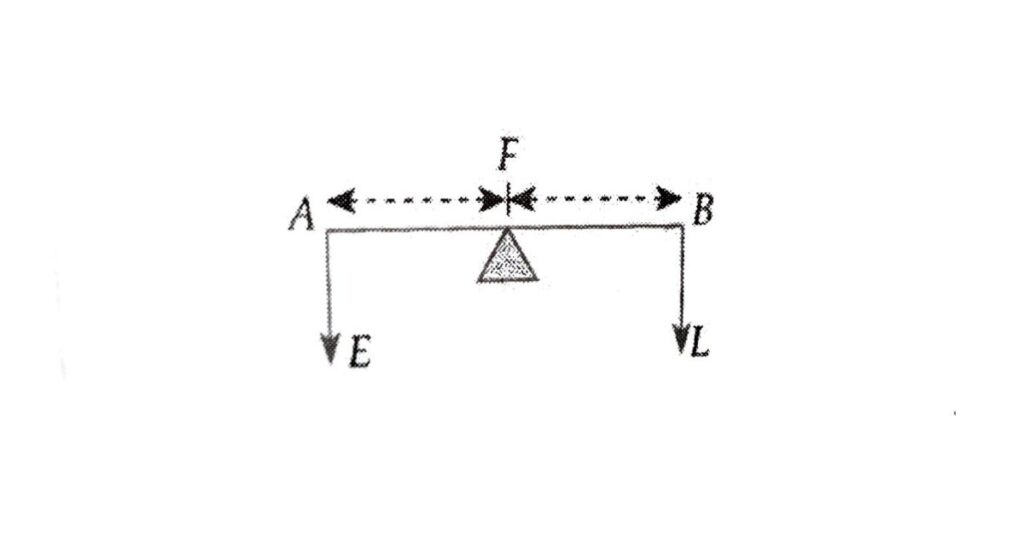
(a) प्रथम वर्ग के उत्तोलक (First class Lever)- पहली श्रेणी का उत्तोलक वह है जिसमें आलम्ब (Fulcrum) बीच में होता है और Effort और Load दोनों विपरीत दिशा में होते हैं।

विशेषताएँ:

1. बल बढ़ाने या दिशा बदलने के लिए उपयुक्त।
2. यांत्रिक लाभ (MA) कभी 1 से कम या अधिक हो सकता है, यह Effort और Load की दूरी पर निर्भर करता है।
3. घर्षण रहित उत्तोलक में MA = Velocity Ratio (VR)।

उदाहरण:

• झूला (See-saw)
• कैंची (Scissors)
• नट खोलने वाली रॉड (Nutcracker)

संतुलन में, E × PF = L × QF

उत्तोलक का यांत्रिक लाभ (MA) = Work/Effort

या M.A. =  1/E =  PF/QF = आयास भुजा/भार भुजा

इस प्रकार के उत्तोलकों में यांत्रिक लाभ 1 से अधिक, कम या बराबर कुछ भी हो सकता है। क्योंकि PF, QF से छोटा, बड़ा या बराबर भी हो सकता है।

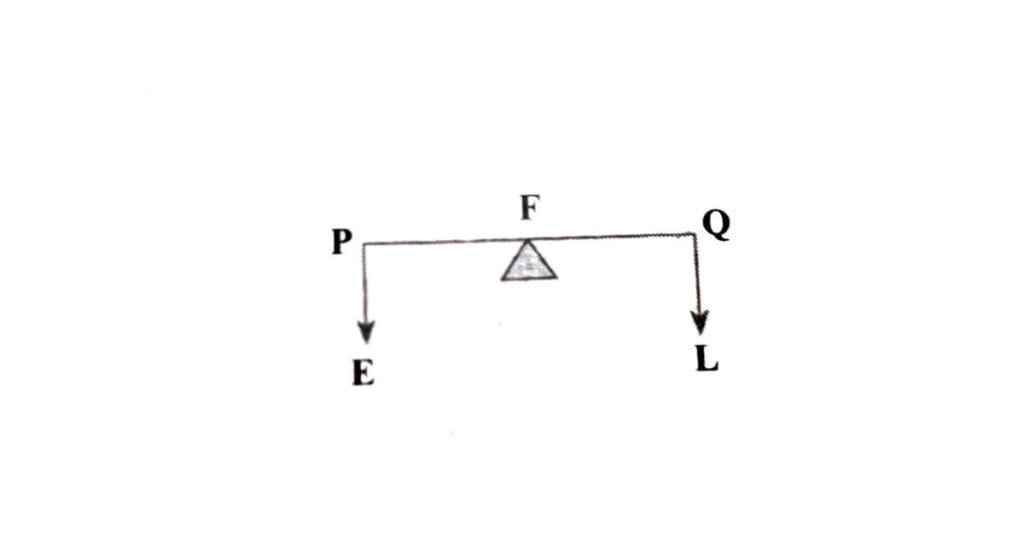
(b) द्वितीय वर्ग के उत्तोलक (Second class Lever)- दूसरी श्रेणी का उत्तोलक वह है जिसमें Load (भार) बीच में होता है, और Fulcrum (आलम्ब) तथा Effort (आयास) दोनों बाहरी छोरों पर होते हैं।

विशेषताएँ:

1. यांत्रिक लाभ (MA) हमेशा 1 से अधिक होता है।
2. बल को बढ़ाने के लिए उपयुक्त है।
3. Effort कम लगाकर भारी भार उठाया जा सकता है।

उदाहरण:

• रेहड़ी (Wheelbarrow)
• दरवाज़ा (Door)
• बेलन (Bottle Opener)

इस प्रकार के उत्तोलकों में यांत्रिक लाभ सदैव 1 से अधिक होता है। क्योंकि PF सदैव QF से बड़ा होगा। जैसे – सरौता, नीबू निचोड़ने की मशीन, एक पहिए की कूड़ा ढोने वाली गाड़ी, कब्जे पर घूमने वाला दरवाजा इत्यादि।

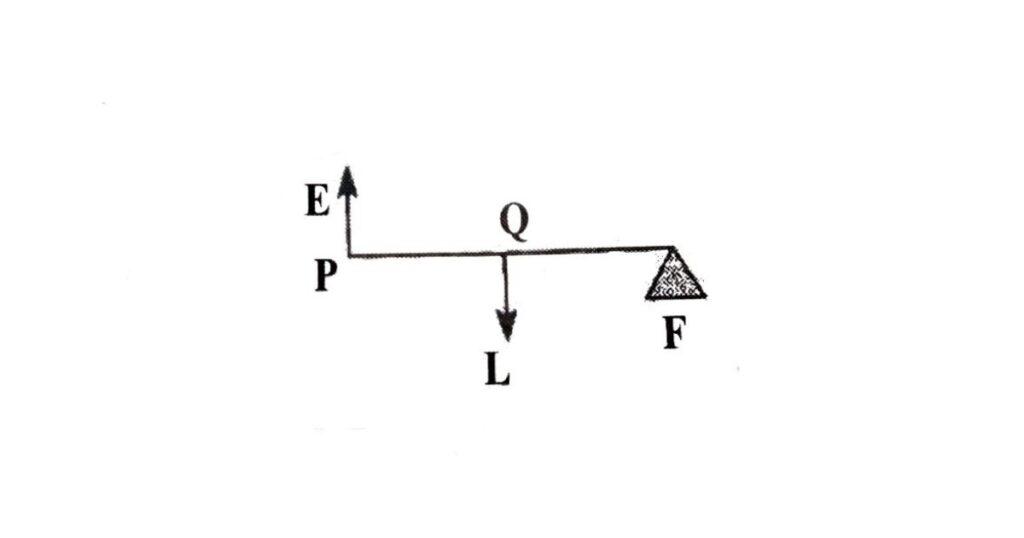
(c) तृतीय वर्ग के उत्तोलक (Third class Lever)- तृतीय श्रेणी का उत्तोलक वह है जिसमें Effort (आयास) बीच में होता है, और Fulcrum (आलम्ब) तथा Load (भार) दोनों बाहरी छोरों पर होते हैं।

विशेषताएँ:

1. बल को बढ़ाने के बजाय दूरी और गति बढ़ाने के लिए उपयुक्त।
2. यांत्रिक लाभ (MA) हमेशा 1 से कम होता है।
3. Effort अधिक लगाकर Load को हल्का उठाया जाता है।

उदाहरण:

• छड़ी से हिट करना (Bat)
• हाथ की कलाई (Forearm)
• छुरी से काटना (Knife)

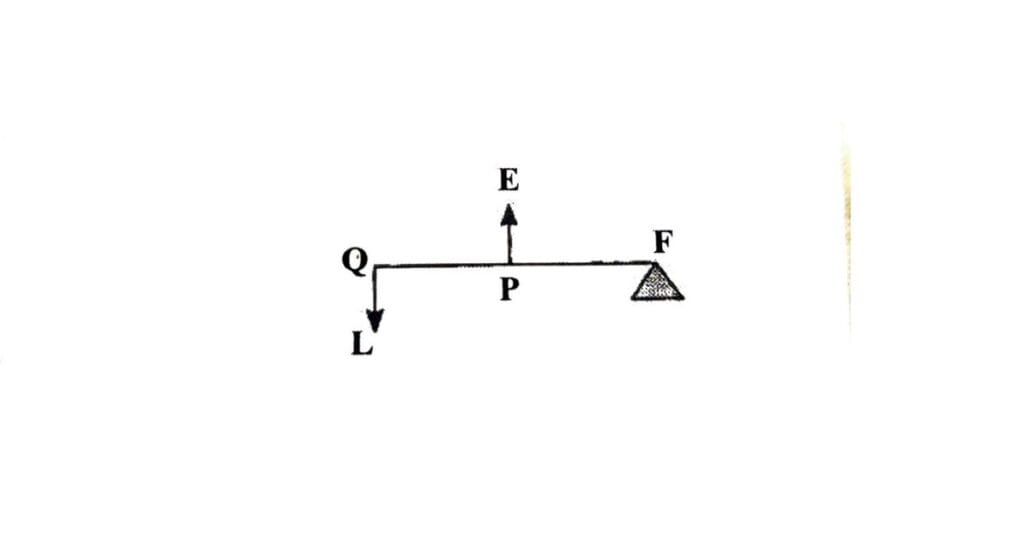
इसमें यांत्रिक लाभ सदैव 1 से कम होता है क्योंकि PF (आयास भुजा) का मान QF (भार भुजा) में सदैव कम होता है। इसके उदाहरण – चिमटा (Tongs), खेत जोतने का हल, मनुष्य का हाथ इत्यादि हैं।

(2) चक्र तथा धुरी (Wheel and Axle)

यह युक्ति भारी वस्तु को सुविधाजनक दिशा और स्थान पर बल लगाकर उठाने के लिए प्रयोग की जाती है, जैसे कुएँ से पानी खींचना। इसमें दो बेलन (Cylinder) होते हैं जिनका अक्ष (Axis) समान होता है। बड़ा बेलन जिसकी त्रिज्या अधिक और लंबाई कम होती है, उसे चक्र (Wheel) कहते हैं, और छोटा बेलन जिसकी त्रिज्या कम और लंबाई अधिक होती है, उसे धुरी (Axle) कहते हैं।

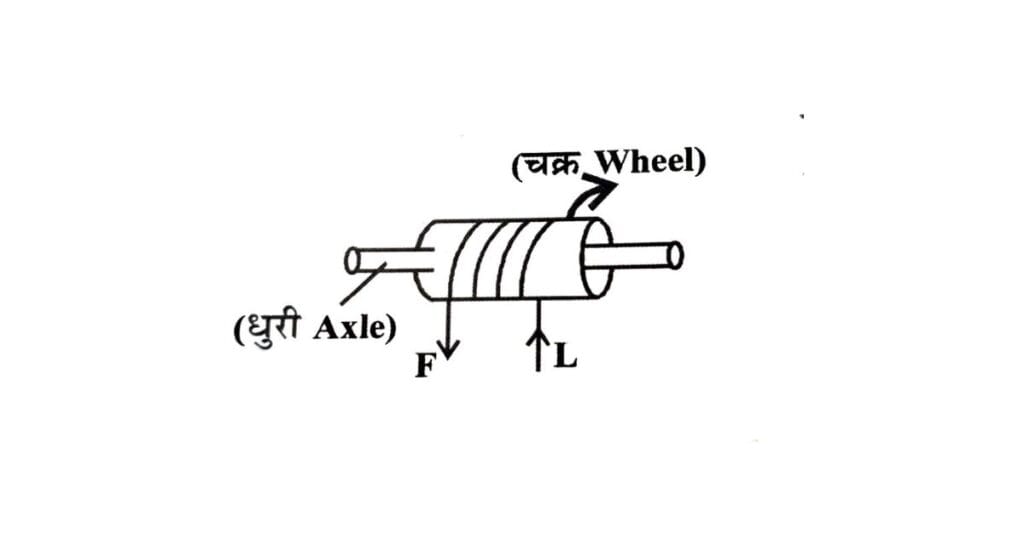
चक्र पर रस्सी लिपटी होती है जिस पर एक तरफ भार (Load) लटका या बंधा (tied) होता है व दूसरी तरफ बल लगाया जाता है।

इसका यांत्रिक लाभ निम्न सूत्र से निकाला जाता है-

यांत्रिक लाभ = चक्र की त्रिज्या (R)/धुरी की त्रिज्या (r) = वेग अनुपात

चूँकि R > r, अतः इसका यांत्रिक लाभ सदैव 1 से अधिक होता है।

(3) घिरनियाँ (Pulleys)

यह युक्ति चक्र और धुरी से मिलती-जुलती है, लेकिन इसमें एक से अधिक घिरनियाँ जुड़ी होती हैं। इनका संयोजन इस प्रकार किया जाता है कि बल लगाने की दिशा और स्थान सुविधाजनक हो, जिससे कम Effort लगाकर अधिक भारी वस्तु उठाई जा सके।

(4) स्क्रू जैक (Screw Jack)

यह युक्ति भारी वाहनों जैसे कार, ट्रक, बस आदि को नीचे से ऊपर उठाने के लिए प्रयोग की जाती है, ताकि उनकी सफाई की जा सके या टायर व ट्यूब बदला जा सके। इसमें एक चूड़ी-कटा बेलन होता है, जिसके अंदर एक खोखला बेलन फिट किया जाता है, जो ऊपर-नीचे चलता है। जिस वस्तु को उठाना होता है, उसके नीचे बेलन लगाया जाता है और रॉड की सहायता से घुमाकर ऊपर उठाया जाता है, जिससे वस्तु भी ऊपर उठ जाती है।

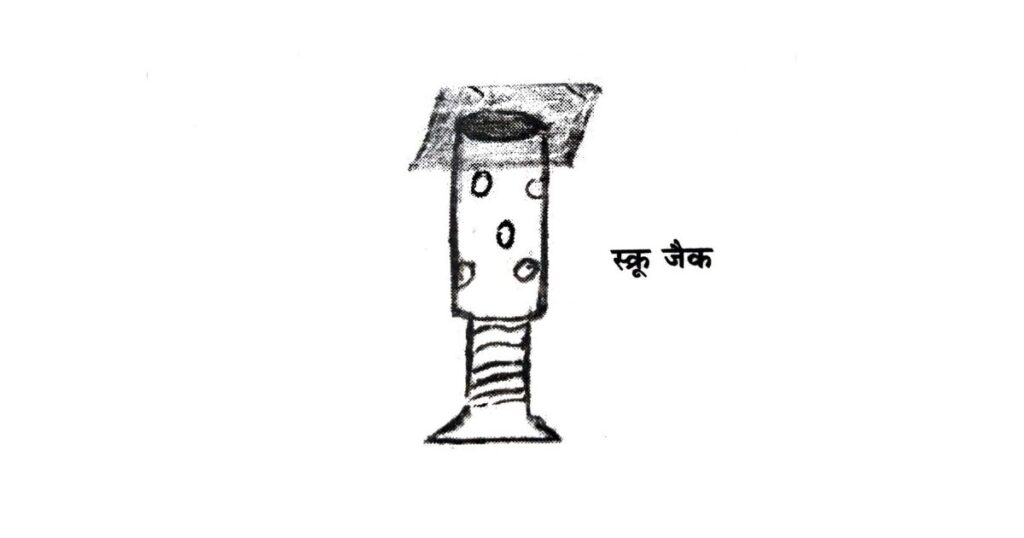
(5) आनत तल (Inclined plane)

जब कोई तल (Plane or Surface) किसी कोण पर झुका होता है, तो उसे आनत तल (Inclined Plane) कहते हैं। इसका प्रयोग भारी सामानों को ऊँचाई तक पहुँचाने में किया जाता है, जैसे ट्रक में सामान लादना। आनत तल का लाभ यह है कि सीधे ऊर्ध्वाधर उठाने की तुलना में भार को खींचना आसान हो जाता है, क्योंकि भार दो दिशाओं में वितरित हो जाता है और कम बल (Effort) से काम पूरा किया जा सकता है।

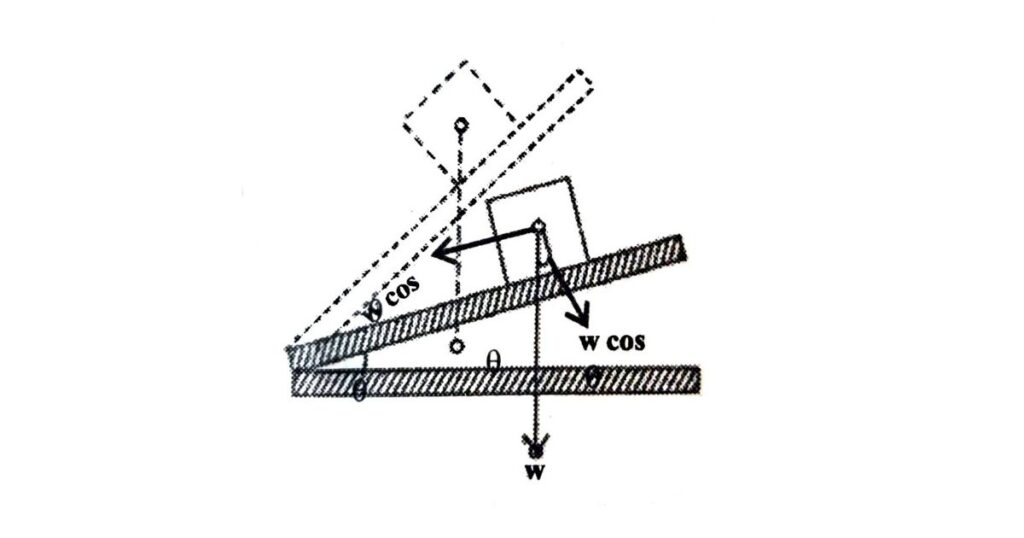
आनत तल के लम्बवत् नीचे की ओर = w cosθ व, आनत तल के समानान्तर नीचे की ओर = w sinθ इस प्रकार वस्तु का प्रभावी भार w sine ही रह जाता है जो कि W से कम होता है।

आनत तल का यांत्रिक लाभ (MA) = आनत तल की लंबाई/आनत तल की ऊँचाई or, Length of inclined plane/Height of inclined plane

गियर (Gear)

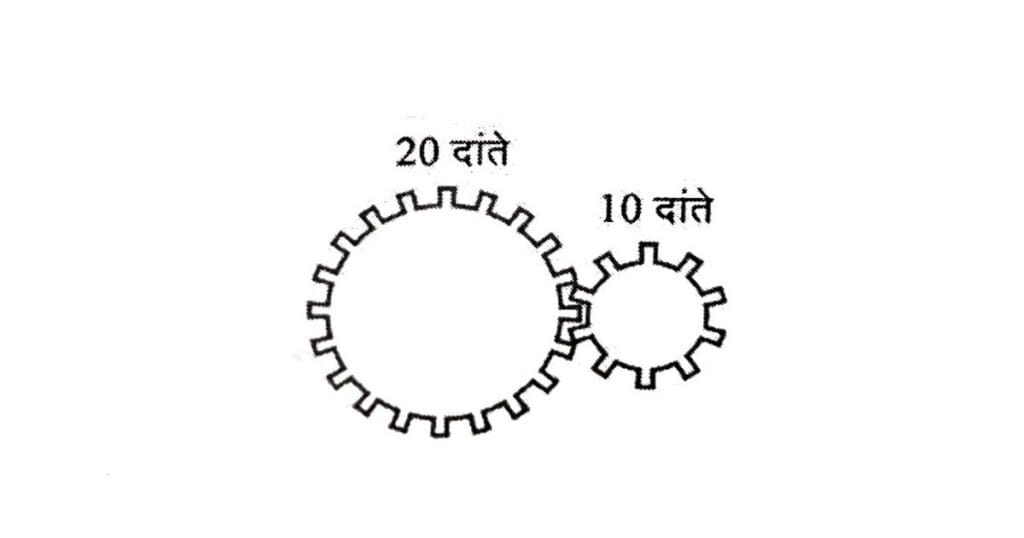
दाँतेदार पुल्लियों (Toothed Pulleys) के संयोजन को गियर (Gear) कहते हैं। इसका प्रयोग यंत्रों में यांत्रिक लाभ (Mechanical Advantage) बढ़ाने या घटाने और पुल्लियों के वेग अनुपात (Speed Ratio) बदलने के लिए किया जाता है। उदाहरण के लिए, यदि 100 दाँतों वाली गियरपुल्ली का एक चक्कर घूमें, तो 25 दाँतों वाली गियरपुल्ली चार चक्कर घूमेगी, जिससे छोटी पुल्ली की घूर्णन गति बड़ी पुल्ली से चार गुनी हो जाती है। अतः

वेग अनुपात= बड़े पुली में दाँतों की संख्या/छोटे पुली में दाँतों की संख्या

गुरुत्व केंद्र (Centre of Gravity)

किसी वस्तु का गुरुत्व केंद्र वह बिंदु होता है जहाँ वस्तु का समस्त भार केंद्रित होता है, चाहे वस्तु किसी भी स्थिति में रखी जाए।

व्याख्या:

• प्रत्येक वस्तु असंख्य अणुओं (molecules) से बनी होती है।
• प्रत्येक अणु पर पृथ्वी द्वारा आकर्षण (Gravity) कार्य करता है, जिससे प्रत्येक कण वस्तु पर नीचे की दिशा में बल लगाता है।
• ये बल लगभग समानांतर माने जा सकते हैं क्योंकि पृथ्वी का गुरुत्व केंद्र वस्तु से बहुत दूर होता है।
• वस्तु पर लगने वाले ये सभी बल पिण्ड को घुमाने का प्रयास करते हैं, लेकिन जब वस्तु संतुलन (Equilibrium) में होती है, तो किसी भी बिंदु के सापेक्ष सभी बलों का घूर्णन योग शून्य हो जाता है।
• इस प्रकार, गुरुत्व केंद्र वह बिंदु है जहाँ सभी बलों का परिणामी बल सीधे नीचे कार्य करता है और यह बल वस्तु के भार के बराबर होता है।
• यदि इस बिंदु पर बराबर और विपरीत दिशा में बल लगाया जाए, तो वस्तु संतुलित रहती है।

यह सरल भाषा में कहें तो, गुरुत्व केंद्र वह बिंदु है जहाँ से वस्तु का वजन पूरी तरह लग रहा हो और इसे उसी बिंदु पर सहारा देकर वस्तु को संतुलित रखा जा सकता है।

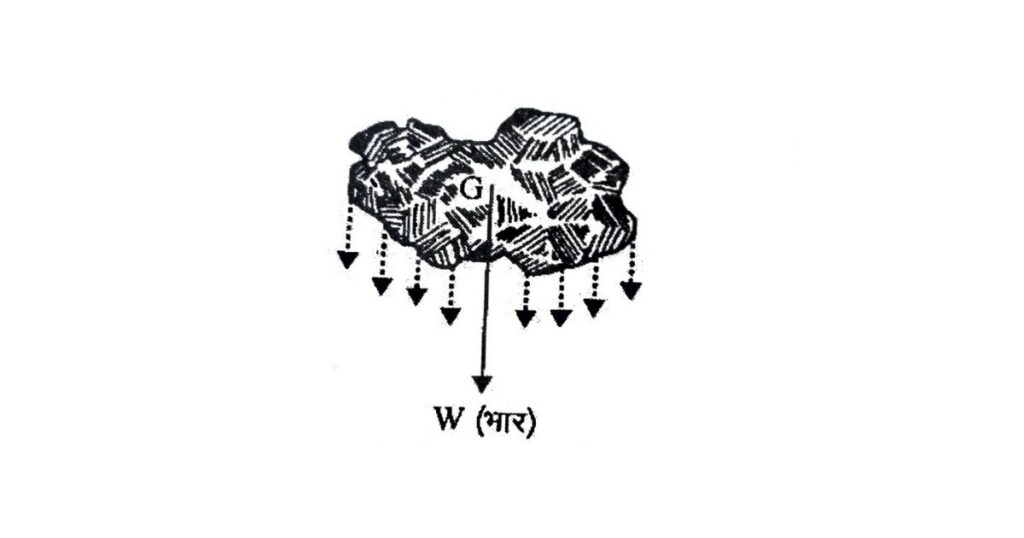
गुरुत्व केंद्र के आधार पर संतुलन की व्याख्या

स्थायी संतुलन (Stable Equilibrium)

यदि किसी संतुलित पिण्ड को थोड़ा सा विस्थापित किया जाए और उसके गुरुत्व केंद्र के ठीक नीचे कार्यकारी बल की रेखा अब भी उसके आधार से होकर गुजरती है, तो विस्थापन हटाने पर पिण्ड अपनी पूर्वावस्था में वापस आ जाता है। यह अधिक संभावना तब होती है जब पिण्ड का आधार व्यापक, भारी, या दोनों हो। ऐसी वस्तुओं का गुरुत्व केंद्र आधार के समीप होता है, जिससे उनका भार आधार से होकर गुजरता है और पिण्ड अपने आप संतुलित रहता है। सरल शब्दों में, स्थायी संतुलन वाली वस्तुएँ थोड़ा सा हिलने पर भी अपनी मूल स्थिति में लौट आती हैं।

अस्थायी संतुलन (Unstable Equilibrium)

यदि किसी वस्तु का आकार या स्थिति ऐसी हो कि संतुलनावस्था से थोड़ा सा विस्थापन होने पर उसके भार की क्रिया रेखा आधार से बाहर चली जाती है, तो वस्तु पूर्वावस्था में वापस नहीं आती। इसे अस्थायी संतुलन कहते हैं। उदाहरण के लिए, सीधे रखे ठोस शंकु का संतुलन स्थायी होता है, जबकि उल्टा रखा शंकु या पतली लंबी छड़ अस्थायी संतुलन में होती है। सरल शब्दों में, अस्थायी संतुलन वाली वस्तुएँ थोड़ा सा हिलने पर अपने आप संतुलित नहीं होतीं।

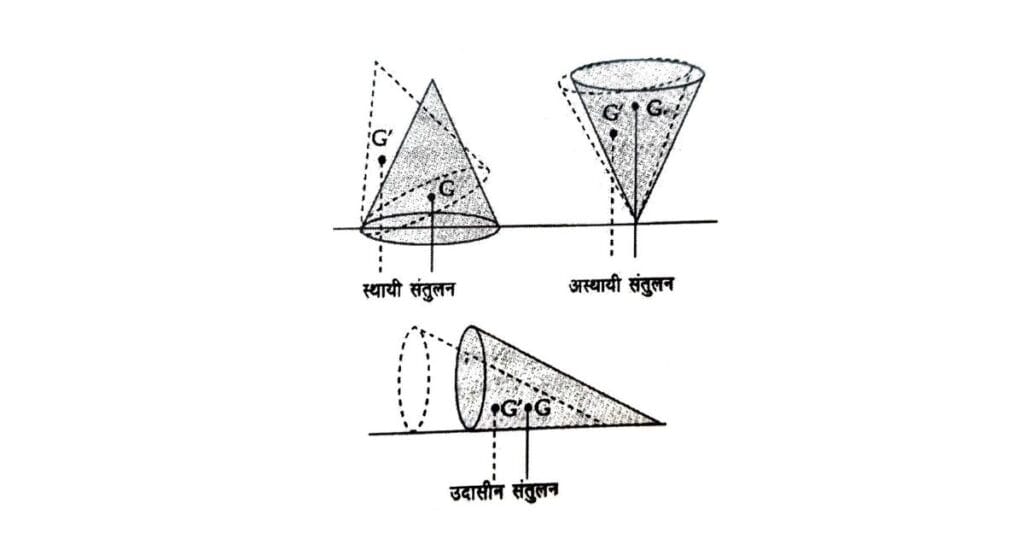
उदासीन संतुलन (Neutral Equilibrium)

ऐसी वस्तुएँ जिनके भार की क्रिया रेखा संतुलनावस्था से थोड़ा सा विस्थापन होने पर नए आधार से होकर गुजरने लगती हैं, वे न तो वापस अपनी पूर्वावस्था में लौटती हैं और न ही असंतुलित होती हैं। इस प्रकार का संतुलन उदासीन संतुलन कहलाता है। उदाहरण के लिए, समतल पर पड़ा हुआ गोला, लेटा हुआ बेलन या शंकु उदासीन संतुलन में होते हैं। सरल शब्दों में, उदासीन संतुलन वाली वस्तुएँ विस्थापन के बाद नई स्थिति में स्थिर रहती हैं, बिना अपने आप लौटे या गिरे।

यह भी पढ़ें – बल आघूर्ण