हम इस संसार में अपने चारों ओर अनेक प्रकार की वस्तुएँ देखते हैं। तथापि, किसी अँधेरे 2 कमरे में हम कुछ भी देखने में असमर्थ हैं। कमरे को प्रकाशित करने पर चीजें दिखलाई देने लगती हैं। वह क्या है जो वस्तुओं को दृश्यमान बनाता है। दिन के समय सूर्य का प्रकाश वस्तुओं को देखने में हमारी सहायता करता है। कोई वस्तु उस पर पड़ने वाले प्रकाश को परावर्तित करती है। यह परावर्तित प्रकाश जब हमारी आँखों द्वारा ग्रहण किया जाता है, तो हमें वस्तुओं को देखने योग्य बनाता है। हम किसी पारदर्शी माध्यम के आर-पार देख सकते हैं, क्योंकि प्रकाश इसमें से पार (transmitted) हो जाता है। प्रकाश से संबद्ध अनेक सामान्य तथा अद्भुत परिघटनाएँ हैं; जैसे- दर्पणों द्वारा प्रतिबिंब का बनना, तारों का टिमटिमाना, इंद्रधनुष के सुंदर रंग, किसी माध्यम द्वारा प्रकाश को मोड़ना आदि। प्रकाश के गुणों का अध्ययन इनके अन्वेषण में हमारी सहायता करेगा। अपने चारों ओर कुछ सामान्य प्रकाशिक परिघटनाओं को देख कर हम यह निष्कर्ष निकाल सकते हैं कि प्रकाश सरल रेखाओं में गमन करता प्रतीत होता है। यह तथ्य कि एक छोटा प्रकाश सोत किसी अपारदर्शी वस्तु की तीक्ष्ण छाया बनाता है, प्रकाश के एक सरलरेखीय पथ की ओर इंगित करता है, जिसे प्रायः प्रकाश किरण कहते हैं।
इस अध्याय में हम प्रकाश के परावर्तन तथा अपवर्तन की परिघटनाओं का, प्रकाश के सरलरेखीय गमन का उपयोग करके, अध्ययन करेंगे। ये मूल धारणाएँ प्रकृति में घटनेवाली कुछ प्रकाशिक परिघटनाओं के अध्ययन में हमारी सहायता करेंगी। इस अध्याय में हम गोलीय दर्पणों द्वारा प्रकाश के परावर्तन, प्रकाश के अपवर्तन एवं वास्तविक जीवन में उनके अनुप्रयोगों को समझने का प्रयत्न करेंगे।
9.1 प्रकाश का परावर्तन
उच्च कोटि की पॉलिश किया हुआ पृष्ठ, जैसे कि दर्पण, अपने पर पड़नेवाले अधिकांश प्रकाश को परावर्तित कर देता है। आप प्रकाश के परावर्तन के नियमों से पहले से ही परिचित हैं। आइए, इन नियमों को स्मरण करें-
(i) आपतन कोण, परावर्तन कोण के बराबर होता है, तथा
(ii) आपतित किरण, दर्पण के आपतन बिंदु पर अभिलंब तथा परावर्तित किरण, सभी एक ही तल में होते हैं।
परावर्तन के ये नियम गोलीय पृष्ठों सहित सभी प्रकार के परावर्तक पृष्ठों के लिए लागू होते हैं। आप समतल दर्पण द्वारा प्रतिबिंब के बनने से परिचित हैं। प्रतिबिंब की क्या विशेषताएँ हैं? समतल दर्पण द्वारा बना प्रतिबिंब सदैव आभासी तथा सीधा होता है। प्रतिबिंब का साइज़ बिंब (वस्तु) के साइज़ के बराबर होता है। प्रतिबिंब दर्पण के पीछे उतनी ही दूरी पर बनता है, जितनी दूरी पर दर्पण के सामने बिंब रखा होता है। इसके अतिरिक्त प्रतिबिंब पार्श्व परिवर्तित होता है। यदि परावर्तक पृष्ठ वक्रित हों तो प्रतिबिब कैस बनेंगे? आइए देखें।
क्रियाकलाप 9.1
• एक बड़ी चमकदार चम्मच लीजिए। इसके बक्रित पृष्ठ में अपना चेहरा देखने का प्रयत्न कीजिए।
• क्या आप प्रतिबिंब देख पाते हैं? यह छोटा है या बड़ा?
• चम्मच को धीरे-धीरे अपने चेहरे से दूर ले जाइए। प्रतिबिंब को देखते रहिए। यह कैसे परिवर्तित होता है?
• चम्मच को उलटा कीजिए (पलटिए) तथा दूसरे पृष्ठ से क्रियाकलाप को दोहराइए। अब प्रतिबिंब कैसा दिखलाई देता है?
• दोनों पृष्ठों पर प्रतिबिंब के अभिलक्षणों की तुलना कीजिए।
चमकदार चम्मच का वक्रित पृष्ठ एक वक्रित दर्पण की भाँति माना जा सकता है। सबसे अधिक उपयोग में आने वाले सामान्यतः वक्रित दर्पण का प्रारूप गोलीय दर्पण है। इस प्रकार के दर्पणों के परावर्तक पृष्ठ किसी गोले के पृष्ठ का एक भाग माना जा सकता है। ऐसे दर्पण जिनका परावर्तक पृष्ठ गोलीय है, गोलीय दर्पण कहलाते हैं। अब हम गोलीय दर्पणों के बारे में कुछ विस्तार से अध्ययन करेंगे।
9.2 गोलीय दर्पण
गोलीय दर्पण का परावर्तक पृष्ठ अंदर की ओर या बाहर की ओर वक्रित हो सकता है। गोलीय दर्पण, जिसका परावर्तक पृष्ठ अंदर की ओर अर्थात गोल के केंद्र की ओर वक्रित है, वह अवतल दर्पण कहलाता है। वह गोलीय दर्पण जिसका परावर्तक पृष्ठ बाहर की ओर वक्रित है, उत्तल दर्पण कहलाता है। इन दर्पणों का आरेखीय निरूपण चित्र 9.1 में किया गया है। इन चित्रों में नोट कीजिए कि दर्पणों का पृष्ठभाग छायांकित है।
अब आप समझ सकते हैं कि चम्मच का अंदर की ओर वक्रित पृष्ठ लगभग अवतल दर्पण जैसा है तथा चम्मच का बाहर की ओर उभरा पृष्ठ लगभग उत्तल दर्पण जैसा है।
गोलीय दर्पणों के बारे में और अधिक ज्ञान प्राप्त करने से पहले आइए हम कुछ शब्दों अथवा पों (terms) को जानें तथा उनका अर्थ समझें। ये शब्द गोलीय दर्पणों के बारे में चर्चा करते समय सामान्यतः प्रयोग में आते हैं। गोलीय दर्पण के परावर्तक पृष्ठ के केंद्र को दर्पण का ध्रुब कहते हैं। यह दर्पण के पृष्ठ पर स्थित होता है। ध्रुव को प्रायः P अक्षर से निरूपित करते हैं।
गोलीय दर्पण का परावर्तक पृष्ठ एक गोले का भाग है। इस गोले का केंद्र गोलीय दर्पण का वक्रता केंद्र कहलाता है। यह अक्षर C से निरूपित किया जाता है। कृपया ध्यान दें कि वक्रता केंद्र दर्पण का भाग नहीं है। यह परावर्तक पृष्ठ के बाहर स्थित है। अवतल दर्पण का वक्रता केंद्र परावर्तक पृष्ठ के सामने स्थित होता है। तथापि, उत्तल दर्पण में यह दर्पण के परावर्तक पृष्ठ के पीछे स्थित होता है। यह तथ्य आप चित्र 9.2 (a) तथा 9.2 (b) में नोट कर सकते हैं। गोलीय दर्पण का परावर्तक पृष्ठ जिस गोले का भाग है, उसकी त्रिज्या दर्पण की वक्रता त्रिज्या कहलाती है। इसे अक्षर R से निरूपित किया जाता है। ध्यान दीजिए कि PC दूरी वक्रता त्रिज्या के बराबर है। गोलीय दर्पण के ध्रुव तथा वक्रता त्रिज्या से गुजरने वाली एक सीधी रेखा की कल्पना कीजिए। इस रेखा को दर्पण का मुख्य अक्ष कहते हैं। याद कीजिए कि मुख्य अक्ष दर्पण के ध्रुव पर अभिलंब है। आइए, दर्पण से संबंधित एक महत्वपूर्ण शब्द को एक क्रियाकलाप द्वारा समझें।

सर्वप्रथम कागज़ सुलगना प्रारंभ करता है और धुआँ उठने लगता है। अंततः यह आग भी पकड़ सकता है। यह क्यों जलता है? सूर्य से आने वाला प्रकाश दर्पण के द्वारा एक तीक्ष्ण, चमकदार बिंदु के रूप में अभिकेंद्रित होता है। वास्तव में कागज़ की शीट पर प्रकाश का यह बिंदु सूर्य का प्रतिबिंब है। यह बिंदु अवतल दर्पण का फोकस है। सूर्य के प्रकाश के संकेंद्रण से उत्पन्न ऊष्मा के कारण कागज़ जलता है। दर्पण की स्थिति से इस प्रतिबिंब की दूरी, दर्पण की फोकस दूरी का सन्निकट मान है।
क्रियाकलाप 9.2
चेताबनी- सूर्य की ओर या दर्पण द्वारा परावर्तित सूर्य के प्रकाश की ओर सीधा मत देखिए। यह आपकी आँखों को क्षतिग्रस्त कर सकता है।
एक अवतल दर्पण को अपने हाथ में पकड़िए तथा इसके परावर्तक पृष्ठ को सूर्य की ओर कीजिए। दर्पण द्वारा परावर्तित प्रकाश को दर्पण के पास रखी एक कागज़ की शीट पर डालिए। कागज़ की शीट को धीरे-धीर आगे पीछे कीजिए जब तक कि आपको कागज़ की शीट पर प्रकाश का एक चमकदार, तीक्ष्ण बिंदु प्राप्त न हो जाए। दर्पण तथा कागज़ को कुछ मिनट के लिए उसी स्थिति में पकड़े रखिए। आप क्या देखते हैं? ऐसा क्यों होता है?

चित्र 9.2 (a)अवतल दर्पण (b) उत्तल दर्पण
आइए, इस प्रेक्षण को एक किरण आरेख से समझने का प्रयत्न करें। चित्र 9.2 (a) को ध्यानपूर्वक देखिए। अवतल दर्पण पर मुख्य अक्ष के समांतर कुछ किरणें आपतित हो रही हैं। परावर्तित किरणों का प्रेक्षण कीजिए। वे सभी दर्पण की मुख्य अक्ष के एक बिंदु पर मिल रही प्रतिच्छेदी हैं। यह बिंदु अवतल दर्पण का मुख्य फोकस कहलाता है। इसी प्रकार चित्र 9.2 (b) को ध्यानपूर्वक देखिए। उत्तल दर्पण द्वारा मुख्य अक्ष के समांतर किरणें किस प्रकार परावर्तित होती हैं? परावर्तित किरणें मुख्य अक्ष पर एक बिंदु से आती हुई प्रतीत होती हैं। यह बिंदु उत्तल दर्पण का मुख्य फोकस कहलाता है। मुख्य फोकस को अक्षर F द्वारा निरूपित किया जाता है। गोलीय दर्पण के ध्रुव तथा मुख्य फोकस के बीच की दूरी फोकस दूरी कहलाती है। इसे अक्षर f द्वारा निरूपित करते हैं।
गोलीय दर्पण का परावर्तक पृष्ठ अधिकांशतः गोलीय ही होता है। इस पृष्ठ की एक वृत्ताकार सीमा रेखा होती है। गोलीय दर्पण के परावर्तक पृष्ठ की इस वृत्ताकार सीमारेखा का व्यास, दर्पण का द्वारक (aperture) कहलाता है। चित्र 9.2 में दूरी MN द्वारक को निरूपित करती है। अपने विवेचन में हम केवल उन्हीं गोलीय दर्पणों पर विचार करेंगे, जिनका द्वारक इनकी वक्रता त्रिज्या से बहुत छोटा है।
क्या गोलीय दर्पण की वक्रता त्रिज्या R तथा फोकस दूरी के बीच कोई संबंध है? छोटे द्वारक के गोलीय दर्पणों के लिए वक्रता त्रिज्या फोकस दूरी से दोगुनी होती है। हम इस संबंध को R = 2f द्वारा व्यक्त कर सकते हैं। यह दर्शाता है कि किसी गोलीय दर्पण का मुख्य फोकस, उसके ध्रुव तथा वक्रता के केंद्र को मिलाने वाली रेखा का मध्य बिंदु होता है।
9.2.1 गोलीय दर्पणों द्वारा प्रतिबिंब बनना
आप समतल दर्पणों द्वारा प्रतिबिंब बनने के बारे में अध्ययन कर चुके हैं। आप उनके द्वारा बनाए गए प्रतिबिंबों की प्रकृति, स्थिति तथा आपेक्षिक साइज़ के बारे में भी जानते हैं। गोलीय दर्पणां द्वारा बने प्रतिबिंब कैसे होते हैं? किसी अवतल दर्पण द्वारा बिंब की विभिन्न स्थितियों के लिए बने प्रतिबिंबों की स्थिति का निर्धारण हम किस प्रकार कर सकते हैं? ये प्रतिबिंब वास्तविक हैं अथवा आभासी? क्या वे आवर्धित हैं, छोटे हैं या समान साइज़ के हैं? हम एक क्रियाकलाप द्वारा इसका अन्वेषण करेंगे।
क्रियाकलाप 9.3
• अवतल दर्पण की फोकस दूरी ज्ञात करने की विधि पहले ही सीख चुके हैं। क्रियाकलाप 9.2 में आपने देखा है कि आपको कागज़ पर मिला प्रकाश का तीक्ष्ण चमकदार बिंदु वास्तव में सूर्य का प्रतिबिंब है। यह अत्यंत छोटा, वास्तविक तथा उलटा है। दर्पण से इस प्रतिबिंब की दूरी माप कर आपने अवतल दर्पण की लगभग फोकस दूरी ज्ञात की थी।
• एक अवतल दर्पण लीजिए। ऊपर वर्णित विधि से इसकी सन्निकट फोकस दूरी ज्ञात कीजिए। फोकस दूरी का मान नोट कीजिए। (आप किसी दूरस्थ वस्तु का प्रतिबिंब एक कागज़ की शीट पर प्राप्त करके भी फोकस दूरी ज्ञात कर सकते हैं।)
• मेज़ पर चॉक से एक लाइन बनाइए। अवतल दर्पण को एक स्टैंड पर रखिए। स्टैंड को लाइन पर इस प्रकार रखिए कि दर्पण का ध्रुव इस लाइन पर स्थित हो।
• चॉक से पहली लाइन के समांतर और इसके आगे, दो लाइनें इस प्रकार खींचिए कि किन्हीं दो उत्तरोत्तर लाइनों के बीच की दूरी दर्पण की फोकस दूरी के बराबर हो। ये लाइनें अब क्रमशः बिंदुओं P, F तथा C की स्थितियों के तदनुरूपी होंगी। याद रखिए- छोटे द्वारक के गोलीय दर्पण के लिए मुख्य फोकस F, ध्रुव P तथा वक्रता केंद्र C को मिलाने वाली रेखा के मध्य बिंदु पर स्थित होता है।
• एक चमकीला बिंब, जैसे एक जलती हुई मोमबत्ती C से बहुत दूर किसी स्थिति पर रखिए। एक कागज़ का परदा रखिए तथा इसको दर्पण के सामने आगे-पीछे तब तक खिसकाइए जब तक कि आपको इस पर मोमबत्ती की लो का तीक्ष्ण तथा चमकीला प्रतिबिंब प्राप्त न हो जाए। प्रतिबिंब को ध्यानपूर्वक देखिए। इसकी प्रकृति, स्थिति तथा बिंब के साइज़ के सापेक्ष इसका आपेक्षिक साइज़ नोट कीजिए।
• इस क्रियाकलाप को मोमबत्ती की निम्नलिखित स्थितियों के लिए दोहराइए- (a) C से थोड़ी दूर, (b) C पर, (c) F तथा C के बीच, (d) F पर तथा (e) P और F के बीच।
• इनमें से एक स्थिति में आप परदे पर प्रतिबिंब प्राप्त नहीं कर पाएँगे। इस अवस्था में बिंब की स्थिति को अभिनिर्धारित कीजिए। तब, इसके आभासी प्रतिबिंब को सीधे दर्पण में देखिए।
• अपने प्रेक्षणों को नोट कीजिए तथा सारणीबद्ध कीजिए।
उपरोक्त क्रियाकलाप में आप देखेंगे कि अवतल दर्पण द्वारा बने प्रतिबिंब की प्रकृति, स्थिति तथा साइज़ बिंदु P, F तथा C के सापेक्ष बिंब की स्थिति पर निर्भर करते है। बिंब की कुछ स्थितियों के लिए बनने वाला प्रतिबिंब वास्तविक है। बिंब की कुछ दूसरी स्थितियों के लिए यह आभासी होता है। बिंब की स्थिति के अनुसार ही प्रतिबिंब आवर्धित, छोटा या समान साइज़ का होता है। इन प्रेक्षणों का संक्षिप्त विवरण, आपके निर्देशन के लिए सारणी 9.1 में दिया गया है।
सारणी 9.1 किसी अवतल दर्पण द्वारा बिंब की विभिन्न स्थितियों के लिए बने प्रतिबिंब

9.2.2 किरण आरेखों का उपयोग करके गोलीय दर्पणों द्वारा बने प्रतिबिंबों का निरूपण
गोलीय दर्पणों द्वारा प्रतिबिंबों के बनने का अध्ययन हम किरण आरेख खींचकर भी कर सकते हैं। गोलीय दर्पण के सामने रखे एक सीमित साइज़ के विस्तारित बिंब पर विचार कीजिए। इस बिंब का प्रत्येक छोटा भाग एक बिंदु बिंब की भाँति कार्य करता है। इन बिंदुओं में प्रत्येक से अनंत किरणें उत्पन्न होती हैं। बिंब के प्रतिबिंब का स्थान निर्धारण करने के लिए, किरण आरेख बनाते समय किसी बिंदु से निकलने वाली किरणों की विशाल संख्या में से सुविधानुसार कुछ को चुना जा सकता है। तथापि, किरण आरेख की स्पष्टता के लिए दो किरणों पर विचार करना अधिक सुविधाजनक है। ये किरणें ऐसी हों कि दर्पण से परावर्तन के पश्चात उनकी दिशाओं को जानना आसान हो।
कम-से-कम दो परावर्तित किरणों के प्रतिच्छेदन से किसी बिंदु बिंब के प्रतिबिंब की स्थिति ज्ञात की जा सकती है। प्रतिबिंब के स्थान निर्धारण के लिए निम्नलिखित में से किन्हीं भी दो किरणों पर विचार किया जा सकता है।
(i) दर्पण के मुख्य अक्ष के समानांतर प्रकाश किरण, परावर्तन के पश्चात अवतल दर्पण के मुख्य फोकस से गुज़रेगी अथवा उत्तल दर्पण के मुख्य फोकस से अपसरित होती प्रतीत होगी। यह चित्र 9.3 (a) एवं (b) में दर्शाया गया है।

(ii) अवतल दर्पण के मुख्य फोकस से गुजरने वाली किरण अथवा उत्तल दर्पण के मुख्य फोकस की ओर निर्देशित किरण परावर्तन के पश्चात मुख्य अक्ष के समांतर निकलेगी। इसे चित्र 9.4 (a) तथा चित्र 9.4 (b) में दर्शाया गया है।

(iii) अवतल दर्पण के वक्रता केंद्र से गुजरने वाली किरण अथवा उत्तल दर्पण के वक्रता केंद्र की ओर निर्देशित किरण, परावर्तन के पश्चात उसी पथ के अनुदिश वापस परावर्तित हो जाती है। इसे चित्र 9.5 (a) तथा 9.5 (b) में दर्शाया गया है। प्रकाश की किरणें उसी पथ से इसलिए वापस आती हैं, क्योंकि आपतित किरणें दर्पण के परावर्तक पृष्ठ पर अभिलंब के अनुदिश पड़ती हैं।

(iv) अवतल दर्पण चित्र 9.6 (a) अथवा उत्तल दर्पण चित्र 9.6 (b) के बिंदु P (दर्पण का ध्रुव) की ओर मुख्य अक्ष से तिर्यक दिशा में आपतित किरण, तिर्यक दिशा में ही परावर्तित होती है। आपतित तथा परावर्तित किरणें आपतन बिंदु (बिंदु P) पर मुख्य अक्ष से समान कोण बनाते हुए परावर्तन के नियमों का पालन करती हैं।

याद रखिए कि उपरोक्त सभी स्थितियों में परावर्तन के नियमों का पालन होता है। आपतन बिंदु पर आपतित किरण इस प्रकार परावर्तित होती है कि परावर्तन कोण का मान सदैव आपतन कोण के मान के बराबर हो।
(a) अवतल दर्पण द्वारा प्रतिबिंब बनना
चित्र 9.7 (a) से (f) में बिंब की विभिन्न स्थितियों के लिए अवतल दर्पण द्वारा प्रतिबिंब का बनना किरण आरेखों द्वारा दर्शाया गया है।

क्रियाकलाप 9.4
• सारणी 9.1 में दर्शाई गई बिंब की प्रत्येक स्थिति के लिए स्वच्छ किरण आरेख खीचिए।
• प्रतिबिंब का स्थान निर्धारित करने के लिए आप पूर्व अनुच्छेद में वर्णित कोई दो किरणें ले सकते हैं।
• अपने चित्रों की तुलना चित्र 9.7 में दिए गए चित्रों से कीजिए।
• प्रत्येक दशा में बनने वाले प्रतिबिंब की प्रकृति, स्थिति तथा आपेक्षिक साइज़ का वर्णन कीजिए।
• अपने परिणामों को सुविधाजनक प्रारूप में सारणीबद्ध कीजिए।
अवतल दर्पणों के उपयोग
अवतल दर्पणों का उपयोग सामान्यतः टॉर्च, सर्चलाइट तथा वाहनों के अग्रदीपों (headlights) में प्रकाश का शक्तिशाली समानांतर किरण पुंज प्राप्त करने के लिए किया जाता है। इन्हें प्रायः चेहरे का बड़ा प्रतिबिंब देखने के लिए शेविंग दर्पणों (shaving mirrors) के रूप में उपयोग करते हैं। दंत विशेषज्ञ अवतल दर्पणों का उपयोग मरीजों के दाँतों का बड़ा प्रतिबिंब देखने के लिए करते हैं। सौर भट्टियों में सूर्य के प्रकाश को केंद्रित करने के लिए बड़े अवतल दर्पणों का उपयोग किया जाता है।
(b) उत्तल दर्पण द्वारा प्रतिबिंब बनना
हमने अवतल दर्पण द्वारा प्रतिबिंब बनने के बारे में अध्ययन किया है। अब हम उत्तल दर्पण द्वारा प्रतिबिंब बनने के बारे में अध्ययन करेंगे।
क्रियाकलाप 9.5
• कोई उत्तल दर्पण लीजिए। इसे एक हाथ में पकड़िए।
• दूसरे हाथ में एक सीधी खड़ी पेंसिल पकड़िए।
• दर्पण में पेंसिल का प्रतिबिंब देखिए। प्रतिबिंब सीधा है या उल्टा? क्या यह छोटा है अथवा विवर्धित (बड़ा) है?
• पेंसिल को धीर-धीरे दर्पण से दूर ले जाइए। क्या प्रतिबिंब छोटा होता जाता है या बड़ा होता जाता है?
• क्रियाकलाप को सावधानीपूर्वक दोहराइए। बताइए कि जब बिंब को दर्पण से दूर ले जाते हैं तो प्रतिबिंब फोकस के निकट आता है अथवा उससे और दूर चला जाता है?
उत्तल दर्पण द्वारा बने प्रतिबिंब का अध्ययन करने के लिए हम बिंब की दो स्थितियों पर विचार करते हैं। पहली स्थिति में बिंब अनंत दूरी पर है तथा दूसरी स्थिति में बिंब दर्पण से एक निश्चित दूरी पर है। बिंब की इन दो स्थितियों के लिए उत्तल दर्पण द्वारा बनाए गए प्रतिबिंबों के किरण आरेखों को क्रमशः चित्र 9.8 (a) तथा 9.8 (b) में दर्शाया गया है। परिणामों का संक्षिप्त विवरण सारणी 9.2 में दिया गया है।

सारणी 9.2 उत्तल दर्पण द्वारा बने प्रतिबिंब की प्रकृति, स्थिति तथा आपेक्षिक साइज़
| बिंब की स्थिति | प्रतिबिंब की स्थिति | प्रतिबिंब का साइज | प्रतिबिंब की प्रकृति |
| अनंत पर | फोकस F पर दर्पण के पीछे | अत्यधिक छोटा, बिंदु के साइज का | आभाषी तथा सीधा |
| अनंत तथा दर्पण के ध्रुव P के बीच | P तथा F के बीच | छोटा | आभाषी तथा सीधा |
अभी तक आपने समतल दर्पण, अवतल दर्पण तथा उत्तल दर्पण द्वारा प्रतिबिंब बनाने के बारे में अध्ययन किया है। इनमें से कौन-सा दर्पण किसी बड़े बिंब का पूरा प्रतिबिंब बनाएगा? आइए एक क्रियाकलाप द्वारा इसका अन्वेषण करें।
क्रियाकलाप 9.6
• समतल दर्पण में किसी दूरस्थ बिंब जैसे कोई दूरस्थ पेड़ का प्रतिबिंब देखिए।
• क्या आप पूर्ण-लंबाई (full-length) का प्रतिबिंब देख पाते हैं?
• विभिन्न साइज़ के समतल दर्पण लेकर प्रयोग दोहराइए। क्या आप दर्पण में बिंब का संपूर्ण प्रतिबिंब देख पाते हैं?
• इस क्रियाकलाप को अवतल दर्पण लेकर दोहराइए। क्या यह दर्पण बिंब की पूरी लंबाई का प्रतिबिंब बना पाता है?
• अब एक उत्तल दर्पण लेकर इस प्रयोग को दोहराइए। क्या आपको सफलता मिली? अपने प्रेक्षणों की कारण सहित व्याख्या कीजिए।
आप एक छोटे उत्तल दर्पण में किसी ऊँचे भवन/पेड़ का पूर्ण-लंबाई का प्रतिबिंब देख सकते हैं। आगरा किले की एक दीवार में ऐसा ही एक दर्पण ताजमहल की ओर लगा हुआ है। यदि आप कभी आगरा किला देखने जाएँ तो दीवार में लगे इस दर्पण में ताजमहल के पूरे प्रतिबिंब को देखने का प्रयास करें। मकबरे को स्पष्टतः देखने के लिए आपको दीवार से सटी हुईं छत पर उचित स्थान पर खड़ा होना होगा।
उत्तल दर्पणों के उपयोग
उत्तल दर्पणों का उपयोग सामान्यतः वाहनों के पश्च-दृश्य (wing) दर्पणों के रूप में किया जाता है। ये दर्पण वाहन के पार्श्व (side) में लगे होते हैं तथा इनमें ड्राइवर अपने पीछे के वाहनों को देख सकते हैं, जिससे वे सुरक्षित रूप से वाहन चला सकें। उत्तल दर्पणों को इसलिए भी प्राथमिकता देते हैं, क्योंकि ये सदैव सीधा प्रतिबिंब बनाते हैं। यद्यपि वह छोटा होता है। इनका दृष्टि-क्षेत्र भी बहुत अधिक है, क्योंकि ये बाहर की ओर वक्रित होते हैं। अतः समतल दर्पण की तुलना में उत्तल दर्पण ड्राइवर को अपने पीछे के बहुत बड़े क्षेत्र को देखने में समर्थ बनाते हैं।
9.2.3 गोलीय दर्पणों द्वारा परावर्तन के लिए चिह्न परिपाटी
गोलीय दर्पणों द्वारा प्रकाश के परावर्तन पर विचार करते समय हम एक निश्चित चिह्न परिपाटी का पालन करेंगे, जिसे नई कार्तीय चिह्न परिपाटी कहते हैं। इस परिपाटी में दर्पण के ध्रुव (P) (चित्र
(9.9) को मूल बिंदु मानते हैं। दर्पण के मुख्य अक्ष को निर्देशांक पद्धति का x-अक्ष (xx’) लिया जाता है। यह परिपाटी निम्नलिखित प्रकार की है-
(i) बिंब सदैव दर्पण के बाईं ओर रखा जाता है। इसका अर्थ है कि दर्पण पर बिंब से प्रकाश बाईं ओर से आपतित होता है।
(ii) मुख्य अक्ष के समानांतर सभी दूरियाँ दर्पण के ध्रुव से मापी जाती हैं।
(iii) मूल बिंदु के दाईं ओर (+ x-अक्ष के अनुदिश) मापी गई सभी दरियाँ धनात्मक मानी जाती हैं, जबकि मूल बिंदु के बाईं ओर (-x-अक्ष के अनुदिश) मापी गई दूरियाँ ऋणात्मक मानी। जाती हैं।
(iv) मुख्य अक्ष के लंबवत तथा ऊपर की ओर (+ y-अक्ष के अनुदिश) मापी जाने वाली दूरियाँ धनात्मक मानी जाती हैं।
(v) मुख्य अक्ष के लंबवत तथा नीचे की ओर (- y-अक्ष के अनुदिश) मापी जाने वाली दूरियाँ ऋणात्मक मानी जाती हैं।

ऊपर वर्णित नई कार्तीय चिह्न परिपाटी आपके संदर्भ के लिए चित्र 9.9 में दर्शाई गई है। यह चिह्न परिपाटी दर्पण का सूत्र प्राप्त करने तथा संबंधित आंकिक प्रश्नों को हल करने के लिए प्रयुक्त की गई है।
9.2.4 दर्पण सूत्र तथा आवर्धन
गोलीय दर्पण में इसके ध्रुव से बिंब की दूरी, बिंब दूरी (1) कहलाती है। दर्पण के ध्रुव से प्रतिबिंब की दूरी, प्रतिबिंब दूरी (v) कहलाती है। आपको पहले ही ज्ञात है कि ध्रुव से मुख्य फोकस की दूरी, फोकस दूरी (1) कहलाती है। इन तीनों राशियों के बीच एक संबंध है, जिसे दर्पण सूत्र द्वारा प्रस्तुत किया जाता है।
इस सूत्र को निम्नलिखित प्रकार से व्यक्त करते हैं-
1/v + 1/u = 1/f (9.1)
यह संबंध सभी प्रकार के गोलीय दर्पणों के लिए तथा बिंब की सभी स्थितियों के लिए मान्य हैं। प्रश्नों को हल करते समय, जब आप दर्पण सूत्र में u, v, f तथा R के मान प्रतिस्थापित करें तो आपको नई कार्तीय चिह्न परिपाटी का प्रयोग करना चाहिए।
आवर्धन
गोलीय दर्पण द्वारा उत्पन्न आवर्धन वह आपेक्षिक विस्तार है, जिससे ज्ञात होता है कि कोई प्रतिबिंब बिंब की अपेक्षा कितना गुना आवर्धित है। इसे प्रतिबिंब की ऊँचाई तथा बिंब की ऊँचाई के अनुपात रूप में व्यक्त किया जाता है।
यदि h बिंब की ऊँचाई हो तथा h’ प्रतिबिंब की ऊँचाई हो तो गोलीय दर्पण द्वारा उत्पन्न आवर्धन (m) प्राप्त होगा।
m = प्रतिबिंब की ऊँचाई (h’) / बिंब की ऊंचाई (h)
m = h’/h (9.2)
आवर्धन m बिंब दूरी (u) तथा प्रतिबिंब दूरी (v) से भी संबंधित है। इसे व्यक्त किया जाता है-
आवर्धन (m) = h’/h = -v/u (9.3)
ध्यान दीजिए, बिंब की ऊँचाई धनात्मक ली जाती है, क्योंकि बिंब प्रायः मुख्य अक्ष के ऊपर रखा जाता है। आभासी प्रतिबिंबों के लिए बिंब की ऊँचाई धनात्मक लेनी चाहिए। तथापि वास्तविक प्रतिबिंबों के लिए इसे ऋणात्मक लेना चाहिए। आवर्धन के मान में ऋणात्मक चिह्न से ज्ञात होता है कि प्रतिबिंब वास्तविक है। आवर्धन के मान में धनात्मक चिह्न बताता है कि प्रतिबिंब आभासी है।
उदाहरण 9.1 किसी ऑटोमोबाइल में पीछे का दृश्य देखने के लिए उपयोग होने वाले उत्तल दर्पण की वक्रता त्रिज्या 3.00 m है। यदि एक बस इस दर्पण से 5.00m की दूरी पर स्थित है तो प्रतिबिंब की स्थिति, प्रकृति तथा साइज ज्ञात कीजिए।
हल:
वक्रता त्रिज्या, R = + 3.00 m;
बिंब-दरी, u = – 5.00 m;
प्रतिबिंब-दूरी, v = ?
प्रतिबिंब की ऊँचाई, h’ =?
फोकस दूरी f = R/2 = + 3.00m/2 = +1.5m क्योंकि उत्तल दर्पण का मुख्य फोकस दर्पण के पीछे है।)
क्योंकि 1/v + 1/u = 1/f
या 1/v = 1/f – 1/u = + 1/1.5 – 1/(-5) = 1/1.5 + 1/5
(5 + 1.5)/7.5
v = +7.5/6.5 = + 1.15m
प्रतिबिंब दर्पण के पीछे 1.15 m की दूरी पर है।
आवर्धन, m = h’/h = -v/u = – 1.15m/ (-5)m
= +0.23
प्रतिबिंब आभासी, सीधा तथा साइन में बिंब से छोटा (0.23 गुना) है।
उदाहरण 9.2 कोई 4.0 cm साइज़ का बिंब किसी 15.0 cm फोकस दूरी के अवतल दर्पण से 25.0 cm दूरी पर रखा है। दर्पण से कितनी दूरी पर किसी परदे को रखा जाए कि स्पष्ट प्रतिबिंब प्राप्त हो? प्रतिबिंब की प्रकृति तथा साइज ज्ञात कीजिए।
हल :
बिंब-साइज़, h = + 4.0 cm;
बिंब-दूरी, u = – 25.0 cm;
फोकस दूरी f= -15.0 cm;
प्रतिबिंब-दरी, v = ?
प्रतिबिंब-साइज़, h’ =?
समीकरण (9.1) से
1/v + 1/u = 1/f
या 1/v = 1/f – 1/u = 1/(-15) – 1/(-25)
= – 1/15 + 1/25
या 1/v = (-5+3)/75 = -2/75
या v = -37.5 cm
परदे को दर्पण के सामने 37.5 cm दूरी पर रखना चाहिए। प्रतिबिंब वास्तविक है।
इसी प्रकार, आवर्धन, m = h’/h = -v/u
या h’ = – vh/u = – (-37.5cm)(+4.0)/(-25cm)
प्रतिबिंब की ऊंचाई, h’ = -6.0 cm
प्रतिबिंब उल्टा तथा आवर्धित है।
9.3 प्रकाश का अपवर्तन
किसी पारदर्शी माध्यम में प्रकाश सरल रेखा में गमन करता प्रतीत होता है। जब प्रकाश एक पारदर्शी माध्यम से दूसरे में प्रवेश करता है तो क्या होता है? क्या यह अब भी सरल रेखा में चलता है या अपनी दिशा बदलता है? हम अपने दिन-प्रतिदिन के कुछ अनुभवों को दोहराएँगे। आपने देखा होगा कि पानी से भरे किसी टैंक अथवा ताल या पोखर की तली उठी हुई प्रतीत होती है। इसी प्रकार, जब कोई मोटा काँच का स्लैब (सिल्ली) किसी मुद्रित सामग्री पर रखा जाता है, तो काँच के स्लैब के ऊपर से देखने पर अक्षर उठे हुए प्रतीत होते हैं। ऐसा क्यों होता है?
क्या आपने किसी काँच के बर्तन में रखे पानी में किसी पेंसिल को आंशिक रूप से डूबे देखा है? यह वायु तथा पानी के अंतरपृष्ठ पर (अर्थात पानी की ऊपरी सतह पर) टेढ़ी प्रतीत होती है।
आपने देखा होगा कि पानी से भरे किसी काँच के बर्तन में रखे नींबू पार्श्व (side) से देखने पर अपने वास्तविक साइज़ से बड़े प्रतीत होते हैं। इन अनुभवों की व्याख्या आप किस प्रकार करेंगे?
आइए, पानी में आंशिक रूप से डूबी पेंसिल के मुड़े होने की घटना पर विचार करें। पेंसिल के पानी में डूबे भाग से आपके पास पहुँचने वाला प्रकाश, पेंसिल के पानी से बाहर के भाग की तुलना में भिन्न दिशा से आता हुआ प्रतीत होता है। इसी कारण पेंसिल मुड़ी हुई प्रतीत होती है। इन्ही कारणों से, जब अक्षरों के ऊपर काँच का स्लैब रखकर देखते हैं तो वे उठे हुए प्रतीत होते हैं।
यदि पानी के स्थान पर हम कोई अन्य द्रव जैसे किरोसिन या तारपीन का तेल प्रयोग करें, क्या तब भी पेंसिल उतनी ही मुड़ी हुई दिखेगी? यदि हम काँच के स्लैब को पारदर्शी प्लास्टिक के स्लैब से प्रतिस्थापित कर दें, क्या तब भी अक्षर उसी ऊँचाई तक उठे प्रतीत होगे? आप देखेंगे कि अलग-अलग माध्यमों के युग्मों के लिए इन प्रभावों का विस्तार अलग-अलग है। ये प्रेक्षण सूचित करते हैं कि प्रकाश सभी माध्यमों में एक ही दिशा में गमन नहीं करता। ऐसा प्रतीत होता है कि जब प्रकाश एक माध्यम से दूसरे माध्यम में तिरछा होकर जाता है तो दूसरे माध्यम में इसके संचरण की दिशा परिवर्तित हो जाती है। इस परिघटना को विस्तार से कुछ क्रियाकलाप करके समझें।
क्रियाकलाप 9.7
• पानी से भरी एक बाल्टी की तली पर एक सिक्का रखिए।
• अपनी आँख को पानी के ऊपर, किसी पार्श्व (side) में रखकर सिक्के को एक बार में उठाने का प्रयत्न कीजिए। क्या आप सिक्का उठाने में सफल हो पाते हैं?
• इस क्रियाकलाप को दोहराइए। आप इसे एक बार में करने में क्यों सफल नहीं हो पाए थे?
• अपने मित्रों से इसे करने के लिए कहिए। उनके साथ अपने अनुभव की तुलना कीजिए।
क्रियाकलाप 9.8
• किसी मेज़ पर एक बड़ा उथला कटोरा रखकर उसकी तली में एक सिक्का रखिए।
• कटारे से धीरे-धीरे दूर हटिए। जब सिक्का ठीक दिखाई देना बंद हो जाए तो रुक जाइए।
• अपने मित्र से सिक्के को विक्षुब्ध किए बगैर कटोरे में पानी डालने को कहिए।
• अपनी स्थिति से सिक्के को देखते रहिए। क्या सिक्का उसी स्थिति से पुनः दिखाई देने लगता है? यह कैसे संभव हो पाता है?
कटोरे में पानी डालने पर सिक्का फिर से दिखलाई देने लगता है। प्रकाश के अपवर्तन के कारण सिक्का अपनी वास्तविक स्थिति से थोड़ा-सा ऊपर उठा हुआ प्रतीत होता है।
क्रियाकलाप 9.9
• मेज़ पर रखे एक सफ़ेद कागज़ की शीट पर एक मोटी सीधी रेखा खीचिए।
• इस रेखा के ऊपर एक काँच का स्लैब इस प्रकार रखिए कि इसकी एक कोर इस रेखा से कोई कोण बनाए।
• स्लैब के नीचे आए रेखा के भाग को पार्श्व (side) से देखिए। आप क्या देखते हैं? क्या काँच के स्लैब के नीचे की रेखा कोरों (edges) के पास मुड़ी हुई प्रतीत होती है?
• अब काँच के स्लैब को इस प्रकार रखिए कि यह रेखा के अभिलंबवत हो। अब आप क्या देखते हैं? क्या काँच के स्लैब के नीचे रेखा का भाग मुड़ा हुआ प्रतीत होता है?
• रेखा को काँच के स्लैब के ऊपर से देखिए। क्या स्लैब के नीचे रेखा का भाग उठा हुआ प्रतीत होता है? ऐसा क्यों होता है?
9.3.1 काँच के आयताकार स्लैब से अपवर्तन
काँच के स्लैब से प्रकाश के अपवर्तन की परिघटना को समझने के लिए आइए, एक क्रियाकलाप करें।
क्रियाकलाप 9.10
• एक ड्राइंग बोर्ड पर सफेद कागज की एक शीट, ड्राइंग पिनों की सहायता से लगाइए।
• शीट के ऊपर बीच में काँच का एक आयताकार स्लैब रखिए।
• पेंसिल से स्लैब की रूपरेखा खींचिए। इस रूपरेखा का नाम ABCD रखते हैं।
• चार एकसमान ऑलपिन लीजिए।
• दो पिर्ने, मान लीजिए E तथा F ऊर्ध्वाधरतः इस प्रकार लगाइए कि पिनों को मिलाने वाली रेखा कोर AB से कोई कोण बनाती हुई हो।
• पिन E तथा F के प्रतिबिंबों को विपरीत फलक से देखिए। दूसरी दो पिनों, माना G तथा H, को इस प्रकार लगाइए कि ये पिर्ने एवं E तथा F के प्रतिबिंब एक सीधी रेखा पर स्थित हो।
• पिनों तथा स्लैब को हटाइए।
• पिनों E तथा F की नोकों (tip) की स्थितियों को मिलाइए तथा इस रेखा को AB तक बढ़ाइए। मान लीजिए EF, AB से बिंदु पर मिलती है। इसी प्रकार पिनों G तथा H की नोकों की स्थितियों को मिलाइए तथा इस रेखा को कोर CD तक बढ़ाइए। मान लीजिए HG, CD से O’ पर मिलती है।
• O तथा O’ को मिलाइए। EF को भी P तक बढ़ाइए, जैसा कि चित्र 9.10 में बिंदुकित रेखा द्वारा दर्शाया गया है।
इस क्रिया इस क्रियाकलाप में आप नोट करेंगे कि प्रकाश किरण ने अपनी दिशा बिंदुओं O तथा O’ पर परिवर्तित की है। नोट कीजिए कि दोनों बिंदु O तथा O’ दोनों पारदर्शी माध्यमों को पृथक् करने वाले पृष्ठों पर स्थित हैं। AB के बिंदु O पर एक अभिलंब NN’ खींचिए तथा दूसरा अभिलंब MM’, CD के बिंदु O’ पर खीचिए। बिंदु O पर प्रकाश किरण विरल माध्यम से सघन माध्यम में अर्थात वायु से काँच में प्रवेश कर रही है। नोट कीजिए कि प्रकाश किरण अभिलंब की ओर झुक जाती है। O’ पर, प्रकाश किरण ने काँच से वायु में अर्थात सघन माध्यम से विरल माध्यम में प्रवेश किया है। प्रकाश किरण अभिलंब से दूर मुड़ जाती है। दोनों अपवर्तक सतहों AB तथा CD पर आपतन कोण तथा अपवर्तन कोण के मानों की तुलना कीजिए।

चित्र 9.10 में सतह AB पर एक किरण EP तिरछी आपतित है, जिसे आपतित किरण कहते हैं। OO’ अपवर्तित किरण है तथा O’H निर्गत किरण है। आप देख सकते हैं कि निर्गत किरण, आपतित किरण की दिशा के समानांतर है। ऐसा क्यों होता है? आयाताकार काँच के स्लैब के विपरीत फलकों AB (वायु-काँच अंतरापृष्ठ) तथा CD (काँच-वायु अतंरापृष्ठ) पर प्रकाश किरण के मुड़ने का परिमाण समान तथा विपरीत है। इसी कारण से निर्गत किरण, आपतित किरण के समानांतर निकलती है। तथापि, प्रकाश किरण में थोड़ा सा पाश्विक विस्थापन होता है। यदि प्रकाश किरण दो माध्यमों के अंतरापृष्ठ पर अभिलंबवत आपतित हो तब क्या होगा? स्वयं करके ज्ञात कीजिए।
अब आप प्रकाश के अपवर्तन से परिचित हैं। अपवर्तन प्रकाश के एक पारदर्शी माध्यम से दूसरे में प्रवेश करने पर प्रकाश की चाल में परिवर्तन के कारण होता है। प्रयोग दशति हैं कि प्रकाश का अपवर्तन निश्चित नियमों के आधार पर होता है।
परावर्तन के नियम निम्नलिखित हैं-
(i) आपतित किरण, अपवर्तित किरण तथा दोनों माध्यमों को पृथक् करने वाले पृष्ठ के आपतन बिंदु पर अभिलंब सभी एक ही तल में होते हैं।
(ii) प्रकाश के किसी निश्चित रंग तथा निश्चित माध्यमों के युग्म के लिए आपतन कोण की ज्या तथा अपवर्तन कोण की ज्या का अनुपात स्थिर होता है। इस नियम को स्नेल का अपवर्तन का नियम भी कहते हैं। (यह कोण 0°< i < 90° के लिए सत्य है) यदि । आपतन कोण हो तथा अपवर्तन कोण हो तब
sin t /sin r = स्थिरांक (9.4)
इस स्थिरांक के मान को दूसरे माध्यम का पहले माध्यम के सापेक्ष अपवर्तनांक (refractive index) कहते हैं। आइए, अपवर्तनांक के बारे में कुछ विस्तार से अध्ययन करें।
9.3.2 अपवर्तनांक
आप पहले ही अध्ययन कर चुके हैं कि जब प्रकाश की किरण तिरछी गमन करती हुई एक पारदर्शी माध्यम से दूसरे में प्रवेश करती है तो यह दूसरे माध्यम में अपनी दिशा परिवर्तित कर लेती है। किन्हीं दिए हुए माध्यमों के युग्म के लिए होने वाले दिशा परिवर्तन के विस्तार को अपवर्तनांक के रूप में भी व्यक्त किया जा सकता है, जो समीकरण (9.4) में दाएँ पक्ष में प्रकट होने वाला स्थिरांक है।
अपवर्तनांक को एक महत्वपूर्ण भौतिक राशि, विभिन्न माध्यमों में प्रकाश के संचरण की आपेक्षिक चाल, से संबद्ध किया जा सकता है। यह देखा गया है कि विभिन्न माध्यमों में प्रकाश अलग-अलग चालों से संचरित होता है। निर्वात में प्रकाश 3 × 108 m/s की चाल से चलता है, जो कि प्रकाश की किसी भी माध्यम में हो सकने वाली दुततम चाल है। वायु में प्रकाश की चाल निर्वात की अपेक्षा थोड़ी ही कम होती है। काँच या पानी में यह यथेष्ट रूप से घट जाती है। दो माध्यमों के युग्म के लिए अपवर्तनांक का मान दोनों माध्यमों में प्रकाश की चाल पर निर्भर है, जैसा कि नीचे दिया गया है।
चित्र 9.11 में दर्शाए अनुसार एक प्रकाश की किरण पर विचार करें, जो माध्यम 1 से माध्यम 2 में प्रवेश कर रही है। मान लीजिए कि प्रकाश की चाल माध्यम 1 v1 में तथा माध्यम 2 में v2 है। माध्यम 2 का माध्यम 1 के सापेक्ष अपवर्तनांक, माध्यम 1 में प्रकाश की चाल तथा माध्यम 2 में प्रकाश की चाल के अनुपात द्वारा व्यक्त करते हैं। इसे प्रायः संकेत n21 से निरूपित करत है। इसे समीकरण के रूप में निम्नलिखित प्रकार से व्यक्त करते हैं-
n21 = माध्यम 1 में प्रकाश की चाल/माध्यम 2 में प्रकाश की चाल = v1/v2 (9.5)
इसी तर्क से, माध्यम । का माध्यम 2 के सापेक्ष अपवर्तनांक से निरूपित करते हैं। इसे व्यक्त किया जाता है-
n21 = माध्यम 1 में प्रकाश की चाल/माध्यम 2 में प्रकाश की चाल = v2/v1 (9.6)
यदि माध्यम 1 निर्वात या वायु है, तब माध्यम 2 का अपवर्तनांक निर्वात के सापेक्ष माना जाता है। यह माध्यम का निरपेक्ष अपवर्तनांक कहलाता है। यह केवल n2 से निरूपित किया जाता है। यदि वायु में प्रकाश की चाल c है तथा माध्यम में प्रकाश की चाल v है तब माध्यम का अपवर्तनांक nm होगा

nm = वायु में प्रकाश की चाल /माध्यम में प्रकाश की चाल = c/v (9.7)
माध्यम का निरपेक्ष अपवर्तनांक केवल अपवर्तनांक कहलाता है। सारणी 9.3 में अनेक माध्यमों के अपवर्तनांक दिए गए हैं। सारणी से आपको ज्ञात होगा कि जल का अपवर्तनांक, nw = 1.33 है। इसका अर्थ है कि वायु में प्रकाश का वेग तथा जल में प्रकाश के वेग का अनुपात 1.33 है। इसी प्रकार क्राउन काँच का अपवर्तनांक, ng = 1.52 होता है। ऐसे आँकड़े अनेक स्थानों पर उपयोगी हैं। तथापि आपको इन आँकड़ों को कंठस्थ करने की आवश्यकता नहीं है।
सारणी 9.3: कुछ द्रव्यात्मक माध्यमों के निरपेक्ष अपवर्तनांक
| द्रव्यात्मक माध्यम | अपवर्तनांक |
| वायु | 1.0003 |
| बर्फ़ | 1.31 |
| जल | 1.33 |
| एल्कोहल | 1.36 |
| किरोसिन | 1.44 |
| संगलित क्वार्ट्ज़ | 1.46 |
| तारपीन का तेल | 1.47 |
| बेंजीन | 1.50 |
| क्राउन काँच | 1.52 |
| कनाडा बालसम | 1.53 |
| खनिज नमक | 1.54 |
| कार्बन डाइसल्फाइड | 1.63 |
| सघन फ्लिंट काँच | 1.65 |
| रूबी (मणिक्य) | 1.71 |
| नीलम | 1.77 |
| हीरा | 2.42 |
सारणी 9.3 से नोट कीजिए कि यह आवश्यक नहीं कि प्रकाशिक सघन माध्यम का द्रव्यमान घनत्व भी अधिक हो, उदाहरण के लिए- किरोसिन जिसका अपवर्तनांक जल से अधिक है, जल की अपेक्षा प्रकाशिक सघन है, यद्यपि इसका द्रव्यमान घनत्व जल से कम है।
9.3.3 गोलीय लेंसों द्वारा अपवर्तन
आपने किसी घड़ीसाज़ को बहुत छोटे पुरुत्रों को देखने के लिए छोटे आवर्धक लेंस का उपयोग करते देखा होगा। क्या कभी आपने आवर्धक लेंस के पृष्ठ को अपने हाथों से छूकर देखा है? क्या इसका पृष्ठ समतल है या वक्रित है? क्या यह बीच से मोटा है या किनारों से? चश्मों में हम लेंसों का ही उपयोग करते हैं। घड़ीसाज़ के आवर्धक में भी लेंस लगा होता है। लेंस क्या है? यह प्रकाश किरणों को किस प्रकार मोड़ता है? इस अनुच्छेद में हम इसी विषय में अध्ययन करेंगे।
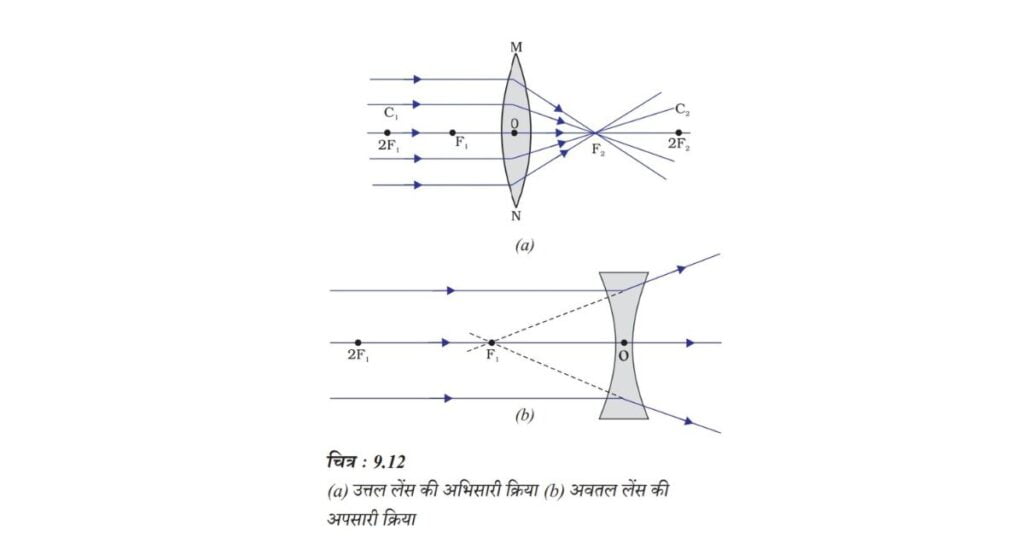
दो पृष्ठों से घिरा हुआ कोई पारदर्शी माध्यम, जिसका एक या दोनों पृष्ठ गोलीय हैं, लेंस कहलाता है। इसका अर्थ यह है कि लेंस का कम-से-कम एक पृष्ठ गोलीय होता है। ऐसे लेसा में दूसरा पृष्ठ समतल हा सकता है। किसी लेंस में बाहर की ओर उभरे दो गोलीय पृष्ठ हो सकते हैं। ऐसे लेंस को द्वि-उत्तल लेंस कहते हैं। इसे केवल उत्तल लेंस भी कहते हैं। यह किनारों की अपेक्षा बीच से मोटा होता है। उत्तल लेंस प्रकाश किरणों का चित्र 9.12 (a) में दर्शाए अनुसार अभिसरित करता है। इसीलिए उत्तल लेंसों को अभिसारी लेंस भी कहते हैं। इसी प्रकार एक द्वि-अवतल लेंस अंदर की ओर वक्रित दो गोलीय पृष्ठों से घिरा होता है। यह बीच की अपेक्षा किनारों से मोटा होता है। ऐसे लेंस प्रकाश किरणों को चित्र 9.12 (b) में दर्शाए अनुसार अपसरित करते हैं। ऐसे लेंसों को अपसारी लेंस कहते हैं। द्वि-अवतल लेंस प्रायः अवतल लेंस भी कहलाता है।
किसी लेंस में चाहे वह उत्तल हो अथवा अवतल, दो गोलीय पृष्ठ होते हैं। इनमें से प्रत्येक पृष्ठ एक गोले का भाग होता है। इन गोलों के केंद्र लेंस के वक्रता केंद्र कहलाते हैं। लेंस का वक्रता केंद्र प्रायः अक्षर C द्वारा निरूपित किया जाता है, क्योंकि लेंस के दो वक्रता केंद्र हैं। इसलिए, इन्हें। C तथा C द्वारा निरूपित किया जाता 2 है। किसी लेंस के दोनों वक्रता केंद्रों से गुजरने वाली एक काल्पनिक सीधी रेखा लेंस का मुख्य अक्ष कहलाती है। लेंस का केंद्रीय बिंदु इसका प्रकाशिक केंद्र कहलाता है। इसे प्रायः अक्षर O से निरूपित करते हैं। लेस के प्रकाशिक केंद्र से गुजरने वाली प्रकाश किरण बिना किसी विचलन के निर्गत होती है। गोलीय लेंस की वृत्ताकार रूपरेखा का प्रभावी व्यास इसका द्वारक (aperture) कहलाता है। इस अध्याय में अपने विवेचन में हम केवल उन्हीं लेंसों तक सीमित रहेंगे, जिनका द्वारक इनकी वक्रता त्रिज्या से बहुत छोटा है और दोनों वक्रता केंद्र प्रकाशिक केंद्र से समान ट्री पर होते हैं। ऐसे लेंस छोटे द्वारक के पतले लेंस कहलाते हैं। जब किसी लेंस पर समांतर किरणें आपतित होती हैं तो क्या होता है? इसे समझने के लिए आइए, एक क्रियाकलाप करें।
क्रियाकलाप 9.11
चेतावनी- इस क्रियाकलाप को करते समय अथवा अन्यथा भी सूर्य की ओर सीधे या लेंस से न देखें। यदि आप ऐसा करेंगे तो आपकी आँखों को क्षति हो सकती है।
• एक उत्तल लेंस को अपने हाथ में पकड़िए। इसे सूर्य की ओर निर्दिष्ट कीजिए।
• सूर्य के प्रकाश को एक कागज़ की शीट पर फोकसित कीजिए। सूर्य का एक तीक्ष्ण चमकदार प्रतिबिंब प्राप्त कीजिए।
• कागज तथा लेंस को कुछ समय के लिए उसी स्थिति में पकड़े रखिए। कागज को देखते रहिए। क्या होता है? ऐसा क्यों होता है? क्रियाकलाप 9.2 के अपने अनुभवों को स्मरण कीजिए।
कागज सुलगने लगता है और धुआँ उत्पन्न होता है। कुछ समय पश्चात यह आग भी पकड़ सकता है। ऐसा क्यों होता है? सूर्य से आने वाली प्रकाश की किरणें समानांतर होती हैं। लेंस द्वारा यह किरणें एक तीक्ष्ण चमकदार बिंदु के रूप में कागज पर अभिकेंद्रित कर दी जाती हैं। वास्तव में, कागज की शीट पर यह चमकदार बिंदु सूर्य का प्रतिबिंब है। एक बिंदु पर सूर्य के प्रकाश का संकेंद्रण ऊष्मा उत्पन्न करता है। इसके कारण कागज जलने लगता है।
अब हम एक लेंस के मुख्य अक्ष के समानांतर प्रकाश किरणों पर विचार करते हैं। जब आप प्रकाश की ऐसी किरणों को किसी लेंस से गुज़ारते हैं तो क्या होता है? एक उत्तल लेंस के लिए इसे चित्र 9.12 (a) में तथा अवतल लेंस के लिए चित्र 9.12 (b) में दर्शाया गया है।
चित्र 9.12 (a) को ध्यानपूर्वक देखिए। उत्तल लेंस पर मुख्य अक्ष के समानांतर प्रकाश की बहुत सी किरणें आपतित हैं। ये किरणें लेंस से अपवर्तन के पश्चात मुख्य अक्ष पर एक बिंदु पर अभिसरित हो जाती हैं। मुख्य अक्ष पर यह बिंदु लेंस का मुख्य फोकस कहलाता है। आइए, अब एक अवतल लेंस का व्यवहार देखें।
चित्र 9.12 (b) को ध्यानपूर्वक देखिए। अवतल लेंस पर मुख्य अक्ष के समानांतर प्रकाश की अनेक किरणें आपतित हो रही हैं। ये किरणें लेंस से अपवर्तन के पश्चात मुख्य अक्ष के एक बिंदु से अपसरित होती प्रतीत होती हैं। मुख्य अक्ष पर यह बिंदु अवतल लेंस का मुख्य फोकस कहलाता है।
यदि आप किसी लेंस के विपरीत पृष्ठ से समांतर किरणों को गुजरने दें तो आपको पहले से विपरीत दिशा में दूसरा मुख्य फोकस प्राप्त होगा। मुख्य फोकस को निरूपित करने के लिए प्रायः अक्षर F का प्रयोग होता है। तथापि, किसी लेंस में दो मुख्य फोकस होते हैं। इन्हें FI तथा F2 द्वारा निरूपित किया जाता है। किसी लेंस के मुख्य फोकस की प्रकाशिक केंद्र से दूरी फोकस दूरी कहलाती है। फोकस दूरी को अक्षर’ f’ द्वारा निरूपित किया जाता है। आप किसी उत्तल लेंस की फोकस दरी किस प्रकार ज्ञात कर सकत है? क्रियाकलाप 9.1। को स्मरण कीजिए। इस क्रियाकलाप में लेंस की स्थिति तथा सूर्य के प्रतिबिब की स्थिति के बीच की दूरी लेंस की सन्निकट (लगभग) फोकस दूरी बताती है।
9.3.4 लेंसों द्वारा प्रतिबिंब बनना
लेंस प्रतिबिंब कैसे बनाते हैं? लेंस प्रकाश के अपवर्तन द्वारा प्रतिबिब बनाते हैं। उन प्रतिबिंबों की प्रकृति क्या है? आइए, पहले उत्तल लेंस के लिए इसका अध्ययन करें।
क्रियाकलाप 9.12
• एक उत्तल लेंस लीजिए । क्रियाकलाप 9.11 में वर्णित विधि द्वारा इसकी सन्निकट फोकस दूरी ज्ञात कीजिए।
• एक लंबी मेज़ पर चॉक का प्रयोग करके पाँच समानांतर सीधी रेखाएँ, इस प्रकार खींचिए कि किन्हीं दो उत्तरोतर रेखाओं के बीच की दूरी लेंस की फोकस दूरी के बराबर हो।
• लेंस को एक लेंस स्टैंड पर लगाइए। इसे मध्य रेखा पर इस प्रकार रखिए कि लेंस का प्रकाशिक केंद्र इस रेखा पर स्थित हो।
• लेंस के दोनों ओर दो रेखाएँ क्रमशः लेंस के F तथा 2F के तदनुरूपी होंगी। इन्हें उचित अक्षरों द्वारा अंकित कीजिए, जैसे- क्रमशः 2 F1, F1, F2 तथा 2 F2।
• एक जलती हुई मोमबत्ती को बाई ओर, 2F1 से काफ़ी दूर रखिए। लेंस के विपरीत दिशा में रखे एक परदे पर इसका स्पष्ट एवं तीक्ष्ण प्रतिबिंब बनाइए।
• प्रतिबिंब की प्रकृति, स्थिति तथा आपेक्षिक साइज नोट कीजिए।
• इस क्रियाकलाप में बिंब को 2F1 से थोड़ा दूर, F1तथा 2F1 के बीच, F1 पर तथा F, और O के बीच रख कर दोहरावणं अपन प्रेक्षणों को नोट कीजिए तथा सारणीबद्ध कीजिए।
बिंब की विभिन्न स्थितियों के लिए उत्तल लेंस द्वारा बनाए गए प्रतिबिंब की प्रकृति, स्थिति तथा आपेक्षिक साइज का संक्षिप्त विवरण सारणी 9.4 में दिया गया है।
सारणी 9.4 बिब की विभिन्न स्थितियों के लिए उत्तल लेंस द्वारा बने प्रतिबिंब की प्रकृति, स्थिति तथा आपेक्षिक साइन

आइए, अब किसी अवतल लेंस द्वारा बने प्रतिबिंब की प्रकृति, स्थिति तथा आपेक्षिक साइज़ का एक क्रियाकलाप द्वारा अध्ययन करें।
क्रियाकलाप 9.13
• एक अवतल लेंस लीजिए। इसे एक लेंस स्टैंड पर रखिए।
• लेंस के एक ओर एक जलती हुई मोमबत्ती को रखिए।
• लेंस के दूसरी ओर से प्रतिबिंब का प्रेक्षण कीजिए। प्रतिबिंब को यदि संभव हो तो परदे पर प्राप्त करने का प्रयत्न कीजिए। यदि ऐसा संभव न हो तो प्रतिबिंब को लेंस में से सीधे ही देखिए।
• प्रतिबिंब की प्रकृति, आपेक्षिक साइज़ तथा सन्निकट स्थिति नोट कीजिए। मोमबत्ती को लेंस से दूर ले जाइए। प्रतिबिंब के साइज में परिवर्तन नोट कीजिए। जब
• मोमबत्ती को लेंस से बहुत दूर रखा जाता है तो प्रतिबिंब के साइज़ पर क्या प्रभाव पड़ता है?
उपरोक्त क्रियाकलाप का संक्षिप्त विवरण सारणी 9.5 में दिया गया है।
सारणी 9.5 बिंब की विभिन्न स्थितियों के लिए अवतल लेंस द्वारा बने प्रतिबिंब की प्रकृति, स्थिति तथा आपक्षिक साइज
| बिंब की स्थिति | प्रतिबिंब की स्थिति | प्रतिबिंब का आपेक्षिक साइज | प्रतिबिंध की प्रकृति |
| अनंत पर | फोकस F1 पर | अत्यधिक छोटा,बिंदु आकार छोटा | आभासी तथा सीधा |
| अनंत तथा लेंस के प्रकाशिक केंद्र O | फोकस F1 तथा प्रकाशिक O केंद्र के बीच | आभासी तथा सीधा |
इस क्रियाकलाप से आप क्या निष्कर्ष निकालते हैं? अवतल लेंस सदैव एक आभासी, सीधा तथा छोटा प्रतिबिंब चनाएगा, चाहे बिंब कहीं भी स्थित हो।
9.3.5 किरण आरेखों के उपयोग द्वारा लेंसों से प्रतिबिंब बनना
हम किरण आरेर्खा के उपयोग द्वारा लेंसों से प्रतिबिंबों के बनने को निरूपित कर सकते हैं। किरण आरेख लेंसों में बने प्रतिबिंबों की प्रकृति, स्थिति तथा आपेक्षिक साइज़ का अध्ययन करने में भी हमारी सहायता करेंगे। लेंसों में किरण आरेख बनाने के लिए गोलीय दर्पणों की भाँति हम निम्नलिखित में से किन्हीं दो किरणों पर विचार कर सकते हैं।
(i) बिंब से, मुख्य अक्ष के समानांतर आने वाली कोई प्रकाश किरण उत्तल लेंस से अपवर्तन के पश्चात चित्र 9.13 (a) में दर्शाए अनुसार लेंस के दूसरी ओर मुख्य फोकस से गुज़रेगी। अवतल लेंस की स्थिति में प्रकाश किरण चित्र 9.13
(b) में दर्शाए अनुसार लेंस के उसी ओर स्थित मुख्य फोकस से अपसरित होती प्रतीत होती है।

(ii) मुख्य फोकस से गुज़रने वाली प्रकाश किरण, उत्तल लेंस से अपवर्तन के पश्चात मुख्य अक्ष के समानांतर निर्गत होगी। इसे चित्र 9.14 (a) में दर्शाया गया है। अवतल लेंस के मुख्य फोकस पर मिलती प्रतीत होने वाली प्रकाश किरण, अपवर्तन के पश्चात मुख्य अक्ष के समानांतर निर्गत होगी। इसे चित्र 9.14 (b) में दर्शाया गया है।

(iii) लेंस के प्रकाशिक केंद्र र से गुजरने वाली प्रकाश किरण अपवर्तन के पश्चात बिना किसी विचलन के निर्गत होती है। इसे चित्र 9.15 (a) तथा 9.15 (b) में दर्शाया गया है।

चित्र 9.16 में उत्तल लेंस द्वारा किसी बिंब की कुछ स्थितियों में, प्रतिबिंब बनने को किरण आरेखों द्वारा दर्शाया गया है। चित्र 9.17 में अवतल लेंस द्वारा बिंब की विभिन्न स्थितियों में प्रतिबिंब बनने को किरण आरेखों द्वारा दर्शाया गया है।




9.3.6 गोलीय लेंसों के लिए चिह्न-परिपाटी
लेंसों के लिए, हम गोलीय दर्पणों जैसी ही चिह्न-परिपाटी अपनाएँगे। दूरियों के चिह्नों के निर्धारण के लिए हम यहाँ भी उन्हीं नियमों को अपनाएँगे। केवल, जहाँ दर्पणों में सभी दूरियाँ उनके ध्रुवों से नापी जाती हैं वहाँ लेंसों में सभी माप उनके प्रकाशिक केंद्र से लिए जाते हैं। परिपाटी के अनुसार उत्तल लेंस की फोकस दूरी धनात्मक होती है, जबकि अवतल लेंस की फोकस दूरी ऋणात्मक होती है। आपको u, v तथा f, बिंब ऊँचाई । तथा प्रतिबिंब ऊँचाई ॥’ के मान में उचित चिह्नों का चयन करने में सावधानी बरतनी चाहिए।
9.3.7 लेंस सूत्र तथा आवर्धन
जिस प्रकार हमने गोलीय दर्पणों के लिए सूत्र ज्ञात किया था, उसी प्रकार गोलीय लेंसों के लिए भी लेंस सूत्र स्थापित किया गया है। यह सूत्र बिंब दूरी (५), प्रतिबिंब दूरी (४) तथा फोकस दूरी (1) के बीच संबंध प्रदान करता है। लेंस सूत्र व्यक्त किया जाता है-
(1/v) – (1/u) = 1/f (9.8)
उपरोक्त लेंस सूत्र व्यापक हे तथा किसी भी गोलीय लंस के लिए, सभी स्थितियों में मान्य है। लेसों से संबंधित प्रश्नों को हल करने के लिए लस सूत्र में आंकिक मान प्रतिस्थापित करत समय विभिन्न राशियों के उचित चिह्नां का ध्यान रखना चाहिए।
आवर्धन
किसी लेंस द्वारा उत्पन्न आवर्धन, किसी गोलीय दर्पण द्वारा उत्पन्न आवर्धन की ही भाँति प्रतिबिंब की ऊँचाई तथा बिंब की ऊँचाई के अनुपात के रूप में परिभाषित किया जाता है। आवर्धन को अक्षर द्वारा निरूपित किया जाता है। यदि बिंब की ऊँचाई । हो तथा लेंस द्वारा बनाए गए प्रतिबिंच की ऊँचाई ।’ हो, तब लेंस द्वारा उत्पन्न आवर्धन प्राप्त होगा-
m = प्रतिबिब की ऊंचाई / बिंब की ऊँचाई = h’/h (9.9)
लेंस द्वारा उत्पन्न आवर्धन, बिंब दूरी तथा प्रतिबिंब दूरी से भी संबंधित है। इस संबंध को व्यक्त करते हैं-
आवर्धन (m) = h’/h = v/u (9.10)
उदाहरणा 9.3 किसी अवतल लेंस की फोकस दरी 15 cm है। बिंब को लेंस से कितनी दूरी पर रखें कि इसके द्वारा बिंब का लेंस से 10 cm दूरी पर प्रतिबिंब बने? लेंस द्वारा उत्पन्न आवर्धन भी ज्ञात कीजिए।
हल:
अवतल लेंस द्वारा सदैव ही आभासी, सीधा प्रतिबिंब उसी ओर बनता है, जिस ओर बिंब रखा होता है।
प्रतिबिंब-दूरी v = -10 cm
फोकस दूरी f = -15 cm
बिंब-दूरी u = ?
क्योंकि 1/u – 1/v = 1/f
या 1/u = (1/v) – (1/f)
1/u = 1/(-10) – 1/(-15)
= -1/10 + 1/15
1/u = -3+2/30 = 1/(-30)
u = – 30cm
इसी प्रकार बिंब की दूरी 30 cm है।,
आवर्धन, m= v/h
m = -10/-30 = 1/3 = 0.33
यहाँ धनात्मक चिह्न यह दर्शाता है कि प्रतिबिंब सीधा तथा आभासी है। प्रतिबिंब का साइज़ बिंब के साइज़ का एक-तिहाई है।
उदाहरण 9.4 कोई 2.0 cm लंबा बिंब 10 cm फोकस दूरी के किसी उत्तल लेंस के मुख्य अक्ष के लंबवत रखा है। बिंब की लेंस से दूरी 15 cm है। प्रतिबिंब की प्रकृति, स्थिति तथा साइज ज्ञात कीजिए। इसका आवर्धन भी ज्ञात कीजिए।
हल:
बिंब की ऊँचाई h = +2.0 cm
फोकस दूरी f = +10 cm
बिंब-दूरी ॥ = -15 cm
प्रतिबिंब-दूरी v = ?
प्रतिबिंब की ऊँचाई h’ =?
क्योंकि 1/v-1/u = 1/f
या 1/v = 1/u + 1/f
1/v = 1/(-15) + 1/10
1/v = -2+3/30
1/v = 1/30
u = + 30 cm
v का धनात्मक चिह्न यह दर्शाता है कि प्रतिबिंब लेंस के प्रकाशिक केंद्र के दाईं ओर 30 cm दूरी पर बनता है। प्रतिबिंब वास्तविक तथा उलटा है।
आवर्धन, m = h’/h = v/u
अथवा h’ = h (u/v)
प्रतिबिंब की ऊँचाई h’ = (2.0){ +30/-15} = -4.0 cm
आवर्धन m = + 30/-15cm = -2
m तथा h’ के ऋणात्मक चिह्न यह दर्शाते हैं कि उपरोक्त वर्णन के अनुसार प्रतिबिंब उलटा तथा वास्तविक है। यह मुख्य अक्ष के नीचे बनता है। इस प्रकार एक वास्तविक उलटा तथा 4.0 cm लंबा प्रतिबिंब लेंस के दाईं ओर लेंस से 30 cm दूरी पर बनता है। यह प्रतिबिंब दोगुना विवर्धित है।
9.3.8 लेंस की क्षमता
आप जानते हैं कि किसी लेंस की प्रकाश किरणों को अभिसरित अथवा अपसरित करने की क्षमता उसकी फोकस दूरी पर निर्भर करती है, उदाहरण के लिए- कम फोकस दूरी का एक उत्तल लेंस प्रकाश किरणों को बड़े कोण से मोड़कर उन्हें प्रकाशिक केंद्र के निकट फोकसित कर देता है। इसी प्रकार, कम फोकस दूरी का एक अवतल लेंस अधिक फोकस दूरी के लेंस की अपेक्षा प्रकाश किरणों को अधिक अपसरित करता है। किसी लेंस द्वारा प्रकाश किरणों को अभिसरण या अपसरण करने की मात्रा (degree) को उसकी क्षमता के रूप में व्यक्त किया जाता है। इसे अक्षर P द्वारा निरूपित करते हैं। किसी / फोकस दूरी के लेंस की क्षमता,
P = 1/f (9.11)
लेंस की क्षमता का SI मात्रक ‘डाइऑप्टर’ है। इसे अक्षर D द्वारा दर्शाया जाता है। यदि को मीटर में व्यक्त करें तो क्षमता को डाइऑप्टर में व्यक्त किया जाता है। इस प्रकार, 1 डाइऑप्टर उस लेंस की क्षमता है, जिसकी फोकस दूरी 1 मीटर हो। 1D = 1m-1 । आप नोट कर सकते हैं कि उत्तल लेंस की क्षमता धनात्मक तथा अवतल लेंस की क्षमता ऋणात्मक होती है।
चश्मा बनाने वाले जब संशोधी लेंस निर्धारित करते हैं तो उनकी क्षमता का उल्लेख करते हैं। मान लीजिए निर्धारित लेंस की क्षमता + 2.0 D है। इसका अर्थ है कि निर्धारित लेंस उत्तल है और उसकी फोकस दूरी + 0.50 m है। इसी प्रकार, -2.5 D क्षमता के लेंस की फोकस दूरी -0.40 m होती है। यह लेंस अवतल होता है।
आपने क्या सीखा
• प्रकाश सरल रेखाओं में गमन करता प्रतीत होता है।
• दर्पण तथा लेंस वस्तुओं के प्रतिबिंब बनाते हैं। बिंब की स्थिति के अनुसार प्रतिबिंब वास्तविक अथवा आभासी हो सकते हैं।
• सभी प्रकार के परावर्ती पृष्ठ परावर्तन के नियमों का पालन करते हैं। अपवर्ती पृष्ठ अपवर्तन के नियमों का पालन करते हैं।
• गोलीय दर्पणों तथा लेंसों के लिए नई कार्तीय चिह्न-परिपाटी अपनाई जाती है।
• दर्पण सूत्र दर्पण सूत्र (1/v) + (1/u) = 1/f बिंब-दूरी (u), प्रतिबिंब-दूरी (v) तथा गोलीय दर्पण की फोकस दूरी (f) में संबंध दर्शाता है।
• किसी गोलीय दर्पण की फोकस दूरी उसकी वक्रता त्रिज्या की आधी होती है।
• किसी गोलीय दर्पण द्वारा उत्पन्न आवर्धन, प्रतिबिंब की ऊँचाई तथा बिंब की ऊँचाई का अनुपात होता है।
• सघन माध्यम से विरल माध्यम में तिरछी गमन करने वाली कोई प्रकाश किरण अभिलंब से परे झुक जाती है। विरल माध्यम से सघन माध्यम में तिरछी गमन करने वाली प्रकाश किरण अभिलंब की ओर झुक जाती है।
• निर्वात में प्रकाश 3 × 108m /s की अत्यधिक चाल से गमन करता है। विभिन्न माध्यमों में प्रकाश की चाल भिन्न-भिन्न होती है।
• किसी पारदर्शी माध्यम का अपवर्तनांक प्रकाश की निर्वात में चाल तथा प्रकाश होता है। की माध्यम में चाल का अनुपात
• किसी आयताकार काँच के स्लैब के प्रकरण में, अपवर्तन वायु-काँच अंतरापृष्ठ एवं काँच-वायु अंतरापृष्ठ दोनों पर होता है। निर्गत किरण आपतित किरण की दिशा के समांतर होती है।
• लेंस सूत्र : (1/v) + (1/u) = 1/f बिंव-दूरी (u), प्रतिविव-दूरी (v) त ) तथा गोलीय लेंस की फोकस दूरी (f) में संबंध दर्शाता है।
• किसी लेस की क्षमता आकी फोकस दूरी का व्युत्क्रम होती है। लेस की क्षमता का SI मात्रक डाइऑप्टर है।
यह भी पढ़ें : आनुवांशिकता : अध्याय 8
अभ्यास
1. निम्न में से कौन-सा पदार्थ लेस बनाने के लिए प्रयक्त नहीं किया जा सकता?
(a) जल
(b) काँच
(c) प्लास्टिक
(d) मिट्टीं
Ans. (d) मिट्टीं
2. किसी बिंव का अवतल दर्पण द्वारा बना प्रतिबिंब आभासी, सीधा तथा बिब से बड़ा पाया गया। वस्तु की स्थिति कहाँ होनी चाहिए?
(a) मुख्य फोकस तथा वक्रता केंद्र के बीच
(b) वक्रता केंद्र पर
(c) वक्रता केंद्र से परे
(d) दर्पण के ध्रुव तथा मुख्य फोकस के बीच
Ans. (d) दर्पण के ध्रुव तथा मुख्य फोकस के बीच
3. किसी बिंब का वास्तविक तथा समान साइन का प्रतिबिंब प्राप्त करने के लिए बिंब को उत्तल लेंस के सामने कहाँ रखें?
(a) लेंस के मुख्य फोकस पर
(b) फोकस दूरी की दोगुनी दूरी पर
(c) अनंत पर
(d) लेंस के प्रकाशिक केंद्र तथा मुख्य फोकस के बीच
Ans. (b) फोकस दूरी की दोगुनी दूरी पर
4. किसी गोलीय दर्पण तथा किसी पतले गोलीय लेंस दोनों की फोकस दूरियाँ -15 cm हैं। दर्पण तथा लेंस संभवतः है
(a) दोनों अवतल
(b) दोनों उत्तल
(c) दर्पण अवतल तथा लेंस उत्तल
(d) दर्पण उत्तल तथा लेंस अवतल
Ans. (a) दोनों अवतल
5. किसी दर्पण से आप चाहे कितनी ही दूरी पर खड़े हों, आपका प्रतिबिंब सदेव सीधा प्रतीत होता है। संभवतः दर्पण है-
(a) केवल समतल
(b) केवल अवतल
(c) केवल उत्तल
(d) या तो समतल अथवा उत्तल
Ans. (d) या तो समतल अथवा उत्तल
6. किसी शब्दकोष (dictionary) में पाए गए छोटे अक्षरों को पढ़ते समय आप निम्नलिखित में से कौन-सा लेंस पसंद करेंगे?
(a) 50 cm फोकस दूरी का एक उत्तल लेंस
(b) 50 cm फोकस दूरी का एक अवतल लेंस
(c) 5 cm फोकस दूरी का एक उत्तल लेंस
(d) 5 cm फोकस टूरी का एक अवत्तल जैस
Ans. (c) 5 cm फोकस दूरी का एक उत्तल लेंस
7. 15 cm फोकस दूरी के एक अवतल दर्पण का उपयोग करके हम किसी बिंब का सीधा प्रतिबिंब बनाना चाहते है। बिंब का दर्पण से दरी का परिसर (range) क्या होना चाहिए? प्रतिबिंब की प्रकृति कैसी है? प्रतिबिंब बिंब से बड़ा है अथवा छोटा? इस स्थिति में प्रतिबिंब बनने का एक किरण आरेख बनाइए।
Ans. अवतल दर्पण में आभासी एवं सीधा प्रतिबिंब तभी बनता है जब बिंब मुख्य फोकस और ध्रुव के बीच हो | चूँकि अवतल दर्पण का फोकस दुरी 15 cm है, अर्थात ध्रुव और फोकस की बीच की दुरी 15 cm है | इसलिए बिंब को 0cm से 15cm के बीच दर्पण के सामने रखना चाहिए, तभी सीधा प्रतिबिंब बनता है |

प्रतिबिंब की प्रकृति : आभासी एवं सीधा
प्रतिबिंब का आकार : वस्तु से बड़ा
8. निम्नलिखित स्थितियों में प्रयुक्त दर्पण का प्रकार बताइए-
(a) किसी कार का अग्र-दीप (हेड-लाइट)
Ans. किसी कार का अग्र-दीप (हैड-लाइट) अवतल दर्पण का बनाया जाता है, क्योंकि यदि बल्ब को दर्पण के मुख्य फोकस पर रख दिया जाए तो यह दर्पण से परावर्तित होकर एक समांतर किरण पुंज बनाता है |

(b) किसी वाहन का पार्श्व/पश्च-दृश्य दर्पण
Ans. किसी वाहन का पार्श्व/पश्च-दृश्य दर्पण के लिए उत्तल दर्पण का प्रयोग किया जाता है क्योंकि ये सदैव छोटा परन्तु सीधा प्रतिबिंब बनाता है | चूँकि उत्तल दर्पण बाहर की ओर वक्रित होता है इसलिए इसका दृष्टि-क्षेत्र काफी बढ़ जाता है जीससे ड्राईवर गाड़ी के पीछे के बहुत बड़े हिस्से को देख पाता है |
(c) सौर भट्टी अपने उत्तर की कारण सहित पुष्टि कीजिए।
Ans. सौर भट्टी में सूर्य के प्रकाश केन्द्रित करना पड़ता है जिसके लिए अवतल दर्पण उपयुक्त है | यह दर्पण अनंत से होकर आने वाला मुख्य अक्ष के समान्तर प्रकाश किरणों को फोकस से होकर गुजारता है जिससे फोकस के आस-पास का तापमान 180०C से 200०C तक बढ़ जाता है।
9. किसी उत्तल लेंस का आधा भाग काले कागज से ढक दिया गया है। क्या यह लेंस किसी बिंब का पूरा प्रतिबिंब बना पाएगा? अपने उत्तर की प्रयोग द्वारा जाँच कीजिए। अपने प्रेक्षणों की व्याख्या कीजिए।
Ans. हाँ, किसी उत्तल लेंस का आधा भाग काले कागज़ से ढक देने पर भी उत्तल लेंस दिए गए बिंब का पूरा प्रतिबिंब बनाता है। प्रायोगिक विधि द्वारा जाँच-सर्वप्रथम एक उत्तल लेंस लीजिए तथा इसके आधे भाग को काले कागज़ से ढक दीजिए। अब लेंस को किसी स्टैंड के सहारे दी गई आकृति के अनुसार रखिए। लेंस के एक तरफ़ जलती हुई मोमबत्ती तथा दूसरी तरफ़ एक सफ़ेद पर्दा रखिए। हम पाते हैं कि पर्दे पर मोमबत्ती का पूरा उल्टा प्रतिबिंब बनता है।

प्रेक्षण–
- प्रतिबिंब की संरचना लेंस के आकार पर निर्भर नहीं करती है, एक छोटा लेंस भी वस्तु का पूर्ण प्रतिबिंब बना सकता है।
- परंतु प्रतिबिंब की चमक (brightness) अपेक्षाकृत कम हो जाती है, क्योंकि लेंस से गुजरने वाली प्रकाश की किरणों की संख्या कम हो जाती है।
10. 5 cm लंबा कोई बिंब 10 cm फोकस दूरी के किसी अभिसारी लेंस से 25 cm दूरी पर रखा जाता है। प्रकाश किरण-आरेख खींचकर बनने वाले प्रतिबिंब की स्थिति, साइज तथा प्रकृति ज्ञात कीजिए।
Ans.

बिंब की ऊंचाई (h) = + 5cm
अभिसारी तथा उत्तर लेंस में
बिंब की दूरी = -25 cm
फोकस दूरी = + 10 cm (लेंस अभिसरी है)
लेंस सूत्र द्वारा
(1/v) – (1/u) = 1/f
(1/v) = (1/u) + 1/f
1/v = 1/10 + 1/25
v = 250/15
v = 16.67 cm
प्रतिबिंब की स्थिति : प्रतिबिंब लेंस के दूसरी ओर 16.67 cm की दुरी पर बनेगा।
प्रतिबिम्व की साइज़ m = (h’)/h = v/u
h’/5 = (50/3) / (-25)
h’/5 = 2/(-3)
h’ = 10/(-3)
h’ = – 3.33 cm
प्रतिबिंब का साइज: प्रतिबिंब बिंब से छोटा है। तथा ऋणात्मक चिन्ह बताता है कि प्रतिबिंच वास्तविक और उल्टा है। प्रतिविंव की प्रकृति: वास्तविक और उल्टा ।
11. 15 cm फोकस दूरी का कोई अवतल लेंस किसी बिंब का प्रतिबिंब लेंस से 10 cm दूरी पर बनाता है। बिंब लेंस से कितनी दूरी पर स्थित है? किरण आरेख खीचिए।
Ans.

अवतल लेंस की फोकस दूरी (f) = -15cm
बिंब की दूरी (u) = ?
प्रतिबिंब की दूरी (v) = -10cm
लेंस सूत्र द्वारा
(1/v) – (1/u) = 1/f
1/u = 1/v – 1/f
1/u = – 1/10 – 1/(-15)
1/u = – 1/10 + 1/15
1/u = -1/30
u = -30 cm
अतः बिंब को लेंस से 20cm दूर रखेंगे।
12. 15 cm फोकस दूरी के किसी उत्तल दर्पण से कोई बिंब 10 cm दूरी पर रखा है। प्रतिबिंब की स्थिति तथा प्रकृति ज्ञात कीजिए।
Ans. उत्तल दर्पण की फोकस दूरी = -15 cm
बिंब की दूरी = -10 cm
अतः दर्पण सूत्र द्वारा
(1/v) + (1/u) = 1/f
(1/v) = 1/f – (1/u)
(1/v) = 1/15 – 1/(-10)
1/v = 1/15 + 1/10
1/v = 25/150
v = 6cm
अतः प्रतिबिम्ब दर्पण के पीछे 6 cm की दूरी पर बनेगा तथा यह एक आभासी तथा सीधा होगा।
13. एक समतल दर्पण द्वारा उत्पन्न आवर्धन +1 है। इसका क्या अर्थ है?
Ans. समतल दर्पण द्वारा उत्पन्न आवर्धन 1 है इसका अर्थ यह है कि बिंब का आकार प्रतिबिंब के आकार के बराबर है और बिंब से समान दुरी पर प्रतिबिंब दर्पण के पीछे बना है | इसका धनात्मक चिन्ह यह बताता है कि प्रतिबिंब आभासी और सीधा है |
14. 5.0 cm लंबाई का कोई बिंब 30 cm वक्रता त्रिज्या के किसी उत्तल दर्पण के सामने 20 cm दूरी पर रखा गया है। प्रतिबिंब की स्थिति, प्रकृति तथा साइज ज्ञात कीजिए।
Ans.
उत्तल दर्पण की वक्रता त्रिज्या (R) = 30cm
दर्पण की फोकस दूरी (f) = R/2
दर्पण से बिंब की दूरी (u) = -20cm
बिंब का आकार/ऊँचाई (h) = 5.0cm
प्रतिबिंब की दूरी (v) = ? प्रतिबिंब का आकार (h’) = ?
दर्पण सूत्र द्वारा
(1/v) + (1/u) = 1/f
1/v = 1/f – 1/h
1/v = 1/15 + 1/20
1/v = (4+3)/60
v = 8.57 cm
प्रतिबिंब की स्थिति : प्रतिबिंब दर्पण के पीछे 8.57 cm दुरी पर बनेगा ।
प्रतिबिंब की प्रकृति : आभासी और सीधा होगा ।
साइज : m = h’/h = -v/u
= h’/5 = -(60/7)/-20
h’/5 = 3/7
h’ = 15/7 = 2.14 cm
अतः प्रतिबिंब बिंब से छोटा बनेगा ।
अतः प्रतिबिंब आभासी, सीधा तथा आकार में 2.14cm होगा।
15. 7.0 cm साइज़ का कोई बिंब 18 cm फोकस दूरी के किसी अवतल दर्पण के सामने 27 cm दूरी पर रखा गया है। दर्पण से कितनी दूरी पर किसी परदे को रखें कि आस पर वस्तु का स्पष्ट फोकसित प्रतिविव प्राप्त किया जा सके। प्रतिबिंब का साइज तथा प्रकृति ज्ञात कीजिए।
Ans. अवतल दर्पण की फोकस दुरी (f) = -18 cm
बिंब की दुरी (u) = -27 cm
बिंब की ऊंचाई (h) = 7 cm
दर्पण सूत्र द्वारा
(1/v) + (1/u) = 1/f
1/v = 1/f – 1/u
1/v = 1/(-18) – 1/(-27)
1/v = -1/18 + 1/27
1/v = -3+2/54
1/v = -1/54
v = -54 cm
प्रतिबिंब की स्थिति : प्रतिबिंब दर्पण के सामने 54 cm दुरी पर बनेगा |
प्रकृति : वास्तविक और उल्टा होगा।
प्रतिबिंब का साइज़ m = h’/h = -v/u
h’/7 = – (-54)/(-27)
h’/7 = -2
h’ = -14 cm
∴ प्रतिबिंब का साइज़ 14cm है जो बिंब से आवर्धित (बड़ा) है।
प्रतिबिंब की प्रकृति- चूँकि का मान ऋणात्मक है, इसलिए प्रतिबिंब वास्तविक तथा उल्टा है।
16. उस लेंस की फोकस दूरी ज्ञात कीजिए, जिसकी क्षमता 2.0 D है। यह किस प्रकार का लेंस है?
Ans. लेंस की क्षमता
P =1/f
f = 1/P
P = – 2
∴ f = 1/(-2) = 0.5 m = -50cm
लेंस की फोकस दूरी -50 cm है। इसलिए यह एक अपसारी (वायु में अवतल) लेंस है।
चूँकि लेंस की क्षमता और फोकस दूरी का मान ऋणात्मक है, इसलिए यह एक अवतल लेंस या अपसारी लेंस (concave lens) है।
17. कोई डॉक्टर +1.5 D. क्षमता का संशोधक लेंस निर्धारित करता है। लेस की फोकस दूरी ज्ञात कीजिए। क्या निर्धारित लेंस अभिसारी है अथवा अपसारी?
Ans. लेंस की क्षमता
P =1/f
f = 1/P
P = +1.5 D
∴ f = 1/(1.5) = 0.67 m = 67cm
चूँकि लेंस की क्षमता एवं फोकस दूरी के मान धनात्मक हैं अत: यह एक उत्तल लेंस (अभिसारी) लेंस है।

1 thought on “प्रकाश परावर्तन तथा अपवर्तन : अध्याय 9”